 ), car elle est une application de torsion nulle (i.e.
), car elle est une application de torsion nulle (i.e. 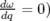 . Pour
appliquer le théorème KAM, il faut construire une forme normale d’ordre 2. En notations complexes, l’application
d’Hénon 2.76 s’exprime sous la forme :
. Pour
appliquer le théorème KAM, il faut construire une forme normale d’ordre 2. En notations complexes, l’application
d’Hénon 2.76 s’exprime sous la forme :  , où
, où  est la notation pour le complexe
conjugué de
est la notation pour le complexe
conjugué de  . Succinctement, on effectue un changement de variables
. Succinctement, on effectue un changement de variables  . Dans la nouvelle variable, la forme
normale d’ordre deux s’écrit comme une rotation dépendant de la distance à l’origine
. Dans la nouvelle variable, la forme
normale d’ordre deux s’écrit comme une rotation dépendant de la distance à l’origine  (Bazzani, Todesco,
Turchetti et Servizi, 1994, p. 96 sqq.) :
(Bazzani, Todesco,
Turchetti et Servizi, 1994, p. 96 sqq.) : ![ζ′ = exp(jΩ(ζ¯ζ))ζ avec Ω(ζ¯ζ) = ω − 1-[3cot ω-+ cot 3ω]ζ¯ζ
16 2 2](these924x.png) .
Le deuxième terme de
.
Le deuxième terme de  est bien non nul et correspond à la torsion de la forme normale d’ordre 2.
est bien non nul et correspond à la torsion de la forme normale d’ordre 2.