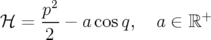
Avant d’appliquer l’Analyse en Fréquence à l’étude de la dynamique des accélérateurs, deux applications simples vont être présentées succinctement. Le pendule mécanique qui modélise la dynamique au voisinage d’une résonance. Puis, l’application d’Hénon qui est une application nonlinéaire et me permettra d’introduire quelques notions supplémentaires sur l’étude de la dynamique des systèmes.
Le Hamiltonien d’un pendule rigide peut s’écrire sous la forme :
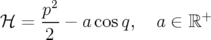 | (2.71) |
où  est l’angle de rotation du pendule et
est l’angle de rotation du pendule et  sa dérivée temporelle. Le pendule est un système
dynamique à un degré de liberté complètement intégrable qui permet de modéliser la dynamique
au voisinage d’une résonance (voir par exemple, Chirikov, 1979). Son portrait de phase
sa dérivée temporelle. Le pendule est un système
dynamique à un degré de liberté complètement intégrable qui permet de modéliser la dynamique
au voisinage d’une résonance (voir par exemple, Chirikov, 1979). Son portrait de phase  est
tracé pour différentes valeurs de l’énergie (Fig. 2.12-a). Deux régimes peuvent être mis en
évidence :
est
tracé pour différentes valeurs de l’énergie (Fig. 2.12-a). Deux régimes peuvent être mis en
évidence :
 ) où le pendule effectue des oscillations autour de l’origine de
période :
) où le pendule effectue des oscillations autour de l’origine de
période :
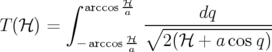 | (2.72) |
 ) est assez grande pour lui permettre
d’effectuer des mouvements de rotation de période :
) est assez grande pour lui permettre
d’effectuer des mouvements de rotation de période :
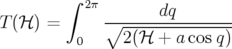 | (2.73) |
Le pendule admet deux points fixes correspondant aux positions d’équilibre stable et instable :
l’origine  est un point fixe elliptique et
est un point fixe elliptique et  est un point fixe
hyperbolique.
est un point fixe
hyperbolique.
La courbe en fréquence  est tracée pour
est tracée pour  , i.e. passant par le point
hyperbolique et y admet une singularité logarithmique. La période de rotation (Eq. 2.73) est alors
(voir par exemple Tabor, 1988 p. 11 sqq. et Laskar, 1993) :
, i.e. passant par le point
hyperbolique et y admet une singularité logarithmique. La période de rotation (Eq. 2.73) est alors
(voir par exemple Tabor, 1988 p. 11 sqq. et Laskar, 1993) :
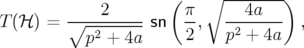 | (2.74) |
avec  , la fonction sinus elliptique de Jacobi :
, la fonction sinus elliptique de Jacobi :
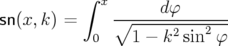 | (2.75) |
La courbe en fréquence 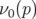 calculée pour
calculée pour  est identiquement nulle pour
est identiquement nulle pour  , car
la fréquence de circulation est nulle. Par contre au-delà, elle vaut
, car
la fréquence de circulation est nulle. Par contre au-delà, elle vaut 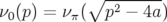 .
.
Ces deux courbes sont fondamentales, car elles décrivent le comportement de l’application
fréquence au voisinage d’une résonance (Laskar, 1993). La courbe  décrit son comportement
lorsqu’un point hyperbolique est traversé (Fig. 2.12-b), la courbe
décrit son comportement
lorsqu’un point hyperbolique est traversé (Fig. 2.12-b), la courbe 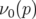 lorsqu’une île de
résonance est traversée (Fig. 2.12-c). Si l’on projette la courbe
lorsqu’une île de
résonance est traversée (Fig. 2.12-c). Si l’on projette la courbe 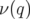 sur l’axe des fréquences, pour
un échantillonnage uniforme en
sur l’axe des fréquences, pour
un échantillonnage uniforme en 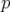 , l’allure de la courbe en fréquence ne dépend pas du
choix de
, l’allure de la courbe en fréquence ne dépend pas du
choix de 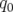 dans le régime libration (cf. courbes 2.12-d et 2.12-e et propriété (1) p. §).
Par contre l’échantillonnage est plus fin au voisinage de île de libration qu’au voisinage
du point hyperbolique, car la variation de la fréquence est plus rapide (cf. singularité
logarithmique).
dans le régime libration (cf. courbes 2.12-d et 2.12-e et propriété (1) p. §).
Par contre l’échantillonnage est plus fin au voisinage de île de libration qu’au voisinage
du point hyperbolique, car la variation de la fréquence est plus rapide (cf. singularité
logarithmique).
L’application d’Hénon (Hénon et Heiles, 1964 et Hénon, 1969) est la plus simple des applications non triviales symplectiques polynomiales à deux degrés de liberté (Bazzani et al., p. 77) :
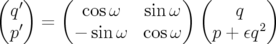 | (2.76) |
où 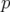 et
et  sont des variables canoniques et
sont des variables canoniques et 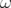 est le nombre de rotation. Elle dérive du
Hamiltonien dépendant explicitement du temps
est le nombre de rotation. Elle dérive du
Hamiltonien dépendant explicitement du temps  :
:
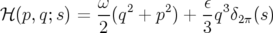 | (2.77) |
avec 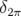 la fonction de Dirac
la fonction de Dirac 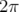 -périodisée.
-périodisée.
Malgré sa simplicité, l’application d’Hénon contient une grande partie de la dynamique
nonlinéaire que nous rencontrerons dans les chapitres suivants. La partie quadratique du
Hamiltonien 2.77 modélise le mouvement bétatron perturbé par un hexapôle situé en  (cf.
Wiedemann, Tome II ou Lee, 1998). Je ne l’introduis ici que pédagogiquement pour illustrer les
propriétés de l’application fréquence énoncées dans la section 2.2.3 et également pour discuter des
résonances induites par une perturbation de type hexapolaire (pour plus de détails, voir le travail de
Bazzani, Todesco, Turchetti et Servizi, 1994).
(cf.
Wiedemann, Tome II ou Lee, 1998). Je ne l’introduis ici que pédagogiquement pour illustrer les
propriétés de l’application fréquence énoncées dans la section 2.2.3 et également pour discuter des
résonances induites par une perturbation de type hexapolaire (pour plus de détails, voir le travail de
Bazzani, Todesco, Turchetti et Servizi, 1994).
Dans ce cas, l’application fréquence est simplement définie par :
| FT : ℝ | → ℝ | ||
| q |  ν ν | (2.78) |
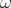 et pour un nombre d’itérations
et pour un nombre d’itérations  (Fig. 2.14) et
mettent respectivement en évidence des résonances d’ordre 4, 5, 6 et 7 (cf. grands îlots de
résonance). Pour chacun des cas, la courbe en fréquence
(Fig. 2.14) et
mettent respectivement en évidence des résonances d’ordre 4, 5, 6 et 7 (cf. grands îlots de
résonance). Pour chacun des cas, la courbe en fréquence 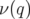 pour
pour  et
et  est adjointe. C’est une courbe monotone de l’amplitude
est adjointe. C’est une courbe monotone de l’amplitude  excepté au voisinage des
résonances. L’étude de la régularité de
excepté au voisinage des
résonances. L’étude de la régularité de 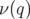 révèlent également des résonances d’ordre plus
élevé.
révèlent également des résonances d’ordre plus
élevé.
Similairement au cas du pendule, lorsque 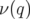 traverse une île, on observe un plateau, et au
voisinage d’un point hyperbolique une discontinuité de l’application fréquence. L’application
d’Hénon est suffisamment simple pour pouvoir calculer analytiquement la variation de
traverse une île, on observe un plateau, et au
voisinage d’un point hyperbolique une discontinuité de l’application fréquence. L’application
d’Hénon est suffisamment simple pour pouvoir calculer analytiquement la variation de  avec
avec  .
Pour cela, on écrit une forme normale de l’application d’Hénon au voisinage de l’origine qui est un
point fixe elliptique (voir Bazzani et al., 1994). Les largeurs de résonance peuvent aussi être
calculées et dépendent à la fois de
.
Pour cela, on écrit une forme normale de l’application d’Hénon au voisinage de l’origine qui est un
point fixe elliptique (voir Bazzani et al., 1994). Les largeurs de résonance peuvent aussi être
calculées et dépendent à la fois de  et de
et de  . A l’origine, on retrouve la fréquence linéaire,
i.e.
. A l’origine, on retrouve la fréquence linéaire,
i.e.  .
.
|
|
|
|
L’apparition de résonances de tout ordre sous l’action d’une perturbation, me permet d’introduire un résultat général sur la dynamique d’un système Hamiltonien. En effet, d’après le théorème KAM (cf. page §), nous avons vu que la majorité des trajectoires du système linéaire subsistent sous l’effet d’une faible perturbation15. Par contre, tous les tores résonants sont détruits. La condition de résonance pour deux degrés de liberté est :
 | (2.79) |
Ces orbites sont  -périodiques. Quel est le destin des tores résonants sous l’action d’une
perturbation ? Le théorème des points fixes de Poincaré-Birkhoff (voir par exemple, Arnold et Avez,
1968) stipule que le cercle d’orbites périodiques de fréquence rationnelle
-périodiques. Quel est le destin des tores résonants sous l’action d’une
perturbation ? Le théorème des points fixes de Poincaré-Birkhoff (voir par exemple, Arnold et Avez,
1968) stipule que le cercle d’orbites périodiques de fréquence rationnelle  pour le système
non perturbé dégénère en nombre paire (
pour le système
non perturbé dégénère en nombre paire ( ) points fixes :
) points fixes : 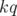 points fixes elliptiques alternés
avec
points fixes elliptiques alternés
avec 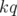 point fixes hyperboliques. Dans chacune des îles, ce schéma peut être appliqué de
nouveau au voisinage des orbites elliptiques (cf. Fig. 2.13).
point fixes hyperboliques. Dans chacune des îles, ce schéma peut être appliqué de
nouveau au voisinage des orbites elliptiques (cf. Fig. 2.13).
|
|
La notion de « dangerosité » d’une résonance pour la dynamique est un problème à part
entière. Par exemple, les résonances 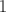 et
et  conduisent toujours à des instabilités
quelque soit l’amplitude d’oscillation initiale
conduisent toujours à des instabilités
quelque soit l’amplitude d’oscillation initiale  : l’ouverture dynamique est nulle ; pour
: l’ouverture dynamique est nulle ; pour
 , la dynamique est toujours stable : l’ouverture dynamique est infinie. Pour toutes
les autres résonances, il existe une amplitude maximale non nulle (
, la dynamique est toujours stable : l’ouverture dynamique est infinie. Pour toutes
les autres résonances, il existe une amplitude maximale non nulle (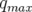 ) au-deçà de
laquelle le mouvement est stable. Au voisinage des points hyperboliques le mouvement est
chaotique mais borné. Par contre aux grandes amplitudes (
) au-deçà de
laquelle le mouvement est stable. Au voisinage des points hyperboliques le mouvement est
chaotique mais borné. Par contre aux grandes amplitudes ( ), les orbites résonantes
sont suffisamment excitées pour détruire toutes les trajectoires. La dernière trajectoire
fermée16
définit l’ouverture dynamique qui est fortement marquée par les résonances (cf. Fig. 2.14 et
Fig. 2.15).
), les orbites résonantes
sont suffisamment excitées pour détruire toutes les trajectoires. La dernière trajectoire
fermée16
définit l’ouverture dynamique qui est fortement marquée par les résonances (cf. Fig. 2.14 et
Fig. 2.15).
Ces résultats me permettent de rappeler, qu’un 2n-pôles peut engendrer des résonances de tout
ordre. En effet, il est parfois affirmé, par exemple, que les hexapôles ne peuvent générer que des
résonances d’ordre un et trois. Cette idée fausse provient du fait que si l’on applique une théorie de
perturbation du premier ordre, seules des résonances d’ordre inférieur à 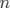 apparaissent (voir par
exemple Hagedorn, 1957, Schoch, 1958 ou Guignard 1978) ; de plus, les calculs ne sont en
général pas faits aux ordres supérieurs (voir par exemple, Bazzani et al., 1994, Bengtsson,
1988).
apparaissent (voir par
exemple Hagedorn, 1957, Schoch, 1958 ou Guignard 1978) ; de plus, les calculs ne sont en
général pas faits aux ordres supérieurs (voir par exemple, Bazzani et al., 1994, Bengtsson,
1988).