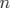 degrés de liberté écrit sous la
forme :
degrés de liberté écrit sous la
forme :
Pour l’écriture de cette partie, je me suis inspiré des articles de J. Laskar décrivant de manière exhaustive la méthode d’Analyse en Fréquence (1992, 1993, 1994 et 1999).
Pour décrire la méthode d’Analyse en Fréquence, nous allons d’abord nous placer dans le
cas général d’un système Hamiltonien autonome à 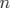 degrés de liberté écrit sous la
forme :
degrés de liberté écrit sous la
forme :
 | (2.61) |
où  représente la partie intégrable du mouvement et
représente la partie intégrable du mouvement et  un terme de perturbation — dans le
cadre de la dynamique d’un accélérateur, nous avons vu au cours du chapitre 1 (page §) que
un terme de perturbation — dans le
cadre de la dynamique d’un accélérateur, nous avons vu au cours du chapitre 1 (page §) que
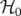 décrit le mouvement bétatron et
décrit le mouvement bétatron et  décrit par exemple les défauts multipolaires
—
décrit par exemple les défauts multipolaires
—
Supposons qu’en l’absence de perturbation ( ), le système puisse s’écrire en variables
actions-angles
), le système puisse s’écrire en variables
actions-angles 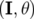 . Alors les équations du mouvement se réduisent à :
. Alors les équations du mouvement se réduisent à :
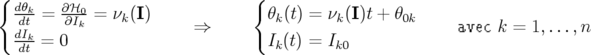 | (2.62) |
Les solutions 2.62 peuvent s’écrire sous forme complexe  , soit :
, soit :
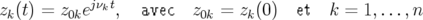 | (2.63) |
Les orbites 2.63 sont confinées sur des tores de dimensions 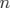 , produits de cercles de rayons
, produits de cercles de rayons
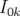 parcourus aux fréquences
parcourus aux fréquences  (cf. Fig. 2.9 pour
(cf. Fig. 2.9 pour  ).
).
|
|
S’il existe une bijection entre les actions et les fréquences, i.e. si la condition de non-dégénérescence suivante est vérifiée :
 | (2.64) |
alors le mouvement peut être décrit de manière équivalente par les actions 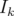 ou les fréquences
ou les fréquences
 ; on définit alors l’application,
; on définit alors l’application,  , dite application fréquence :
, dite application fréquence :
 | (2.65) |
Si de plus, on se place sur une surface d’énergie constante (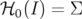 ), alors seulement
), alors seulement
 actions sont indépendantes et l’application fréquence 2.65 devient (si par exemple,
actions sont indépendantes et l’application fréquence 2.65 devient (si par exemple,
 ) :
) :
 | (2.66) |
Le problème qui nous préoccupe est de savoir ce qu’il advient de ces orbites sous l’effet d’une
perturbation faible. La réponse est fournie par le théorème KAM (Kolmogorov-Arnold-Moser, voir
par exemple les références incluses in Laskar, 1999) : sous des conditions très générales, pour une
perturbation suffisamment faible, la plupart des tores du système non perturbé (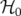 ) subsistent
mais sont déformés. Ce sont les tores dont les vecteurs fréquences vérifient la condition dite
diophantienne :
) subsistent
mais sont déformés. Ce sont les tores dont les vecteurs fréquences vérifient la condition dite
diophantienne :
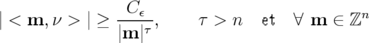 | (2.67) |
où 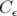 est une constante dépendant de
est une constante dépendant de  et de
et de  : ils sont appelés tores KAM. Les tores de
: ils sont appelés tores KAM. Les tores de  pour lesquels
pour lesquels  sont appelés tores résonants et sont détruits d’après le théorème
KAM. Entre les tores KAM, les orbites sont en général chaotiques. Cependant, il est encore possible
de construire une application fréquence (voir Laskar, 1999). Les solutions KAM peuvent alors
s’exprimer sous la forme :
sont appelés tores résonants et sont détruits d’après le théorème
KAM. Entre les tores KAM, les orbites sont en général chaotiques. Cependant, il est encore possible
de construire une application fréquence (voir Laskar, 1999). Les solutions KAM peuvent alors
s’exprimer sous la forme :
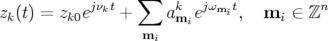 | (2.68) |
Les coefficients 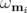 sont combinaison linéaire de
sont combinaison linéaire de 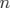 fréquences indépendantes appelées fréquences
fondamentales du système, i.e.
fréquences indépendantes appelées fréquences
fondamentales du système, i.e. 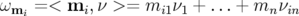 .
.
La méthode d’Analyse en Fréquence repose sur la construction de l’application fréquence
numérique, 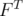 , en recherchant une décomposition quasi-périodique d’une trajectoire sur un temps
d’intégration fini
, en recherchant une décomposition quasi-périodique d’une trajectoire sur un temps
d’intégration fini  et en utilisant une technique de Fourier raffinée (Laskar 1988, 1993 et 1999),
i.e. sous la forme d’un nombre fini
et en utilisant une technique de Fourier raffinée (Laskar 1988, 1993 et 1999),
i.e. sous la forme d’un nombre fini  de termes :
de termes :
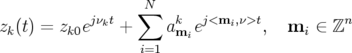 | (2.69) |
où les coefficients  sont ordonnés par amplitude
décroissante14
et
sont ordonnés par amplitude
décroissante14
et  est le vecteur de fréquences fondamentales.
est le vecteur de fréquences fondamentales.
A énergie fixée, une trajectoire de l’espace des phases vit sur une surface d’énergie de
dimension  . Habituellement, on observe le mouvement dans une surface de Poincaré,
i.e. que l’on enregistre une trajectoire discrète en fixant un des angles
. Habituellement, on observe le mouvement dans une surface de Poincaré,
i.e. que l’on enregistre une trajectoire discrète en fixant un des angles 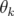 , par exemple
, par exemple
 modulo
modulo 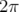 (cf. Fig. 2.10). Les fréquences fondamentales déduites du signal
quasi-périodique 2.69 sont exprimées par rapport à la section de Poincaré, donc par exemple dans
notre cas
(cf. Fig. 2.10). Les fréquences fondamentales déduites du signal
quasi-périodique 2.69 sont exprimées par rapport à la section de Poincaré, donc par exemple dans
notre cas  . Le mouvement est donc restreint sur un espace de dimension
. Le mouvement est donc restreint sur un espace de dimension 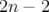 .
.
|
|
Pour l’Analyse en Fréquence, une condition plus stricte est adoptée : on fixe les  angles
angles
 . Dans ce cas, le mouvement est étudié dans un espace de dimension
. Dans ce cas, le mouvement est étudié dans un espace de dimension  . Il est
caractérisé par la donnée de
. Il est
caractérisé par la donnée de  actions.
actions.
En ne conservant que les fréquences fondamentales de la décomposition quasi-périodique
(Eq. 2.69) obtenue après intégration sur un intervalle de temps ![[τ,τ + T ]](these846x.png) , on construit
l’application fréquence numérique :
, on construit
l’application fréquence numérique :
| Fθ0T : ℝ × ℝn−1 | −→ℝn−1 | ||
| (τ,I1,…,In−1) |  (ν1,…,νn−1) (ν1,…,νn−1) | (2.70) |