 va nous donner des informations sur le système
dynamique (résonances, nonlinéarités, chaos).
va nous donner des informations sur le système
dynamique (résonances, nonlinéarités, chaos).
L’étude des propriétés de l’application  va nous donner des informations sur le système
dynamique (résonances, nonlinéarités, chaos).
va nous donner des informations sur le système
dynamique (résonances, nonlinéarités, chaos).
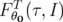 est indépendante du choix dans angles initiaux
est indépendante du choix dans angles initiaux 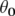 (cf. sur un tore,
les fréquences ne dépendent pas de la phase) et
(cf. sur un tore,
les fréquences ne dépendent pas de la phase) et  est une fonction régulière pour
une trajectoire KAM. Inversement, la non-régularité de
est une fonction régulière pour
une trajectoire KAM. Inversement, la non-régularité de 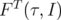 nous permettra de
mettre en évidence les phénomènes résonants et les zones chaotiques.
nous permettra de
mettre en évidence les phénomènes résonants et les zones chaotiques.
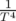 en utilisant une fenêtre
de Hanning alors qu’une transformée de Fourier rapide (FFT) converge en
en utilisant une fenêtre
de Hanning alors qu’une transformée de Fourier rapide (FFT) converge en  (Laskar,
1999). En effet, l’algorithme de la FFT présuppose que le signal recherché est périodique,
alors que l’Analyse en Fréquence cherche à reconstruire une plus grande classe de
signaux, à savoir les signaux quasi-périodiques de la forme (2.69) ; ce point fondamental
rend la méthode plus apte à l’étude d’un système dynamique. Cette propriété permet
de la calculer sur un temps d’intégration
(Laskar,
1999). En effet, l’algorithme de la FFT présuppose que le signal recherché est périodique,
alors que l’Analyse en Fréquence cherche à reconstruire une plus grande classe de
signaux, à savoir les signaux quasi-périodiques de la forme (2.69) ; ce point fondamental
rend la méthode plus apte à l’étude d’un système dynamique. Cette propriété permet
de la calculer sur un temps d’intégration 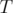 court et de faire de la prédiction à long
terme.
court et de faire de la prédiction à long
terme.
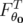 est invariante par translation dans le temps
est invariante par translation dans le temps  pour une trajectoire
régulière (trajectoire KAM). A l’inverse, la variation avec le temps des fréquences,
appelée diffusion, pourra être utilisée comme indice de stabilité et de chaoticité de la
trajectoire.
pour une trajectoire
régulière (trajectoire KAM). A l’inverse, la variation avec le temps des fréquences,
appelée diffusion, pourra être utilisée comme indice de stabilité et de chaoticité de la
trajectoire.
La diffusion des orbites nous donnera de précieuses informations sur la stabilité globale de la dynamique du système étudié. Pour un système à deux degrés de liberté, l’espace des phases est de dimension 4, les surfaces d’énergie de dimension 3 et l’espace des fréquences de dimension 1 (cf. réduction par la conservation de l’énergie). Une orbite KAM est représentée par un point dans l’espace des fréquences et vit sur un tore de dimension 2. Une orbite non régulière n’est pas un point mais une courbe révélant la diffusion entre les orbites régulières (cf. Fig. 2.11-a). Il est clair que dans l’espace des fréquences, un point (dimension 0) sur une courbe de dimension 1 empêche tout mouvement régulier d’avoir de grandes excursions en amplitude. De manière équivalente, en se plaçant dans l’espace des phases, un tore de dimension 2 sépare une surface d’énergie (dimension 3) en une partie intérieure et une partie extérieure : c’est donc une barrière topologique à la diffusion.
Pour un système à trois degrés de liberté, la situation n’est plus du tout la même. Un point n’arrête pas la diffusion dans un plan (cf. Fig. 2.11-b). Vus dans l’espace des phases, les tores de dimension 3 ne sont plus des frontières topologiques à la diffusion pour une surface d’énergie de dimension 5. Cependant il peut être montré que la diffusion est quasi-nulle au voisinage des orbites régulières. Au voisinage d’une trajectoire KAM, la diffusion décroît exponentiellement si bien qu’un grand nombre de trajectoires régulières joue le rôle de barrière effective à la diffusion (résultat de Morbidelli et Gorgilli, 1995).