Introduction
La physique des accélérateurs a connu de profonds bouleversements ces dernières années.
L’augmentation des performances des machines en termes d’énergie, de durée de vie, de taille de
faisceau s’est accompagnée de l’utilisation de champs magnétiques de plus en plus intenses et
complexes (wigglers, onduleurs, solénoïdes, aimants supraconducteurs). Aujourd’hui, le régime de
fonctionnement d’un accélérateur est fortement marqué par des phénomènes nonlinéaires
(résonances, chaos). De nombreux effets aussi bien individuels que collectifs doivent être désormais
compris pour obtenir de hautes performances. Parallèlement, les méthodes d’investigations se sont
développées ; beaucoup proviennent d’ailleurs de la Mécanique Céleste, « berceau » de l’étude
des systèmes dynamiques (méthodes de perturbation, d’intégration, stabilité à long
terme). A cela, il faut ajouter l’essor de l’informatique, un précieux outil du physicien des
accélérateurs.
Le contenu de cette thèse est un exemple de ce lien entre la Physique des Accélérateurs et la
Mécanique Céleste, puisque nous y appliquons une méthode récente, l’Analyse en Fréquence, qui
a été initialement développée pour étudier la dynamique et la stabilité du Système
Solaire sur plusieurs millions d’années (Laskar, 1990). En l’espace d’une seconde, une
particule effectue environ 10 000 révolutions dans le collisionneur électron-positron de 27
km de circonférence du CERN (LEP). L’échelle de temps change mais pas les outils
d’investigation.
Le travail ici-présenté est consacré à l’étude de la dynamique transverse des machines de
rayonnement synchrotron. Il s’articule autour de deux grandes parties. Une première,
théorique, présente les outils utilisés (Hamiltonien, intégrateurs symplectiques, Analyse en
Fréquence) ; des simulations numériques ont été effectuées pour quatre machines : l’ALS
(Berkeley), l’ESRF (Grenoble), SOLEIL (Saclay) et Super-ACO (Orsay). La seconde
partie est dédiée à l’analyse d’expériences réalisées sur deux sources de lumière : l’ALS et
Super-ACO.
Les machines de rayonnement synchrotron de troisième génération sont construites sur des
optiques à forte focalisation afin d’atteindre de performances toujours plus extrêmes : les petites
émittances créées permettent d’obtenir les hautes brillances recherchées. Cependant, de telles
contraintes impliquent l’utilisation de champs magnétiques de forte intensité qui eux-mêmes vont
exciter de nombreuses résonances et risquent ainsi de détériorer la dynamique globale du faisceau et
de conduire à une faible ouverture dynamique et une faible acceptance en énergie. Il en résulte une
injection lente et une faible durée de vie. Ces effets indésirables doivent être minimisés tout en
concervant une haute brillance.
La dynamique des particules individuelles est une des causes principales de la limitation des
performances actuelles des sources de lumière. Si les orbites sont instables aux grandes amplitudes,
alors les électrons diffusés à ces grandes amplitudes lors de collisions avec les atomes du gaz résiduel
(durée de vie liée au vide) ou avec d’autres électrons (durée de vie Touschek) vont être perdus par
le faisceau. Il en sera de même pour les particules injectées à grande amplitude (optimisation de
l’injection).
Une des tâches principales du physicien des accélérateurs consiste d’abord à déterminer la
meilleure optique possible de la machine, ensuite à définir une modélisation aussi proche que
possible de la réalité et enfin, à développer des méthodes susceptibles d’améliorer la stabilité de la
dynamique du faisceau.
La première étape consiste à modéliser chacun des éléments magnétiques d’un anneau de
stockage. L’approche que nous avons retenue (chapitre 1) est une approche hamiltonienne
locale : chaque élément magnétique (dipôle, quadripôle, multipôle) est modélisé par
un Hamiltonien local à trois degrés de liberté, exprimé en coordonnées rectilignes ou
curvilignes suivant la géométrie de l’élément. Dans chacun des cas, les approximations choisies
sont explicitées. Le champ magnétique est toujours exprimé en considérant un profil
magnétique longitudinal rectangulaire. Suivant le type d’élément et le rayon de l’accélérateur,
les approximations des petits angles et des grandes machines seront ou non prises en
compte.
La formulation hamiltonienne est particulièrement adaptée pour étudier la dynamique
nonlinéaire et pour construire un intégrateur numérique des équations du mouvement. Bien que de
nombreux codes dits de tracking existent déjà actuellement (e.g. les codes BETA, DESPOT, MAD
et TRACY), ils ne sont pas optimisés et ne permettent pas de modéliser la dynamique à long terme
aussi bien des petites et des grandes machines. Les spécificités recherchées sont d’obtenir un
code numérique dédié exclusivement au tracking. Il doit pouvoir permettre d’intégrer
en un temps optimum la trajectoire d’une particule (chargée) sur plusieurs millions de
tours, et ceci pour de très nombreuses conditions initiales, de contrôler la précision et les
approximations réalisées. Le but consiste à caractériser de manière quasi-exhaustive
la dynamique du faisceau circulant dans un accélérateur. Pour toutes ces raisons, les
approches matricielles, les approches fondées sur le calcul de l’application de premier
retour de l’accélérateur ou permettant de calculer des formes normales n’ont pas été
retenues.
La méthode d’intégration numérique que nous présentons est symplectique et repose
sur l’utilisation de l’algèbre de Lie (chapitre 2). Ces nouvelles méthodes sont déjà très
répandues aux Etats-Unis, elles ont plus de mal à s’établir en Europe. L’intégrateur le
plus utilisé aujourd’hui pour les machines à électrons repose sur le travail de Forest
et Ruth (1990) : c’est un intégrateur d’ordre 4. Nous présentons une nouvelle classe
d’intégrateurs à pas d’intégration tous positifs (Laskar et Robutel, 2000). Ce sont des
intégrateurs particulièrement adaptés à des Hamiltoniens 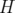 décomposables en deux parties
décomposables en deux parties
 et
et 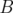 complètement intégrables où
complètement intégrables où 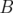 joue le rôle d’un terme de perturbation :
joue le rôle d’un terme de perturbation :
 . Il est possible de construire des intégrateurs d’ordre
. Il est possible de construire des intégrateurs d’ordre  de reste
de reste  où
où  est le pas d’intégration. Il est souvent possible d’adjoindre un correcteur pour
que le reste devienne un
est le pas d’intégration. Il est souvent possible d’adjoindre un correcteur pour
que le reste devienne un 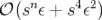 . L’intégrateur que nous avons retenu est plus
précis que celui de Forest et Ruth d’un ordre de grandeur pour un nombre constant
d’évaluations.
. L’intégrateur que nous avons retenu est plus
précis que celui de Forest et Ruth d’un ordre de grandeur pour un nombre constant
d’évaluations.
Les équations du mouvement intégrées, la dynamique des différentes machines de
rayonnement synchrotron est étudiée au moyen de l’Analyse en Fréquence. C’est un
outil extrêmement puissant reposant sur une technique de Fourier raffinée et permettant
d’obtenir la décomposition complète d’un signal quasi-périodique. Nous commençons par
l’appliquer à deux systèmes dynamiques simples : le pendule et l’application d’Hénon. Le
pendule permet de décrire la dynamique au voisinage d’une résonance. L’application
d’Hénon permet de modéliser les perturbations introduites par un hexapôle dans une
maille.
L’Analyse en Fréquence est une méthode particulièrement adaptée à la description de
la dynamique d’un système à trois degrés de liberté comme celle d’un accélérateur et
permet de manière assez intuitive et pratique d’identifier des résonances et d’estimer leur
amplitude. Cette méthode est appliquée à la description théorique de quatre sources de
lumière (chapitre 3) : l’ALS, l’ESRF, le projet SOLEIL et Super-ACO. Pour chacune de ces
machines, nous calculons une carte en fréquence ainsi que l’ouverture dynamique associée
pour différentes configurations (chromaticités, points de fonctionnement, énergie de la
particule, défauts du champ magnétique). Une carte en fréquence décrit la variation des
nombres d’ondes avec les amplitudes d’oscillation horizontale et verticale. Nous montrons la
grande sensibilité de la dynamique aux réglages magnétiques et définissons un indice de
stabilité corrélé à la variation temporelle des nombres d’ondes (diffusion des orbites).
L’ensemble des résultats ne prend en compte que la dynamique transverse en négligeant le
mouvement longitudinal. Les cartes en fréquence mettent en évidence clairement les principales
résonances, en particulier les résonances couplées non vues ni étudiées dans les processus
traditionnels d’optimisation de l’optique d’une machine. L’utilisation de la diffusion des orbites
permet également d’identifier les résonances dans l’espace des configurations (l’ouverture
dynamique).
Dans un anneau de stockage, la périodicité interne permet d’améliorer la dynamique du faisceau
en limitant le nombre de résonances pouvant être excitées ; cependant la présence de défauts
quadripolaires est une des causes principales de brisure de cette symétrie et entraîne souvent une
détérioration de la durée de vie et du taux d’injection via l’excitation de nonlinéarités. Une
connaissance précise des défauts magnétiques est donc nécessaire pour établir un modèle aussi
réaliste que possible de la machine ; ce travail est délicat, si bien que souvent l’écart entre les
performances escomptées et réelles pour une machine donnée peut atteindre plus d’un
facteur deux. L’analyse en fréquence est ici utilisée pour réaliser ce lien entre théorie et
expérience.
A ces fins, des expériences innovantes ont été menées à l’ALS et Super-ACO (deuxième
partie). Pour obtenir une modélisation aussi réaliste que possible de l’ALS, les matrices
réponses expérimentales sont analysées pour déduire les défauts de gradients droits et
tournés. Ce travail essentiel (Robin, Safranek et Decking, 1999) a été obtenu en utilisant le
programme LOCO (Safranek, 1997). L’étape suivante consistait à pouvoir comparer la
dynamique simulée et réelle de l’accélérateur. Nous présentons au chapitre 4 la première
carte en fréquence expérimentale d’un accélérateur (Robin, Steier, Laskar, Nadolski :
2000, « Global Dynamics of the Advanced Light Source Revealed through Experimental
Frequency Map Analysis »). Sa réalisation a été possible grâce à l’utilisation conjointe de
moniteurs de position tour par tour et de deux aimants rapides permettant de simuler
les amplitudes initiales d’oscillations bétatrons horizontales et verticales. Les cartes en
fréquences mesurées et simulées sont en excellent accord. Les expériences ont été réalisées
pour le point de fonctionnement nominal de l’anneau de stockage mais aussi pour des
réglages magnétiques proches de nœuds de résonances. La diffusion des orbites y a été
mesurée. Ces résultats permettent d’envisager l’utilisation de l’Analyse en Fréquence en
tant qu’outil en ligne (diagnostic de la dynamique du faisceau) dans la salle de contrôle
d’un accélérateur. L’Analyse en Fréquence peut aussi être utilisée indépendamment de
tout modèle pour valider une modélisation. Ce point est fondamental puisqu’il permet
ensuite de faire des simulations fiables de l’impact de la modification de la structure de
l’anneau.
Le dépouillement et l’analyse de l’ensemble des données expérimentales a nécessité de
comprendre des effets connexes liés au fait que nous ne mesurons pas le signal d’une particule
individuelle mais d’un faisceau d’environ 40 milliards d’électrons. Nous présentons une modélisation
de la décohérence à une et deux dimensions.
Des expériences faites à Super-ACO (chapitre 5) nous ont permis d’améliorer notre
compréhension de la dynamique linéaire et nonlinéaire. La première étape a nécessité d’adapter le
programme LOCO pour déterminer le premier jeu de gradients mesurés de l’anneau.
Trois matrices réponses ont été acquises et analysées pour trois configurations distinctes :
hexapôles éteints, hexapôles allumés, hexapôles allumés et onduleurs fermés. Les défauts
déduits sont compatibles avec les tolérances magnétiques. Pour comprendre les écarts
importants de performances entre la théorie et la simulation, nous avons réalisé les premières
mesures, à Super-ACO, du glissement des nombres d’ondes avec l’amplitude horizontale
pour les trois configurations précédentes. Super-ACO ne disposant pas de moniteur de
position tour par tour, nous avons utilisé le signal collecté sur une simple électrode.
Utilisant l’Analyse en Fréquence, le principal résultat est la mise en évidence d’un fort
pseudo-octupôle (non modélisé jusqu’à présent) issu des champs de fuite des quadripôles. Les
implications sont importantes et permettent de mieux comprendre les performances actuelles de
l’anneau.
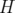 décomposables en deux parties
décomposables en deux parties
 et
et 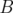 complètement intégrables où
complètement intégrables où 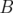 joue le rôle d’un terme de perturbation :
joue le rôle d’un terme de perturbation :
 . Il est possible de construire des intégrateurs d’ordre
. Il est possible de construire des intégrateurs d’ordre  de reste
de reste  où
où  est le pas d’intégration. Il est souvent possible d’adjoindre un correcteur pour
que le reste devienne un
est le pas d’intégration. Il est souvent possible d’adjoindre un correcteur pour
que le reste devienne un 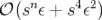 . L’intégrateur que nous avons retenu est plus
précis que celui de Forest et Ruth d’un ordre de grandeur pour un nombre constant
d’évaluations.
. L’intégrateur que nous avons retenu est plus
précis que celui de Forest et Ruth d’un ordre de grandeur pour un nombre constant
d’évaluations.