B.3 L’ESRF : point de fonctionnement nominal
Les deux réglages magnétiques nominaux de l’ESRF ont été étudiés. L’anneau est supposé
idéale avec sa 16-périodicité. Le point de fonctionnement est dans les deux cas le même :
 avec des chromaticités légèrement surcompensées :
avec des chromaticités légèrement surcompensées :  et
et
 . Les deux réglages diffèrent uniquement par la pente à l’origine de la courbe en
fréquence
. Les deux réglages diffèrent uniquement par la pente à l’origine de la courbe en
fréquence 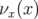 qui est modifiée en ajustement les forces des hexapôles. Expérimentalement le
second réglage semble meilleur à fort courant par paquet en termes de durée de vie (communication
personnelle, A. Ropert).
qui est modifiée en ajustement les forces des hexapôles. Expérimentalement le
second réglage semble meilleur à fort courant par paquet en termes de durée de vie (communication
personnelle, A. Ropert).
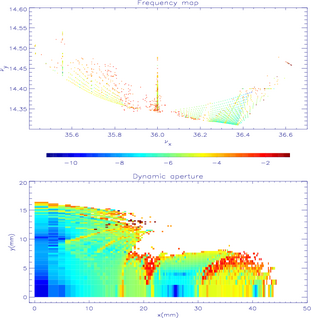
Pour le premier réglage hexapolaire (cf. Fig. B.10), les ouvertures dynamiques et cartes en
fréquence ont été tracées pour les deux quadrants (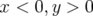 ) et (
) et ( ). L’ouverture
dynamique est très grande si l’on ne prend pas en compte les résonances dans l’estimation de ses
dimensions.
). L’ouverture
dynamique est très grande si l’on ne prend pas en compte les résonances dans l’estimation de ses
dimensions.
La dynamique est dominée à faible amplitude par la résonance d’ordre 5, 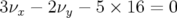 atteinte pour
atteinte pour  mm dans l’espace des configurations (et
mm dans l’espace des configurations (et 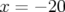 mm). Elle est traversée
suivant une région elliptique pour (
mm). Elle est traversée
suivant une région elliptique pour (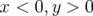 ) : dans l’espace des fréquences, on la voit
nettement ; les particules sont capturées dans les îlots de résonance ; sa largeur est grande (cf.
désertion de points de chaque coté de la résonance sur la carte en fréquence Fig. B.10 de gauche).
Sur l’ouverture dynamique, on observe nettement les régions hyperboliques (jaune-orange)
entourant la région elliptique (vert) pour
) : dans l’espace des fréquences, on la voit
nettement ; les particules sont capturées dans les îlots de résonance ; sa largeur est grande (cf.
désertion de points de chaque coté de la résonance sur la carte en fréquence Fig. B.10 de gauche).
Sur l’ouverture dynamique, on observe nettement les régions hyperboliques (jaune-orange)
entourant la région elliptique (vert) pour  mm. Dans le quadrant (
mm. Dans le quadrant (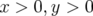 ), cette
résonance est traversée suivant la région hyperbolique pour
), cette
résonance est traversée suivant la région hyperbolique pour 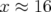 mm, la diffusion est plus
élevée (cf. Fig. B.11).
mm, la diffusion est plus
élevée (cf. Fig. B.11).
A plus grande amplitude, la dynamique est dominée par la résonance entière  . Sa largeur
est grande : toutes les particules peuplant l’ouverture dynamique pour
. Sa largeur
est grande : toutes les particules peuplant l’ouverture dynamique pour  mm sont
capturées par la résonance. Bien que la majorité de ces conditions initiales correspondent au régime
elliptique (vert sur l’ouverture dynamique), la résonance entière apparaît avec une grande
diffusion sur la carte en fréquence (orange). Cet artefact provient simplement de la manière
dont la carte en fréquence est tracée : les faibles amplitudes puis les grandes amplitudes
(orange).
mm sont
capturées par la résonance. Bien que la majorité de ces conditions initiales correspondent au régime
elliptique (vert sur l’ouverture dynamique), la résonance entière apparaît avec une grande
diffusion sur la carte en fréquence (orange). Cet artefact provient simplement de la manière
dont la carte en fréquence est tracée : les faibles amplitudes puis les grandes amplitudes
(orange).
Pour la machine réelle, cette résonance ne pourra pas être traversée sans réduction importante
des performances : en pratique toutes les particules pour 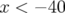 mm (Fig. B.10) et
mm (Fig. B.10) et 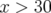 mm
(Fig. B.11), i.e. à gauche de la résonance entière seront instables. Une estimation raisonable des
dimensions de l’ouverture dynamique serait :
mm
(Fig. B.11), i.e. à gauche de la résonance entière seront instables. Une estimation raisonable des
dimensions de l’ouverture dynamique serait : ![[− 27, 21 ]y=0 × [− 7, 7]x=0](these2708x.png) mm et même :
mm et même :
![[−20,16]y=0 × [− 7, 7]x=0](these2709x.png) mm si la résonance d’ordre 5 n’était pas traversée.
mm si la résonance d’ordre 5 n’était pas traversée.
Pour le second jeu hexapolaire, l’allure de carte en fréquence est complètement modifiée (cf.
Fig. B.10). La diffusion globale est plus faible puisque la résonance entière n’est plus atteinte. La
carte en fréquence a une petite extension dans l’espace des fréquences, peu de résonances sont
rencontrées. La principale résonance 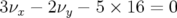 atteinte à grande amplitude :
atteinte à grande amplitude :
 mm (région elliptique sur Fig. B.11 de gauche) et
mm (région elliptique sur Fig. B.11 de gauche) et 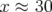 mm (région
hyperbolique sur Fig. B.11 de droite).
mm (région
hyperbolique sur Fig. B.11 de droite).
 avec des chromaticités légèrement surcompensées :
avec des chromaticités légèrement surcompensées :  et
et
 . Les deux réglages diffèrent uniquement par la pente à l’origine de la courbe en
fréquence
. Les deux réglages diffèrent uniquement par la pente à l’origine de la courbe en
fréquence 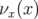 qui est modifiée en ajustement les forces des hexapôles. Expérimentalement le
second réglage semble meilleur à fort courant par paquet en termes de durée de vie (communication
personnelle, A. Ropert).
qui est modifiée en ajustement les forces des hexapôles. Expérimentalement le
second réglage semble meilleur à fort courant par paquet en termes de durée de vie (communication
personnelle, A. Ropert).
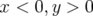 ) et (
) et ( ). L’ouverture
dynamique est très grande si l’on ne prend pas en compte les résonances dans l’estimation de ses
dimensions.
). L’ouverture
dynamique est très grande si l’on ne prend pas en compte les résonances dans l’estimation de ses
dimensions.
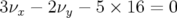 atteinte pour
atteinte pour  mm dans l’espace des configurations (et
mm dans l’espace des configurations (et 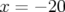 mm). Elle est traversée
suivant une région elliptique pour (
mm). Elle est traversée
suivant une région elliptique pour (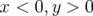 )
) mm. Dans le quadrant (
mm. Dans le quadrant (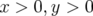 ), cette
résonance est traversée suivant la région hyperbolique pour
), cette
résonance est traversée suivant la région hyperbolique pour 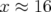 mm, la diffusion est plus
élevée (cf. Fig.
mm, la diffusion est plus
élevée (cf. Fig.  . Sa largeur
est grande
. Sa largeur
est grande mm sont
capturées par la résonance. Bien que la majorité de ces conditions initiales correspondent au régime
elliptique (vert sur l’ouverture dynamique), la résonance entière apparaît avec une grande
diffusion sur la carte en fréquence (orange). Cet
mm sont
capturées par la résonance. Bien que la majorité de ces conditions initiales correspondent au régime
elliptique (vert sur l’ouverture dynamique), la résonance entière apparaît avec une grande
diffusion sur la carte en fréquence (orange). Cet 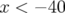 mm (Fig.
mm (Fig. 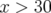 mm
(Fig.
mm
(Fig. ![[− 27, 21 ]y=0 × [− 7, 7]x=0](these2708x.png) mm et même
mm et même![[−20,16]y=0 × [− 7, 7]x=0](these2709x.png) mm si la résonance d’ordre 5 n’était pas traversée.
mm si la résonance d’ordre 5 n’était pas traversée.
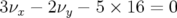 atteinte à grande amplitude
atteinte à grande amplitude mm (région elliptique sur Fig.
mm (région elliptique sur Fig. 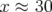 mm (région
hyperbolique sur Fig.
mm (région
hyperbolique sur Fig. 
 (
(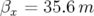 et
et 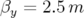 ). La
dynamique est dominée par la résonance de couplage 3
). La
dynamique est dominée par la résonance de couplage 3 .
Les zones elliptiques et hyperboliques associées sont nettement identifiables sur l’ouverture
dynamique.
.
Les zones elliptiques et hyperboliques associées sont nettement identifiables sur l’ouverture
dynamique. 
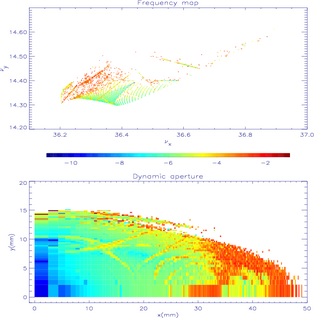
 (
(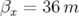 et
et 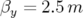 ).
La dynamique est dominée par la résonance
).
La dynamique est dominée par la résonance 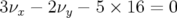 atteinte à grande
amplitude.
atteinte à grande
amplitude.