5.1.1 Description du programme LOCO
Dans un anneau de stockage, la périodicité interne permet d’améliorer la dynamique du faisceau en
limitant le nombre de résonances pouvant être excitées ; cependant la présence de défauts
quadripolaires
est une des causes principales de brisure de cette symétrie et entraîne souvent une détérioration de
la durée de vie et du taux d’injection via l’excitation de nonlinéarités. Donc, lorsque l’on désire
optimiser une machine, une connaissance précise des défauts magnétiques est nécessaire pour
établir un modèle aussi réaliste que possible ; alors seulement, les calculs d’ouverture dynamique, de
carte en fréquence prennent tout leur sens.
Le programme LOCO (Linear Optics from Closed Orbits) a été écrit par Safranek (1997) dans cette
optique pour analyser la matrice-réponse du National Synchrotron Light Source de Brookhaven et en
déduire les gradients des quadripôles, les défauts des éléments magnétiques (alignements, rotations des
éléments). Tout le programme repose sur l’analyse de l’orbite fermée en approximation linéaire. Cette
méthode
a déjà eu de nombreuses applications — voir par exemple pour l’Advanced Light Source (Robin et
al., 1996) et pour l’anneau VUV du National Synchrotron Source (Safranek et Kramer, 1997)
—
Dans ce travail, on se propose d’appliquer LOCO à Super-ACO. Dans une première partie, la
méthode de calcul de la matrice-réponse est rappelée. Puis l’utilisation du programme LOCO est
présentée et testée sur un exemple simple. Enfin, l’expérience du 19 juin 2000 est dépouillée : trois
matrices-réponse ont été acquises pour trois configurations distinctes : hexapôles éteints, hexapôles
allumés, hexapôles allumés et onduleurs fermés.
Le principal objectif est d’établir le jeu de défauts des gradients pour chaque cas et de valider la
méthode. En discussion, une application des résultats est proposée pour restaurer la symétrie de
Super-ACO.
5.1.1.1 Perturbation de l’orbite fermée par un kick dipolaire
Soit un dipôle fin de longueur  , situé en
, situé en  , donnant un angle ou impulsion (kick en
anglais)
, donnant un angle ou impulsion (kick en
anglais)  à une particule, avec
à une particule, avec  la rigidité magnétique et
la rigidité magnétique et 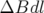 le champ
dipolaire intégré. Si juste avant l’impulsion, l’orbite fermée est
le champ
dipolaire intégré. Si juste avant l’impulsion, l’orbite fermée est  , alors juste après
l’impulsion, elle devient
, alors juste après
l’impulsion, elle devient  . Trouver l’expression de l’orbite fermée
. Trouver l’expression de l’orbite fermée 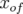 en
en 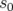 revient à
résoudre la relation de fermeture :
revient à
résoudre la relation de fermeture :
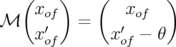 | (5.1) |
où 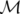 est la matrice de transfert de l’anneau sur un tour. La solution, exprimée en fonction des
paramètres de Twiss
est la matrice de transfert de l’anneau sur un tour. La solution, exprimée en fonction des
paramètres de Twiss 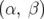 , du nombre d’ondes
, du nombre d’ondes  , est alors :
, est alors :
Pour déduire l’expression de l’orbite fermée résultante en un endroit  quelconque de
l’anneau, il suffit de propager la solution trouvée en
quelconque de
l’anneau, il suffit de propager la solution trouvée en  en utilisant la fonction de Green,
en utilisant la fonction de Green,
 , de l’équation de Hill :
, de l’équation de Hill :
5.1.1.2 Matrice-réponse
Pour un jeu de défauts dipolaires  , en utilisant la linéarité de l’équation de Hill en la
perturbation dipolaire, l’orbite fermée résultante est simplement la superposition des orbites
fermées individuelles créées par une impulsion
, en utilisant la linéarité de l’équation de Hill en la
perturbation dipolaire, l’orbite fermée résultante est simplement la superposition des orbites
fermées individuelles créées par une impulsion  (cf. Eq. 5.2), soit :
(cf. Eq. 5.2), soit :
La matrice 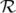 est appelée matrice-réponse linéaire de l’orbite fermée. Elle est constituée de
est appelée matrice-réponse linéaire de l’orbite fermée. Elle est constituée de 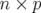 éléments pour une machine comportant
éléments pour une machine comportant  correcteurs dipolaires et
correcteurs dipolaires et 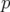 BPM (Beam Position
Monitors : stations de mesure de position).
BPM (Beam Position
Monitors : stations de mesure de position).
En expérience et en simulation avec le programme
MAD
[50], la matrice-réponse est construite en allumant l’un après l’autre les 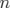 correcteurs et en
enregistrant dans chacun des
correcteurs et en
enregistrant dans chacun des 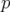 BPM l’orbite fermée générée.
BPM l’orbite fermée générée.
Expérimentalement, deux matrices sont construites : une pour des kicks d’angle  et une
autre pour des kicks d’angle
et une
autre pour des kicks d’angle  . En effet, il subsiste une orbite fermée résiduelle créée par les
nonlinéarités des champs magnétiques. En calculant la différence de ces deux matrices, on élimine
ainsi l’orbite fermée résiduelle et l’on obtient une matrice-réponse équivalente à un kick d’angle
. En effet, il subsiste une orbite fermée résiduelle créée par les
nonlinéarités des champs magnétiques. En calculant la différence de ces deux matrices, on élimine
ainsi l’orbite fermée résiduelle et l’on obtient une matrice-réponse équivalente à un kick d’angle
 .
.
Le choix de la valeur du kick dipolaire est guidé par les deux considérations suivantes : d’une
part, une grande valeur de 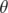 permet d’augmenter le rapport signal sur bruit de la mesure et donc
de réduire la barre d’erreur sur les valeurs de gradients trouvées par rapport au bruit aléatoire des
BPM ; d’autre part, une faible valeur de
permet d’augmenter le rapport signal sur bruit de la mesure et donc
de réduire la barre d’erreur sur les valeurs de gradients trouvées par rapport au bruit aléatoire des
BPM ; d’autre part, une faible valeur de  permet de s’affranchir des nonlinéarités mais aussi de
rester dans une gamme de réponse linéaire de l’électronique. Une valeur intermédiaire doit donc
être choisie : en pratique des kicks de valeur induisant une perturbation de l’orbite fermée de
permet de s’affranchir des nonlinéarités mais aussi de
rester dans une gamme de réponse linéaire de l’électronique. Une valeur intermédiaire doit donc
être choisie : en pratique des kicks de valeur induisant une perturbation de l’orbite fermée de  mm rms (valeur optimale pour le NSLS X-Ray Ring à Brookhaven :
mm rms (valeur optimale pour le NSLS X-Ray Ring à Brookhaven : 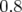 mm rms — Safranek, 1997
—).
mm rms — Safranek, 1997
—).
Le programme LOCO utilise une méthode des moindres carrés pour minimiser le «  » entre
la matrice-réponse modèle,
» entre
la matrice-réponse modèle,  , et la matrice-réponse expérimentale,
, et la matrice-réponse expérimentale, 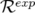 , en ajustant les
gradients quadripolaires :
, en ajustant les
gradients quadripolaires :
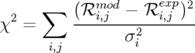 | (5.4) |
où la sommation a lieu sur les BPM  et les correcteurs
et les correcteurs 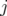 , normalisée par le bruit des BPM
, normalisée par le bruit des BPM  et
en utilisant une méthode de décomposition en valeurs singulières (SVD [96]). Les autres
paramètres pouvant être incorporés dans l’ajustement de la matrice-réponse non couplée sont
les gains des correcteurs (
et
en utilisant une méthode de décomposition en valeurs singulières (SVD [96]). Les autres
paramètres pouvant être incorporés dans l’ajustement de la matrice-réponse non couplée sont
les gains des correcteurs (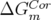 ), les gains des BPM (
), les gains des BPM ( ) et le glissement de
l’énergie (
) et le glissement de
l’énergie (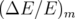 ). Pour la matrice couplée, il faut ajouter la rotation des BPM et des
correcteurs.
). Pour la matrice couplée, il faut ajouter la rotation des BPM et des
correcteurs.
Minimiser le 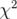 revient à minimiser la norme du vecteur
revient à minimiser la norme du vecteur  dont les composantes sont définies
par :
dont les composantes sont définies
par :
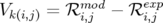 | (5.5) |
où l’indice 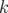 varie de
varie de  à
à 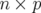 . Alors en approximation linéaire, on
obtient :
. Alors en approximation linéaire, on
obtient :
La valeur escomptée du  est le nombre de degrés de liberté, soit
est le nombre de degrés de liberté, soit  avec un écart
type
avec un écart
type  avec
avec 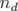 le nombre de données (taille du vecteur
le nombre de données (taille du vecteur  ) et
) et  le
nombre de paramètres ajustés (cf. Modeling of Data, chap. 15 in Numerical Recipes,
1992).
le
nombre de paramètres ajustés (cf. Modeling of Data, chap. 15 in Numerical Recipes,
1992).
 , situé en
, situé en  , donnant un angle ou impulsion (kick en
anglais)
, donnant un angle ou impulsion (kick en
anglais)  à une particule, avec
à une particule, avec  la rigidité magnétique et
la rigidité magnétique et 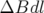 le champ
dipolaire intégré. Si juste avant l’impulsion, l’orbite fermée est
le champ
dipolaire intégré. Si juste avant l’impulsion, l’orbite fermée est  , alors juste après
l’impulsion, elle devient
, alors juste après
l’impulsion, elle devient  . Trouver l’expression de l’orbite fermée
. Trouver l’expression de l’orbite fermée 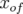 en
en 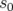 revient à
résoudre la relation de fermeture :
revient à
résoudre la relation de fermeture :
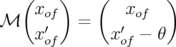
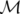 est la matrice de transfert de l’anneau sur un tour. La solution, exprimée en fonction des
paramètres de Twiss
est la matrice de transfert de l’anneau sur un tour. La solution, exprimée en fonction des
paramètres de Twiss 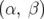 , du nombre d’ondes
, du nombre d’ondes  , est alors
, est alors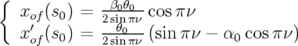
 quelconque de
l’anneau, il suffit de propager la solution trouvée en
quelconque de
l’anneau, il suffit de propager la solution trouvée en  en utilisant la fonction de Green,
en utilisant la fonction de Green,
 , de l’équation de Hill
, de l’équation de Hill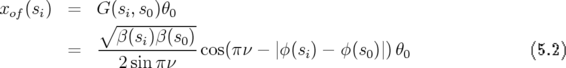
 , en utilisant la linéarité de l’équation de Hill en la
perturbation dipolaire, l’orbite fermée résultante est simplement la superposition des orbites
fermées individuelles créées par une impulsion
, en utilisant la linéarité de l’équation de Hill en la
perturbation dipolaire, l’orbite fermée résultante est simplement la superposition des orbites
fermées individuelles créées par une impulsion  (cf. Eq.
(cf. Eq. 
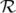 est appelée
est appelée 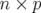 éléments pour une machine comportant
éléments pour une machine comportant  correcteurs dipolaires et
correcteurs dipolaires et 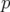 BPM (
BPM (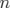 correcteurs et en
enregistrant dans chacun des
correcteurs et en
enregistrant dans chacun des 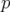 BPM l’orbite fermée générée.
BPM l’orbite fermée générée.
 et une
autre pour des
et une
autre pour des  . En effet, il subsiste une orbite fermée résiduelle créée par les
nonlinéarités des champs magnétiques. En calculant la différence de ces deux matrices, on élimine
ainsi l’orbite fermée résiduelle et l’on obtient une matrice-réponse équivalente à un
. En effet, il subsiste une orbite fermée résiduelle créée par les
nonlinéarités des champs magnétiques. En calculant la différence de ces deux matrices, on élimine
ainsi l’orbite fermée résiduelle et l’on obtient une matrice-réponse équivalente à un  .
.
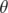 permet d’augmenter le rapport signal sur bruit de la mesure et donc
de réduire la barre d’erreur sur les valeurs de gradients trouvées par rapport au bruit aléatoire des
BPM
permet d’augmenter le rapport signal sur bruit de la mesure et donc
de réduire la barre d’erreur sur les valeurs de gradients trouvées par rapport au bruit aléatoire des
BPM permet de s’affranchir des nonlinéarités mais aussi de
rester dans une gamme de réponse linéaire de l’électronique. Une valeur intermédiaire doit donc
être choisie
permet de s’affranchir des nonlinéarités mais aussi de
rester dans une gamme de réponse linéaire de l’électronique. Une valeur intermédiaire doit donc
être choisie mm rms (valeur optimale pour le NSLS X-Ray Ring à Brookhaven
mm rms (valeur optimale pour le NSLS X-Ray Ring à Brookhaven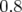 mm rms — Safranek, 1997
—).
mm rms — Safranek, 1997
—).
 » entre
la matrice-réponse modèle,
» entre
la matrice-réponse modèle,  , et la matrice-réponse expérimentale,
, et la matrice-réponse expérimentale, 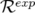 , en ajustant les
gradients quadripolaires
, en ajustant les
gradients quadripolaires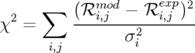
 et les correcteurs
et les correcteurs 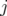 , normalisée par le bruit des BPM
, normalisée par le bruit des BPM  et
en utilisant une méthode de décomposition en valeurs singulières (SVD
et
en utilisant une méthode de décomposition en valeurs singulières (SVD 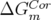 ), les gains des BPM (
), les gains des BPM ( ) et le glissement de
l’énergie (
) et le glissement de
l’énergie (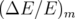 ). Pour la matrice couplée, il faut ajouter la rotation des BPM et des
correcteurs.
). Pour la matrice couplée, il faut ajouter la rotation des BPM et des
correcteurs.
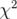 revient à minimiser la norme du vecteur
revient à minimiser la norme du vecteur  dont les composantes sont définies
par
dont les composantes sont définies
par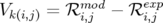
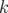 varie de
varie de  à
à 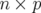 . Alors en approximation linéaire, on
obtient
. Alors en approximation linéaire, on
obtient
 est le nombre de degrés de liberté, soit
est le nombre de degrés de liberté, soit  avec un écart
type
avec un écart
type  avec
avec 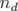 le nombre de données (taille du vecteur
le nombre de données (taille du vecteur  ) et
) et  le
nombre de paramètres ajustés (cf.
le
nombre de paramètres ajustés (cf.