5.1.7 Matrice-réponse hexapôles allumés et onduleurs fermés
5.1.7.1 Conditions expérimentales
La matrice-réponse avec les onduleurs fermés a été acquise pour un courant  mA dans 24
paquets — dimensions faisceau
mA dans 24
paquets — dimensions faisceau  —. Les courants quadripolaires et
hexapolaires mesurés sont donnés par le tableau 5.11 ; les gradients des familles Q3 et Q4 ont été
modifiés pour compenser globalement la focalisation induite par les insertions.
—. Les courants quadripolaires et
hexapolaires mesurés sont donnés par le tableau 5.11 ; les gradients des familles Q3 et Q4 ont été
modifiés pour compenser globalement la focalisation induite par les insertions.
|
|
|
| | Famille | I(A) | Famille | I(A) |
|
|
|
| | Q1 | 218.50 | H1 | 54.35 |
| Q2 | 399.31 | H2 | 100.31 |
| Q3 | 377.88 | H3 | 198.58 |
| Q4 | 212.16 | H4 | 193.93 |
|
|
|
| | |
| TAB. 5.11: | Courants mesurés dans les
familles de quadripôles — hexapôles et
onduleurs fermés — Les courant des
familles Q1 et Q2 ont changé de manière
significative. Valeurs utilisées pour calibrer
le modèle de Super-ACO. |
|
|
Dans la version 8.15 de MAD, les onduleurs ne sont pas modélisables. L’ensemble des résultats
obtenus avec LOCO ne sera à prendre en compte que de manière qualitative. Cependant
l’ajustement ayant lieu principalement sur les fonctions optiques, les nombres d’ondes trouvés
seront très proches des valeurs expérimentales. Par contre, les variations sur les gradients
n’ont pas de signification physique, car ils ne tiennent pas compte de la focalisation des
onduleurs.
Si l’on considère une maille de Super-ACO avec les gradients quadripolaires et champs
hexapolaires mesurés via les courants mais sans onduleur, le point de fonctionnement vaut
 , qu’il faut ensuite modifier pour ajouter l’influence de la focalisation des
onduleurs.
, qu’il faut ensuite modifier pour ajouter l’influence de la focalisation des
onduleurs.
Les glissements des nombres d’ondes induits par l’ensemble des onduleurs (cf. Fig. 5.28) SU2,
SU3, SU6, SU7 et SU8 sont  . Ces valeurs calculées en utilisant
les valeurs expérimentales de courant (cf. Tab. 5.11) sont très proches des mesures réalisées au
début des années 1990 — Brunelle, 1992 — (cf. Tab. 5.12), le point de fonctionnement devient
après l’ajustement
. Ces valeurs calculées en utilisant
les valeurs expérimentales de courant (cf. Tab. 5.11) sont très proches des mesures réalisées au
début des années 1990 — Brunelle, 1992 — (cf. Tab. 5.12), le point de fonctionnement devient
après l’ajustement 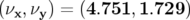 auquel il faudrait encore ajouter l’influence de l’orbite
fermée non nulle dans les hexapôles.
auquel il faudrait encore ajouter l’influence de l’orbite
fermée non nulle dans les hexapôles.
|
|
|
|
|
| | | SU2 | SU3 | SU6 | SU7 | SU8 |
|
|
|
|
|
| 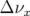 | 0.0053 | -0.007 | 0.0007 | 0.00 | -0.0016 |
 | 0.0477 | 0.046 | 0.0030 | 0.03 | 0.0275 |
|
|
|
|
|
| | |
| TAB. 5.12: | Glissement des nombres d’ondes expérimentaux induit par chacun des onduleurs.
Les onduleurs SU2, SU3, SU7 et SU8 vont le plus perturber l’optique de Super-ACO. |
|
Dans le code BETA [93], les onduleurs sont modélisés
idéalement,
i.e. sans focalisation horizontale ( et
et  ). Le point de fonctionnement déduit des
valeurs expérimentales de courant est alors
). Le point de fonctionnement déduit des
valeurs expérimentales de courant est alors 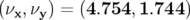 .
.
5.1.7.2 Dispersion mesurée dans les BPM
Les dispersions mesurées dans les BPM sont exprimées dans le tableau 5.13. Ne disposant pas de
modèle satisfaisant de l’anneau avec les onduleurs, on ne donnera pas de comparaison avec un
hypothétique modèle mais avec les valeurs mesurées de la fonction dispersion dans les deux cas
précédents (Fig. 5.29 et Fig. 5.30). La comparaison n’est donnée qu’à titre qualitatif puisque les
familles Q3 et Q4, réglant les dispersions, sont différentes. La grande différence concerne
la dispersion est maintenant positive dans les régions à faible dispersion (BPM 1, 4,
16) : en moyenne, les écarts relatifs sont de près de 150 % pour ces trois BPM. Par
contre dans les régions dispersives, les écarts relatifs restent faibles : inférieurs à  en
moyenne.
en
moyenne.
|
|
|
| | BPM1 | 52 | BPM09 | -92 |
| BPM2 | 1199 | BPM10 | 1331 |
| BPM3 | 1215 | BPM11 | 1279 |
| BPM4 | 24 | BPM12 | -76 |
| BPM5 | -44 | BPM13 | -12 |
| BPM6 | 1235 | BPM14 | 1235 |
| BPM7 | 1287 | BPM15 | 1179 |
| BPM8 | -72 | BPM16 | 20 |
|
|
|
| | |
| TAB. 5.13: | Dispersion horizontale mesurée (à  mm) dans les BPM de Super-ACO —
hexapôles allumés, onduleurs fermés — La fonction dispersion dans les régions non dispersives
a beaucoup changé. Dans les BPM 1, 4 et 16, la fonction dispersion est maintenant positive. mm) dans les BPM de Super-ACO —
hexapôles allumés, onduleurs fermés — La fonction dispersion dans les régions non dispersives
a beaucoup changé. Dans les BPM 1, 4 et 16, la fonction dispersion est maintenant positive. |
|
-
Régions non dispersives
- l’écart modèle-mesure est en moyenne de 45%.
-
Régions dispersives
- l’écart modèle-mesure est en moyenne de 5%.
5.1.7.3 Résultats obtenus avec LOCO
Tous les résultats suivants doivent être considérés qualitativement. L’algorithme LOCO converge
bien dans les deux plans avec des écarts 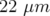 (H) et
(H) et  (V) et un point de fonctionnement
de
(V) et un point de fonctionnement
de  . L’allure des fonctions
. L’allure des fonctions 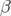 (Fig. 5.32) est déformée en particulier au
voisinage des onduleurs. Qualitativement, elle est en accord avec celle prédite par le code BETA.
Retenons simplement, que LOCO donne une bonne estimation de l’allure des fonctions optiques et
des nombres d’ondes. La perturbation de l’optique linéaire par les onduleurs SU2, SU3, SU7 et SU8
est nettement observée.
(Fig. 5.32) est déformée en particulier au
voisinage des onduleurs. Qualitativement, elle est en accord avec celle prédite par le code BETA.
Retenons simplement, que LOCO donne une bonne estimation de l’allure des fonctions optiques et
des nombres d’ondes. La perturbation de l’optique linéaire par les onduleurs SU2, SU3, SU7 et SU8
est nettement observée.
A titre indicatif, les variations sur les gradients sont données par la figure 5.31 : les écarts sont
de plusieurs pour cent. Comme les onduleurs ne sont pas inclus dans la description de la maille
utilisée par le code LOCO, ces valeurs ne doivent pas être considérées comme réalistes. Par contre,
il est intéressant de comprendre comment le programme LOCO a ajusté l’optique linéaire de
l’anneau de stockage.
Nous avons vu que les onduleurs induisent des glissements importants des nombres d’ondes en
particulier dans le plan vertical (cf. Tab. 5.12) ; les onduleurs SU2, SU3, SU7 et SU8 perturbent
fortement l’optique de Super-ACO. Le code LOCO compense localement la perturbation de chaque
onduleur en modifiant les gradients des quadripôles adjacents dont la focalisation est verticale. C’est
pourquoi, des variations relatives de plusieurs pour cent sont observées. En pratique,
l’influence des onduleurs est compensée globalement sauf pour SU8 (Brunelle et al.,
1999).
 mA dans 24
paquets — dimensions faisceau
mA dans 24
paquets — dimensions faisceau  —. Les courants quadripolaires et
hexapolaires mesurés sont donnés par le tableau 5.11 ; les gradients des familles Q3 et Q4 ont été
modifiés pour compenser globalement la focalisation induite par les insertions.
—. Les courants quadripolaires et
hexapolaires mesurés sont donnés par le tableau 5.11 ; les gradients des familles Q3 et Q4 ont été
modifiés pour compenser globalement la focalisation induite par les insertions.

 , qu’il faut ensuite modifier pour ajouter l’influence de la focalisation des
onduleurs.
, qu’il faut ensuite modifier pour ajouter l’influence de la focalisation des
onduleurs.
 . Ces valeurs calculées en utilisant
les valeurs expérimentales de courant (cf. Tab.
. Ces valeurs calculées en utilisant
les valeurs expérimentales de courant (cf. Tab. 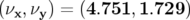 auquel il faudrait encore ajouter l’influence de l’orbite
fermée non nulle dans les hexapôles.
auquel il faudrait encore ajouter l’influence de l’orbite
fermée non nulle dans les hexapôles.
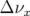

 et
et  ). Le point de fonctionnement déduit des
valeurs expérimentales de courant est alors
). Le point de fonctionnement déduit des
valeurs expérimentales de courant est alors 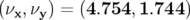 .
.
 en
moyenne.
en
moyenne.
 mm) dans les BPM de Super-ACO —
hexapôles allumés, onduleurs fermés — La fonction dispersion dans les régions non dispersives
a beaucoup changé. Dans les BPM 1, 4 et 16, la fonction dispersion est maintenant positive.
mm) dans les BPM de Super-ACO —
hexapôles allumés, onduleurs fermés — La fonction dispersion dans les régions non dispersives
a beaucoup changé. Dans les BPM 1, 4 et 16, la fonction dispersion est maintenant positive.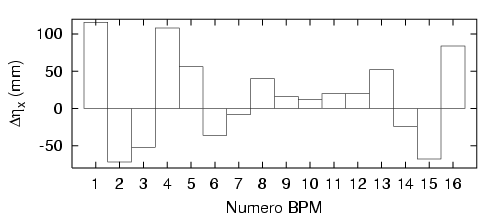

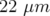 (H) et
(H) et  (V) et un point de fonctionnement
de
(V) et un point de fonctionnement
de  . L’allure des fonctions
. L’allure des fonctions 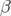 (Fig.
(Fig. 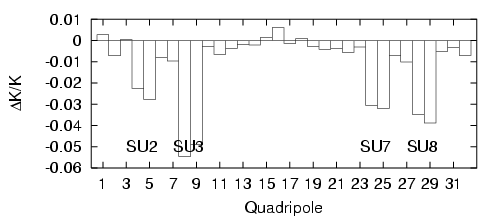

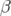 calculées pour une machine théorique avec le logiciel BETA (ligne)
et déduites l’ajustement avec les hexapôles et les onduleurs fermés (étoile). On observe un
bon accord qualitatif avec le modèle (cf. Brunelle, 1992).
calculées pour une machine théorique avec le logiciel BETA (ligne)
et déduites l’ajustement avec les hexapôles et les onduleurs fermés (étoile). On observe un
bon accord qualitatif avec le modèle (cf. Brunelle, 1992).