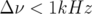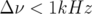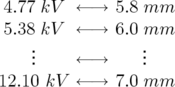5.3.2 Point de routine avec minimum de couplage

5.3.2.1 Conditions expérimentales

• On travaille avec le point de routine (cf. paramètres expérimentaux Tab. 5.20) en faisant le minimum de couplage (réglage : ).
• Un total de 13 mesures a été réalisé à la fois pour le BPM4 et pour le BPM12.
• La tension du perturbateur P4 varie entre 4.77 kV et 12.10 kV, le courant de 18.4 mA à 16.7 mA.
• La décohérence est faible : plusieurs milliers de tours (cf. Fig. 5.66).

  4.7296 H1 (A) 54.34 1.7000 H2 (A) 100.30 1.9 H3 (A) 201.42 1.9 H4 (A) 204.68 QT4 (A) 0.56 QT6 (A) -0.54 TAB. 5.20: Caractéristiques machine : point de fonctionnement de routine avec minimum de couplage. Valeurs utilisées pour ajuster le modèle de Super-ACO.

    

  FIG. 5.66: Signal collecté (u.a.) sur le bouton HE en fonction du nombre de tours pour un kick de 10.87 kV : la décohérence est faible.

5.3.2.2 Espace des phases

• De manière similaire aux expériences du 22 mai 2000, l’étalonnage des BPM avec des bumps statiques ne peut pas être utilisé pour déduire une calibration entre la tension du perturbateur P4 et l’amplitude donnée au faisceau. En effet, en utilisant cette calibration, on déduirait la correspondance :

  (5.44)

• Pour cette étude, l’étalonnage doit être fait en fonction du signal sur le perturbateur et non de celui lu sur le bouton HE. L’explication peut provenir du fait que n’utilisant qu’une seule électrode, le signal collecté est un mélange entre les coordonnées transverses (x-y).
• Par comparaison des courbes des variations théoriques des nombres d’ondes avec l’amplitude (cf. infra), on utilisera la calibration :

  (5.45)

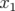• Pour les différentes tensions du perturbateur, on peut tracer le signal lu sur le premier BPM () en fonction de celui lu sur le deuxième (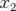). Un exemple de pseudo-ellipse est représenté sur la figure 5.67. L’épaississement est une conséquence directe de la décohérence du faisceau qui, dans ce cas, est lente (plusieurs milliers de tours).
• Une tentative de reconstruction du vrai espace des phases avec (cf. Eq. 5.42) est illustrée par la figure 5.68.
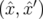• En utilisation les coordonnées de Courant-Snyder , l’ellipse d’émittance se transforme en cercle :

  (5.46)

  FIG. 5.67: Trajectoire dans le pseudo-espace des phases (). L’épaississement de l’ellipse est une conséquence de la faible décohérence du faisceau (sur 1 000 tours, cf. Fig. 5.66).

   

  FIG. 5.68: Trajectoire dans l’espace des phases () : la pente de l’ellipse est directement reliée au fonctions de Twiss par le facteur . L’amplitude est donnée dans le coin supérieur gauche des figures.

  En utilisant ces coordonnées normalisées, l’espace des phases pour les différents kicks est tracé (cf. Fig. 5.69 et Fig. 5.70).

  • On remarque que la courbe épaissie obtenue n’est pas parfaitement un cercle. Les raisons sont d’une part que les fonctions de Twiss sont théoriques et non mesurées et d’autre part que le signal analysé est un mélange des deux coordonnées transverses.
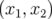  • On note que l’espace est très déformé pour  kV et surtout pour  kV. Aucun phénomène particulier (résonance, perturbations externes) n’a pu être mis explicitement en évidence.
  • Aux grandes amplitudes les ellipses épaissies se déforment, caractérisant la présence de nonlinéarités.

FIG. 5.70: Espace des phases normalisé pour de grandes amplitudes : les ellipses sont déformées par les nonlinéarités. L’amplitude est donnée dans le coin supérieur gauche des figures.

5.3.2.3 Courbe en fréquence

• En utilisant l’algorithme d’Analyse en Fréquence, l’extraction des nombres d’ondes avec une grande précision est possible.
• Seul le nombre d’ondes peut être extrait du signal puisque le minimum de couplage est réalisé.
• Le nombre d’ondes mesuré suit une loi quadratique croissante de l’amplitude contrairement à un modèle²⁶ sans composante de type octupolaire forte (cf. Fig. 5.71).
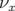• La bonne loi de comportement est retrouvée en introduisant les pseudo-octupôles induits par les champs de fuite des quadripôles. En utilisant les données du tableau 5.20 et la formule de glissement du nombre d’ondes (Eq. 5.35), la contribution des pseudo-octupôles au nombre d’ondes horizontal s’écrit :

  (5.47)

avec , la fonction au niveau du moniteur de position.

FIG. 5.71: Courbe en fréquence en fonction de l’amplitude horizontale. Comparaison entre la mesure (carrés) et différentes modélisations de Super-ACO : sans composante octupolaire (cercles) et avec pseudo-octupôles (croix). L’écart subsistant peut être expliqué par l’incertitude sur les fonctions .