 :
:
Dans cette annexe, nous présentons les cartes en fréquence et ouvertures dynamiques des quatre machines étudiées : SOLEIL (section B.1), Super-ACO (section B.2), l’ESRF (section B.3) et l’ALS (section B.4). Ce sont les mêmes figures que celles en noir et blanc déjà présentées dans le corps de ce mémoire. La diffusion est ici codée suivant une échelle logarithmique de couleur allant du bleu pour une diffusion quasi nulle au rouge pour une diffusion élevée.
Nous rappelons l’expression de l’indice de diffusion utilisé, noté  :
:
 |
où  et
et  sont les nombres d’ondes calculés sur les
sont les nombres d’ondes calculés sur les  premiers tours de machine et
premiers tours de machine et  et
et
 ceux calculés pour les
ceux calculés pour les  tours suivants.
tours suivants.
Le codage de la diffusion en couleur va faciliter la localisation des résonances dans l’ouverture dynamique : en particulier les régions hyperboliques où la diffusion est élevée vont être mises en exergue.
Nous présentons les cartes en fréquence et ouvertures dynamiques pour l’optique faible émittance
numéro 1 (Fig. B.1) et l’optique faible émittance numéro 1 modifiée (Fig. B.2). Le point de
fonctionnement est  , les chromaticités naturelles sont parfaitement
compensées.
, les chromaticités naturelles sont parfaitement
compensées.
Pour le premier cas, la dynamique est marquée par la résonance d’ordre 7,  ,
qui est atteinte pour
,
qui est atteinte pour  mm (cf. Fig. B.1). A faible amplitude, la diffusion est faible (vert), le
mouvement est quasipériodique et régulier. A grande amplitude, la dynamique est perturbée par le
nœud avec la résonance
mm (cf. Fig. B.1). A faible amplitude, la diffusion est faible (vert), le
mouvement est quasipériodique et régulier. A grande amplitude, la dynamique est perturbée par le
nœud avec la résonance  : les largeurs de résonances se superposent, le mouvement
est chaotique avec une diffusion élevée (orange-rouge).
: les largeurs de résonances se superposent, le mouvement
est chaotique avec une diffusion élevée (orange-rouge).
Le second cas a été optimisé de manière à éviter les résonances précédentes. A ces fins, les forces des hexapôles ont été modifiées : l’objectif est atteint (cf. Fig. B.2). La carte en fréquence est en contrepartie repliée sur elle-même, les dimensions de l’ouverture dynamiques sont similaires au réglage précédent avec une diffusion plus faible.
|
La carte en fréquence de Super-ACO modélisée comme machine idéale est donnée par la figure B.3.
Toute la partie pour 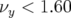 n’est pas représentée : elle correspond aux particules qui ont des
nombres d’ondes au-delà de la résonance principale
n’est pas représentée : elle correspond aux particules qui ont des
nombres d’ondes au-delà de la résonance principale  et aux amplitudes
et aux amplitudes
 mm dans l’ouverture dynamique. Suivant que l’on trace la carte en fréquence pour le
premier (
mm dans l’ouverture dynamique. Suivant que l’on trace la carte en fréquence pour le
premier (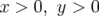 ) et second (
) et second (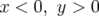 ) quadrant, la résonance principale est
traversée soit selon une région hyperbolique (peu de points en son voisinage cf. Fig. B.3 de
gauche), soit selon une région elliptique (cf. Fig. B.3 de droite). Dans ce cas, comme la
résonance a une grande largeur, un grand nombre de particules est capturé dans les îles
de résonance : sur la carte en fréquence, on observe nettement la droite de résonance ;
l’ouverture dynamique est « gonflée » (cf. région
) quadrant, la résonance principale est
traversée soit selon une région hyperbolique (peu de points en son voisinage cf. Fig. B.3 de
gauche), soit selon une région elliptique (cf. Fig. B.3 de droite). Dans ce cas, comme la
résonance a une grande largeur, un grand nombre de particules est capturé dans les îles
de résonance : sur la carte en fréquence, on observe nettement la droite de résonance ;
l’ouverture dynamique est « gonflée » (cf. région  mm et
mm et  de l’ouverture
dynamique).
de l’ouverture
dynamique).
|
|
En incluant dans la modélisation de Super-ACO, les défauts de gradients quadripolaires issus des mesures magnétiques, la dynamique de l’anneau est peu modifiée (cf. Fig. B.4). Globalement, la diffusion est plus élevée, de nouvelles résonances sont excitées ; la symétrie 4 de l’anneau est brisée mais les défauts sont faibles : de l’ordre du pour mille (comparer avec la carte Fig. B.3 de gauche).
Pour le point de fonctionnement nominal, le point de fonctionnement est déplacé de
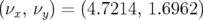 à
à  et surtout les chromaticités ne sont plus
nulles mais surcompensées aux valeurs
et surtout les chromaticités ne sont plus
nulles mais surcompensées aux valeurs  et
et 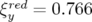 . Les forces des quatre familles
hexapolaires sont donc complètement modifiées, si bien que la dynamique est complètement
différente (cf. Fig. B.5). Le glissement des nombres d’ondes avec l’amplitude est faible : la carte en
fréquence est très « compacte » dans l’espace des fréquences, l’ouverture dynamique est réduite de
près d’un facteur deux dans le plan horizontal ; elle est limitée par la résonance d’ordre 3,
. Les forces des quatre familles
hexapolaires sont donc complètement modifiées, si bien que la dynamique est complètement
différente (cf. Fig. B.5). Le glissement des nombres d’ondes avec l’amplitude est faible : la carte en
fréquence est très « compacte » dans l’espace des fréquences, l’ouverture dynamique est réduite de
près d’un facteur deux dans le plan horizontal ; elle est limitée par la résonance d’ordre 3,
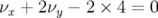 . Expérimentalement, cette résonance est observée mais à plus basse
amplitude.
. Expérimentalement, cette résonance est observée mais à plus basse
amplitude.
|
|
Les mesures expérimentales du glissement des nombres d’ondes avec l’amplitude ont permis de
mettre en évidence l’influence des champs de fuites des quadripôles de Super-ACO. Cet effet peut
être modélisé par un pseudo-octupôle : pour la présente étude, nous avons modifié le modèle de
Super-ACO en incluant un octupôle équivalent au milieu de chacun des quadripôles de l’anneau. La
dynamique du faisceau est complètement modifiée (comparer les figures B.6 et B.7) : le sens de
variation de 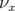 avec l’amplitude est inversé, la carte en fréquence ne présente plus de repliement et
a avec une grande extension spatiale. Le nombre de résonances est plus élevé mais les largeurs des
résonances restent faibles si bien que l’ouverture dynamique est plus grande que sans composante
octupolaire.
avec l’amplitude est inversé, la carte en fréquence ne présente plus de repliement et
a avec une grande extension spatiale. Le nombre de résonances est plus élevé mais les largeurs des
résonances restent faibles si bien que l’ouverture dynamique est plus grande que sans composante
octupolaire.
Lors des mesures expérimentales, il a été possible d’éteindre les familles hexapolaires H1 et H2
tout en conservant le faisceau dans l’anneau. La figure B.8 présente la dynamique associée qui est
fortement altérée : la carte en fréquence est modifiée, en particulier le sens de variation de  (cf. bord droit de la carte B.8 et Fig. B.7) ; de nombreuses résonances sont excitées et
principalement la résonance
(cf. bord droit de la carte B.8 et Fig. B.7) ; de nombreuses résonances sont excitées et
principalement la résonance 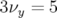 ; l’ouverture dynamique verticale est réduite de près d’un
facteur deux (influence de
; l’ouverture dynamique verticale est réduite de près d’un
facteur deux (influence de 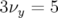 ). L’ouverture dynamique horizontale est trois fois plus
petite.
). L’ouverture dynamique horizontale est trois fois plus
petite.
Enfin pour simuler la dynamique réelle de l’anneau, nous avons volontairement surestimé
l’effet des champs de fuite. Les largeurs de résonances sont alors plus importantes et
peuvent se recouvrir surtout à grande amplitude conduisant à des mouvements chaotiques
(comparer les figures B.9 et B.7). La diffusion est élevée ; l’ouverture dynamique est
constellée de résonances. Une analyse plus détaillée suggère comme nouvelles dimensions :
![[−15,0]× [0, 6]](these2690x.png) mm, en prenant en compte les résonances. Ces dimensions seraient alors proches
de l’expérience.
mm, en prenant en compte les résonances. Ces dimensions seraient alors proches
de l’expérience.
|
|
|
|
Les deux réglages magnétiques nominaux de l’ESRF ont été étudiés. L’anneau est supposé
idéale avec sa 16-périodicité. Le point de fonctionnement est dans les deux cas le même :
 avec des chromaticités légèrement surcompensées :
avec des chromaticités légèrement surcompensées :  et
et
 . Les deux réglages diffèrent uniquement par la pente à l’origine de la courbe en
fréquence
. Les deux réglages diffèrent uniquement par la pente à l’origine de la courbe en
fréquence 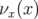 qui est modifiée en ajustement les forces des hexapôles. Expérimentalement le
second réglage semble meilleur à fort courant par paquet en termes de durée de vie (communication
personnelle, A. Ropert).
qui est modifiée en ajustement les forces des hexapôles. Expérimentalement le
second réglage semble meilleur à fort courant par paquet en termes de durée de vie (communication
personnelle, A. Ropert).
Pour le premier réglage hexapolaire (cf. Fig. B.10), les ouvertures dynamiques et cartes en
fréquence ont été tracées pour les deux quadrants (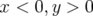 ) et (
) et ( ). L’ouverture
dynamique est très grande si l’on ne prend pas en compte les résonances dans l’estimation de ses
dimensions.
). L’ouverture
dynamique est très grande si l’on ne prend pas en compte les résonances dans l’estimation de ses
dimensions.
La dynamique est dominée à faible amplitude par la résonance d’ordre 5, 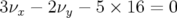 atteinte pour
atteinte pour  mm dans l’espace des configurations (et
mm dans l’espace des configurations (et 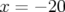 mm). Elle est traversée
suivant une région elliptique pour (
mm). Elle est traversée
suivant une région elliptique pour (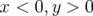 ) : dans l’espace des fréquences, on la voit
nettement ; les particules sont capturées dans les îlots de résonance ; sa largeur est grande (cf.
désertion de points de chaque coté de la résonance sur la carte en fréquence Fig. B.10 de gauche).
Sur l’ouverture dynamique, on observe nettement les régions hyperboliques (jaune-orange)
entourant la région elliptique (vert) pour
) : dans l’espace des fréquences, on la voit
nettement ; les particules sont capturées dans les îlots de résonance ; sa largeur est grande (cf.
désertion de points de chaque coté de la résonance sur la carte en fréquence Fig. B.10 de gauche).
Sur l’ouverture dynamique, on observe nettement les régions hyperboliques (jaune-orange)
entourant la région elliptique (vert) pour  mm. Dans le quadrant (
mm. Dans le quadrant (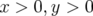 ), cette
résonance est traversée suivant la région hyperbolique pour
), cette
résonance est traversée suivant la région hyperbolique pour 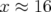 mm, la diffusion est plus
élevée (cf. Fig. B.11).
mm, la diffusion est plus
élevée (cf. Fig. B.11).
A plus grande amplitude, la dynamique est dominée par la résonance entière  . Sa largeur
est grande : toutes les particules peuplant l’ouverture dynamique pour
. Sa largeur
est grande : toutes les particules peuplant l’ouverture dynamique pour  mm sont
capturées par la résonance. Bien que la majorité de ces conditions initiales correspondent au régime
elliptique (vert sur l’ouverture dynamique), la résonance entière apparaît avec une grande
diffusion sur la carte en fréquence (orange). Cet artefact provient simplement de la manière
dont la carte en fréquence est tracée : les faibles amplitudes puis les grandes amplitudes
(orange).
mm sont
capturées par la résonance. Bien que la majorité de ces conditions initiales correspondent au régime
elliptique (vert sur l’ouverture dynamique), la résonance entière apparaît avec une grande
diffusion sur la carte en fréquence (orange). Cet artefact provient simplement de la manière
dont la carte en fréquence est tracée : les faibles amplitudes puis les grandes amplitudes
(orange).
Pour la machine réelle, cette résonance ne pourra pas être traversée sans réduction importante
des performances : en pratique toutes les particules pour 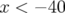 mm (Fig. B.10) et
mm (Fig. B.10) et 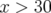 mm
(Fig. B.11), i.e. à gauche de la résonance entière seront instables. Une estimation raisonable des
dimensions de l’ouverture dynamique serait :
mm
(Fig. B.11), i.e. à gauche de la résonance entière seront instables. Une estimation raisonable des
dimensions de l’ouverture dynamique serait : ![[− 27, 21 ]y=0 × [− 7, 7]x=0](these2708x.png) mm et même :
mm et même :
![[−20,16]y=0 × [− 7, 7]x=0](these2709x.png) mm si la résonance d’ordre 5 n’était pas traversée.
mm si la résonance d’ordre 5 n’était pas traversée.
Pour le second jeu hexapolaire, l’allure de carte en fréquence est complètement modifiée (cf.
Fig. B.10). La diffusion globale est plus faible puisque la résonance entière n’est plus atteinte. La
carte en fréquence a une petite extension dans l’espace des fréquences, peu de résonances sont
rencontrées. La principale résonance 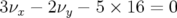 atteinte à grande amplitude :
atteinte à grande amplitude :
 mm (région elliptique sur Fig. B.11 de gauche) et
mm (région elliptique sur Fig. B.11 de gauche) et 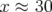 mm (région
hyperbolique sur Fig. B.11 de droite).
mm (région
hyperbolique sur Fig. B.11 de droite).
|
|
|
|
L’Advanced Light Source a été étudiée comme machine parfaite avec sa 12-périodicité.
Dans ce cas, l’ouverture dynamique est très grande ![[0, 22 ] × [0, 10]](these2725x.png) mm (cf. Fig. B.12).
De nombreuses résonances sont excitées dont l’identification est facilitée en utilisant la
diffusion des orbites (jaune-orange). A grandes amplitudes, les largeurs de résonance se
recouvrent conduisant à un mouvement nonlinéaire voire chaotique avec une diffusion élevée
(rouge). La dynamique est dominée à grande amplitude par la résonance de couplage
mm (cf. Fig. B.12).
De nombreuses résonances sont excitées dont l’identification est facilitée en utilisant la
diffusion des orbites (jaune-orange). A grandes amplitudes, les largeurs de résonance se
recouvrent conduisant à un mouvement nonlinéaire voire chaotique avec une diffusion élevée
(rouge). La dynamique est dominée à grande amplitude par la résonance de couplage
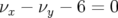 .
.
|
|
Pour obtenir un modèle de l’ALS plus proche des observations expérimentales, nous avons introduit les défauts des quadripôles droits déduits des matrices réponses expérimentales (cf. Fig. B.13), puis ceux des quadripôles tournés pour obtenir un couplage effectif de 1% (cf. Fig. B.14). La 12-périodicité de l’anneau est alors brisée, les largeurs de résonances sont plus grandes. L’ouverture dynamique horizontale (12 mm cf. Fig. B.14) est très proche de celle mesurée en expérience.
Enfin, nous avons obtenu la première carte en fréquence expérimentale d’un accélérateur (cf.
Fig. B.15). Elle correspondrait au voisinage du point de fonctionnement de la carte B.14 où la
diffusion est faible (vert). Pour cette expérience, le point de fonctionnement a volontairement été
déplacé à 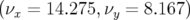 . La carte en fréquence expérimentale révèle un réseau
de résonances d’ordre 5,
. La carte en fréquence expérimentale révèle un réseau
de résonances d’ordre 5,  ,
, 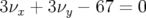 ,
,  et
et
 . Au nœud de résonances, la diffusion des particules est élevée (la durée de vie
et l’efficacité d’injection sont fortement réduites). L’accord entre l’expérience et la modélisation de
l’ALS est remarquable.
. Au nœud de résonances, la diffusion des particules est élevée (la durée de vie
et l’efficacité d’injection sont fortement réduites). L’accord entre l’expérience et la modélisation de
l’ALS est remarquable.
|
|
|
|