 peut être intégrée sans aucune approximation en coordonnées
rectangulaires ou curvilignes. Ces résultats permettront de pouvoir de vérifier la validité des
approximations réalisées, i.e. le développement Taylor usuel de la racine carrée.
peut être intégrée sans aucune approximation en coordonnées
rectangulaires ou curvilignes. Ces résultats permettront de pouvoir de vérifier la validité des
approximations réalisées, i.e. le développement Taylor usuel de la racine carrée.
Dans cette annexe, nous présentons des calculs et résultats complémentaires au chapitre 2 sur les intégrateurs symplectiques. Les applications de transfert des éléments principaux d’un accélérateur sont présentées pour d’autres approximations. Les équations du mouvement de la section droite sont nonlinéaires du fait du caractère relativiste des particules ; elles peuvent être intégrées sans aucune approximation en coordonnées rectangulaires (section A.1) ou curvilignes (section A.3). Les équations du mouvemnt pour un élément dipolaire sont intégrées en conservant la racine carrée du terme cinématique en coordonnées curvilignes (section A.2.1) ou rectangulaires (section A.2.2), l’expression de l’application de transfert des coins dipolaires en est ensuite déduite (section A.2.3). L’application de transfert du dipôle est présentée (section A.2.4), celle du dipôle simple avec le terme des petites machines (section A.2.6). Enfin, nous présentons la modélisation symplectique du déplacement ou de la rotation d’un élément magnétique (section A.3). Ces résultats sont pour la plupart issus des travaux de A.J. Dragt et E. Forest.
La section droite de longueur  peut être intégrée sans aucune approximation en coordonnées
rectangulaires ou curvilignes. Ces résultats permettront de pouvoir de vérifier la validité des
approximations réalisées, i.e. le développement Taylor usuel de la racine carrée.
peut être intégrée sans aucune approximation en coordonnées
rectangulaires ou curvilignes. Ces résultats permettront de pouvoir de vérifier la validité des
approximations réalisées, i.e. le développement Taylor usuel de la racine carrée.
Hamiltonien : Son expression est rappelée en coordonnées rectangulaires (cf. Eq. 1.35 p. § avec
 et
et  ) :
) :
 | (A.1) |
avec pour équations du mouvement :
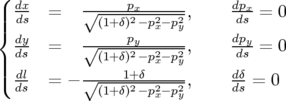 | (A.2) |
Intégration des équations : Les variables  sont encore cycliques, et l’on
obtient :
sont encore cycliques, et l’on
obtient :
 | (A.3) |
avec  la longueur de la section droite.
la longueur de la section droite.
J’ai annoncé page §, que le dipôle est complètement intégrable. Le but de section est de le
montrer. Les équations sont toujours exprimées en fonctions des variables canoniques
 .
.
Description et Hamiltonien : Pour la présente annexe, le dipôle est décrit en introduisant le
cœfficient  qui dans la majorité des cas est égal à la courbure
qui dans la majorité des cas est égal à la courbure  (Forest et al., 1994). Cette
expression est néanmoins utile pour déduire l’expression d’une rotation en géométrie curviligne (cf.
infra). Le Hamiltonien retenu est celui établi page § avec le potentiel vecteur donné par la
formule 1.51 :
(Forest et al., 1994). Cette
expression est néanmoins utile pour déduire l’expression d’une rotation en géométrie curviligne (cf.
infra). Le Hamiltonien retenu est celui établi page § avec le potentiel vecteur donné par la
formule 1.51 :
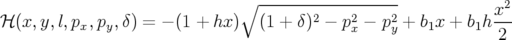 | (A.4) |
Les équations du mouvement deviennent :
 | = px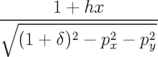 | (A.5a) |
 | = py | (A.5b) |
 | = −(1 + δ)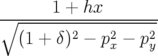 | (A.5c) |
 | = h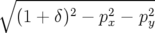 − b1(1 + hx) − b1(1 + hx) | (A.5d) |
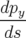 | = 0 | (A.5e) |
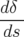 | = 0 | (A.5f) |
Hypothèse de calcul : La seule hypothèse est l’approximation hard-edge. Le Hamiltonien A.4 est complètement intégrable.
Intégration exacte : Les variables  et
et 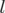 sont cycliques, donc leurs moments conjugués
respectifs sont constants :
sont cycliques, donc leurs moments conjugués
respectifs sont constants :
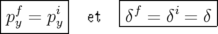 | (A.6) |
L’intégration des autres variables se fait par étapes successives. On commence par l’équation
différentielle de  en utilisant les expressions (Eq. A.5d) puis (Eq. A.5b) :
en utilisant les expressions (Eq. A.5d) puis (Eq. A.5b) :
| dpx | = h ds − b1(1 + hx)ds ds − b1(1 + hx)ds | ||
= 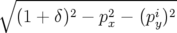 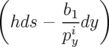 | |||
| yf | = yi +  ∫ ∫
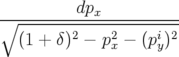 + +  ∫
hds ∫
hds | ||
yf = yi +   + + 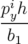 s s | (A.7) |
 |
On déduit alors la solution pour 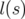 en comparant les équations A.5b et A.5c :
en comparant les équations A.5b et A.5c :
lf = li + 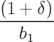  + +  s s | (A.8) | ||
| L’équation différentielle A.5d pour px(s) s’intégre en se servant des expressions A.5a et A.5c : | |||
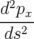 = = | − hpx  − b1h − b1h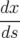 | ||
| = | − h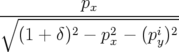 ![[ ∘ -------2----2----i-2 ]
h (1 + δ) + p x − (py) − b1(1 + hx )](these2506x.png) | ||
+ b1hpx | |||
| soit après simplification : | |||
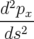 | = −h2p x2 ⇒ p x = a cos(hs) + b sin(hs) | ||
| où les constantes a et b sont déterminées en fonction des conditions initiales, soit : | |||
pxf = p
xi cos(hs) + 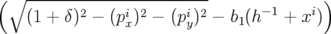 sin(hs) sin(hs) | (A.9) | ||
| L’intégration de la dernière équation (x(s)) est alors immédiate : | |||
 | = h − b1(h−1 + xf) − b1(h−1 + xf) | ||
xf =   | (A.10) | ||
Hamiltonien et description : Il est également possible d’exprimer l’application de transfert en
géométrie cartésienne. Le Hamiltonien est alors le même que celui en géométrie curviligne (cf.
Eq. A.4) avec  :
:
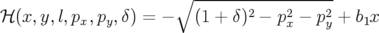 | (A.11) |
Hypothèse de calcul : La seule hypothèse est l’approximation hard-edge. Le Hamiltonien A.11 est complètement intégrable.
Intégration des équations : L’expression des solutions s’obtient à partie des celles de l’aimant
secteur (Eq. A.6 à A.10) en prenant la limite  (Forest, 1994) :
(Forest, 1994) :
![(| (∘ ------------f---------- ∘ ----------------------)
||| xf = xi + 1b1- (1 + δ)2 − (px)2 − (piy)2 − (1 + δ)2 − (pix)2 − (piy)2
|||
|||| pfx = pix − b1s[ ]
||{ f i piy- -----pix----- -----pfx------
y = y + b1 arcsin√ (1+δ)2−-(piy)2 − arcsin √ (1+δ)2−-(piy)2
|| f i
||| py = py [ ]
||| f i (1+δ) -----pix----- -----pfx------
|||| l = l + b1 arcsin√ (1+δ)2−(piy)2 − arcsin √(1+δ)2− (piy)2
|( f
δ = δ](these2517x.png) | (A.12) |
avec  et généralement
et généralement  .
.
Description : Les applications de transfert du dipôle exprimées en géométrie curviligne, notée
 et en géométrie cartésienne, notée
et en géométrie cartésienne, notée 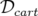 , sont reliées entre elles par l’ajout de l’application
de chaque coin du dipôle notée
, sont reliées entre elles par l’ajout de l’application
de chaque coin du dipôle notée 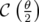 (cf. Fig. 2.2 p. §) :
(cf. Fig. 2.2 p. §) :
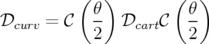 | (A.13) |
Application de transfert : En fait, l’application de transfert d’un coin dipolaire est juste le
cas limite de celle d’un dipôle secteur en géométrie curviligne (Forest, 1998, p. 368) :
 :
:
![(| (∘ ----------------------- ∘ ----------------------- )
|||xf=xi cosθ + b1 (1 + δ)2 − (pfx)2 − (piy)2 + pix sin θ − (1 + δ)2 − (pix)2 − (piy)2cosθ
||| (1∘ ----------------------- )
||||pfx=pixcos θ + (1 + δ)2 − (pix)2 − (piy)2 − b1xi sinθ
||| i [ ] i
{yf=yi + py- arcsin √----pix----- − arcsin√-----pfx----- + pyθ
| b1 (1+δ)2−(piy)2 (1+δ)2− (piy)2 b1
|||pf=pi
|||y y [ i f ]
||||lf=li + (1+-δ) arcsin √----px2---i2 − arcsin√----px2---i2 + (1+δ)θ
||| b1 (1+δ)−(py) (1+δ)− (py) b1
(δf= δ](these2525x.png) | (A.14) |
Description et Hamiltonien : Dans cette partie, nous considérons un dipôle combiné de
gradient quadripolaire 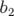 , de courbure
, de courbure 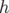 et de longueur
et de longueur 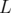 . Son Hamiltonien développé à l’ordre
deux en les impulsions est (cf. Eq. 2.41) :
. Son Hamiltonien développé à l’ordre
deux en les impulsions est (cf. Eq. 2.41) :
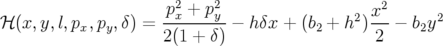 | (A.15) |
Les équations du mouvement (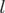 est cyclique) :
est cyclique) :
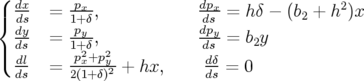 | (A.16) |
Hypothèses de calcul : Les approximations (a) des grandes machines, (b) des petits angles et (c) hard-edge ont été faites pour établir l’expression A.15 qui est complètement intégrable.
Application de transfert : Si l’on ne considère que les équations horizontales, on obtient une équation différentielle du second ordre de type oscillateur harmonique :
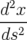 | = 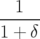 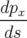 = = 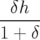 − −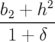 x x | ||
| alors : | |||
| xf | =  | (A.17) | |
avec ωx+ =  et ωx− = et ωx− = 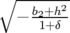 | |||
| px f | = 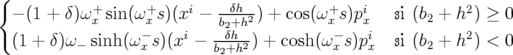 | (A.18) | |
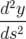 | = 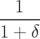 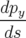 = = 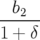 y y | ||
| alors : | |||
| yf | = 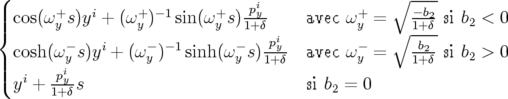 | (A.19) | |
| et : | |||
| pyf | = 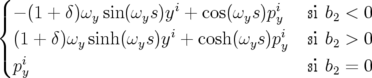 | (A.20) | |
Hamiltonien : son expression est obtenue en posant  dans le Hamiltonien 1.36 :
dans le Hamiltonien 1.36 :
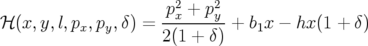 | (A.21) |
avec  la force dipolaire.
la force dipolaire.
 | (A.22) |
Hypothèses de calcul : Les approximations (a) des grandes machines, (b) des petits angles et (c) hard-edge ont été faites pour établir l’expression A.22 qui est complètement intégrable.
Application de transfert : L’intégration des équations du mouvement est immédiate :
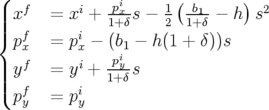 | (A.23) |
Description et Hamiltonien : Pour les machines à faible rayon de courbure comme Super-ACO,
le terme hexapolaire 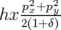 dit des petites machines ne peut plus être négligé. En particulier, il
doit être pris en compte pour les calculs de chromaticité. Le Hamiltonien d’un dipôle simple est
obtenu à partir des équations 1.36 et 1.51 :
dit des petites machines ne peut plus être négligé. En particulier, il
doit être pris en compte pour les calculs de chromaticité. Le Hamiltonien d’un dipôle simple est
obtenu à partir des équations 1.36 et 1.51 :
 |
Je vais maintenant présenter un schéma d’intégration symplectique avec correcteur.
Hypothèses de calcul : (a) l’approximation des petits angles et (b) hard-edge sont réalisées pour établir cet Hamiltonien.
Les équations du mouvement se réduisent à (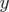 et
et  sont cycliques) :
sont cycliques) :
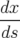 | = (1 + hx)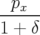 | 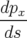 | = −h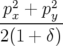 + hδ + hδ | (A.24a) |
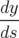 | = (1 + hx)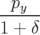 |  | = 0 | (A.24b) |
 | = −(1 + hx) − hx − hx |  | = 0 | (A.24c) |
On a immédiatement  , puis pour
, puis pour  (Eq. A.24a) :
(Eq. A.24a) :
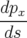 | = −h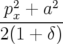 avec a2 = (p
yi)2 − 2(1 + δ)δ > 0 avec a2 = (p
yi)2 − 2(1 + δ)δ > 0 | ||
| ∫ |  = ∫
− = ∫
−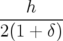 ds ds | ||
| en utilisant la primitive usuelle : | |||
∫
 | =  arctan arctan  + + 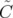 , , 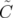 ∈ ℝ ∈ ℝ | ||
| on a alors : | |||
arctan  | = arctan  − − s s | ||
| en utilisant : | |||
| tan(a + b) | =  , , | ||
| on obtient : | |||
pxf = a![[pix − atan θ]
-----i------
a + pxtan θ](these2581x.png) | (A.25) | ||
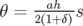 et
et  .
.
L’équation A.24a pour  peut être maintenant intégrée :
peut être maintenant intégrée :
![|-------------------------------------------------------------------|
| ( ( i)2 ) [ ( i )] |
yf = yi + 1 + px- (h−1 + xi) θ − sin θcos θ − 2arctan px- |
| a a |
---------------------------------------------------------------------](these2593x.png) | (A.27) |
Dans le cas 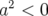 , les équations A.25 à A.27 deviennent :
, les équations A.25 à A.27 deviennent :
| |1 + hxf | | = ![{ |1 + hxi|--C+---(u++1-)2- si p ∈] − |a|,|a|[
(1+C+− )2 −u+ 2 x
|1 + hxi|(1−CC−)2 (u-u−−1) si px ⁄∈] − |a|,|a|[](these2595x.png) | (A.28) |
| px f | = ![{ +
a u1+u−+1- si px ∈ ] − |a|,|a|[
a 1+u-−- si p ⁄∈ ] − |a|,|a |[
u−1− x](these2596x.png) | (A.29) |
| yf | = ![( [ ]
{ yi + piy|1 + hxi|--C++-2 u+ − C+ − 1+ + -1+-+ 2 ln |u++-| si px ∈] − |a|,|a|[
ahi (1+C− ) [ u C C− ]
( yi + payh|1 + hxi|(1−CC−)2 u− − C− − 1u−-+ C1−-− 2 ln|uC−-| si px ⁄∈ ] − |a|,|a|[](these2597x.png) | (A.30) |
 ,
,  ,
, 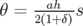 et
et  .
.
Il n’y a qu’une seule équation à intégrer, car toutes les autres variables canoniques sont des constantes du mouvement :
 | (A.31) |
Le calcul du correcteur est relativement aisé, il s’exprime par :
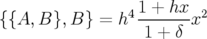 | (A.32) |
On obtient alors l’application recherchée :
 | (A.33) |
Un élément magnétique peut dévié de son emplacement théorique en position  et en
moments
et en
moments 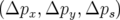 . En suivant l’approche développée par Forest et Hirata (1992), ces
défauts peuvent se modéliser de manière extrêmement simple.
. En suivant l’approche développée par Forest et Hirata (1992), ces
défauts peuvent se modéliser de manière extrêmement simple.
|
|
Par exemple, le schéma A.1 illustre la rotation d’un angle  d’un élément dans le plan x-z. L’application
de transfert de l’élément tourné, notée
d’un élément dans le plan x-z. L’application
de transfert de l’élément tourné, notée  , est obtenue comme la composition de trois applications
de base1
(Forest, 1998, chapitre 10) :
, est obtenue comme la composition de trois applications
de base1
(Forest, 1998, chapitre 10) :
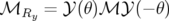 | (A.34) |
où 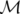 est l’application de transfert de l’élément et
est l’application de transfert de l’élément et 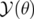 l’application décrivant une rotation
d’axe
l’application décrivant une rotation
d’axe 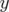 et d’angle
et d’angle 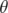 .
.
L’application 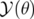 peut être considérée comme une rotation de générateur
peut être considérée comme une rotation de générateur 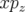 , soit (op.
cit.) :
, soit (op.
cit.) :
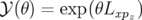 | (A.35) |
avec  et
et  la dérivée de Lie.
la dérivée de Lie.
L’évaluation de l’opérateur A.35 est obtenue en posant  dans le cas du dipôle exact en
géométrie curviligne (Eq. A.6 à A.10), dit différemment elle correspond à l’application de transfert
d’une section droite exprimée en géométrie curviligne. Cette application a été introduite la
première fois par Dragt (1982) :
dans le cas du dipôle exact en
géométrie curviligne (Eq. A.6 à A.10), dit différemment elle correspond à l’application de transfert
d’une section droite exprimée en géométrie curviligne. Cette application a été introduite la
première fois par Dragt (1982) :
 | (A.36) |
avec 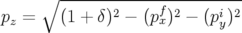 . On remarquera que les applications A.36 et A.14 sont
identiques.
. On remarquera que les applications A.36 et A.14 sont
identiques.
Une rotation d’axe  serait modélisée par l’opérateur
serait modélisée par l’opérateur  . L’application
résultante est la même que celle obtenue pour
. L’application
résultante est la même que celle obtenue pour 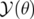 en inversant les rôles de
en inversant les rôles de  et
et  , et de
, et de 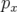 et
et
 dans les formules A.36. Enfin, une rotation d’axe
dans les formules A.36. Enfin, une rotation d’axe  a pour générateur
a pour générateur  , donc
, donc
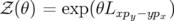 .
.
De manière similaire pour un défaut d’alignement horizontal  , l’application de transfert
, l’application de transfert
 d’un élément sera modélisée par la composition de trois applications comme (Forest, 1998,
chapitre 10) :
d’un élément sera modélisée par la composition de trois applications comme (Forest, 1998,
chapitre 10) :
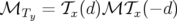 | (A.37) |
avec 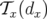 l’opérateur de translation dont le générateur est
l’opérateur de translation dont le générateur est 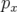 :
:
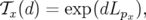 | (A.38) |
et 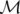 est l’application de transfert de l’élément parfait.
est l’application de transfert de l’élément parfait.
Les translations verticale et longitudinale ont pour générateurs respectivement 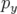 et
et  ,
soit :
,
soit :
| 𝒯y(d) | = exp(dLpy), | (A.39) |
| 𝒯z(d) | = exp(dLpz), | (A.40) |