Chapitre 1
Dynamique d’un accélérateur circulaire
1.1 Présentation
1.1.1 Introduction
Ce chapitre a pour objectif de définir les notions de base de physique des accélérateurs circulaires.
Cet exposé est loin d’être exhaustif ; le lecteur pourra se référer à des ouvrages classiques, par
exemple (Wiedemann, 1993) et (Lee, 1998) pour une introduction complète sur la physique des
accélérateurs ainsi que le Handbook of Accelerator Physics and Engineering édité par Chao et
Tigner (1998) rassemblant les principales formules de bases et surtout de nombreuses
références précieuses et utiles. La lecture des articles et ouvrages de référence de Courant
et Snyder (1958), Bruck (1966) et Sands (1970) ont également guidé l’écriture de ce
chapitre.
Après une introduction qualitative aux principaux phénomènes mis en jeu pour stocker un
faisceau de particules, je définirai de manière rigoureuse l’expression du Hamiltonien la plus
générale pour un accélérateur de particules. Cette formulation sera utile pour aborder le second
chapitre où est construit un intégrateur des équations du mouvement (section 1.2). Je rappellerai
ensuite succinctement les résultats principaux en approximation linéaire (section 1.3.1). Enfin, je
discuterai de quelques grandeurs fondamentales utilisées pour définir les performances d’une source
de lumière (section 1.4).
1.1.2 Description générale
Un anneau de stockage est une structure magnétique circulaire dans laquelle on accumule un
faisceau intense de particules. Tout l’enjeu est de pouvoir conserver ce faisceau pendant plusieurs
heures voire dizaines d’heures. Pour que le faisceau conserve de bonnes propriétés (taille,
divergence, cohérence), un vide poussé doit exister dans l’anneau. Suivant le type de particules et
les caractéristiques de l’anneau de stockage, le faisceau sera utilisé soit pour réaliser des collisions
entre particules (e.g. le défunt anneau de collision LEP et le futur collisionneur LHC du CERN),
soit pour produire de la lumière (e.g. les sources de rayonnement synchrotron de Grenoble (ESRF),
de Berkeley (ALS), la future source de lumière de troisième génération SOLEIL (Saclay)). Dans le
premier cas, le domaine d’application est principalement la physique des hautes énergies (particules,
ions lourds) ; les sources de lumières sont, quant à elles, utilisées comme microscopes géants
aux propriétés inégalées dans les domaines de la recherche fondamentale et appliquée
(biologie, propriétés structurales et électroniques de la matière, environnement, applications
industrielles).
Plongeons à présent au cœur d’un anneau de
stockage :
- Un paquet d’électrons d’énergie nominale est injecté dans la chambre à vide de
l’accélérateur (cf. Fig. 1.1). Les électrons y circulent à une vitesse proche de celle
de la lumière. Un champ magnétique guide les particules tout au long de l’anneau
autour d’une orbite fermée de référence. Il focalise les particules et leur imprime un
mouvement quasi-périodique radial et vertical autour de cette orbite fermée. On parle
alors d’oscillations bétatrons.
- Dans le cadre d’une machine circulaire idéale, nous pouvons associer une fonction spécifique à
chaque type d’éléments magnétiques. Chacun des
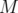 dipôles courbe la trajectoire du
faisceau d’un angle
dipôles courbe la trajectoire du
faisceau d’un angle 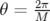 . Des quadripôles sont utilisés comme lentilles magnétiques pour
focaliser les particules. Ces deux principaux types d’éléments ainsi que la section droite
(absence de champ électromagnétique) définissent l’optique linéaire de l’anneau, en
référence à l’approximation paraxiale utilisée. L’agencement de ces éléments définit
la maille de l’accélérateur. Si l’anneau de stockage est constitué de
. Des quadripôles sont utilisés comme lentilles magnétiques pour
focaliser les particules. Ces deux principaux types d’éléments ainsi que la section droite
(absence de champ électromagnétique) définissent l’optique linéaire de l’anneau, en
référence à l’approximation paraxiale utilisée. L’agencement de ces éléments définit
la maille de l’accélérateur. Si l’anneau de stockage est constitué de  secteurs
identiques appelés super-périodes, alors il possède une symétrie interne qui permet
d’augmenter la stabilité globale de la dynamique (ce point sera abordé dans la
section 1.4).
secteurs
identiques appelés super-périodes, alors il possède une symétrie interne qui permet
d’augmenter la stabilité globale de la dynamique (ce point sera abordé dans la
section 1.4).
- Durant chaque révolution, un électron perd une partie de son énergie sous forme de
rayonnement synchrotron. Afin de stocker les électrons pendant plusieurs heures, il est
nécessaire de compenser en moyenne cette perte d’énergie. C’est le rôle des cavités
radiofréquences qui accélèrent longitudinalement la particule qui les traverse.
- Cette accélération périodique a pour effet de regrouper les électrons en paquets. Dans chaque
paquet, les électrons oscillent en longitude et en énergie par rapport à une particule de
référence située au centre du paquet (cf. Fig. 1.2). Ces oscillations sont appelées oscillations
synchrotrons.
- La combinaison perte d’énergie par rayonnement synchrotron et apport d’énergie des cavités
RF induit un lent amortissement radiatif des amplitudes d’oscillation des particules : la
trajectoire de chaque électron tend vers celle d’une particule de référence située au centre du
paquet.
- L’amortissement des oscillations est arrêté par les fluctuations quantiques. Ce phénomène est
lié à la quantification du rayonnement émis par les électrons et a tendance à exciter
continûment les oscillations des particules : le faisceau atteint alors ses dimensions d’équilibre.
Les particules ont leurs phases et amplitudes d’oscillations distribuées suivant une loi de
Gauss transversalement et longitudinalement.
- Pour chaque degré de liberté, il existe une amplitude maximale d’oscillation au-delà de
laquelle le mouvement devient instable. Cette amplitude définit l’acceptance du faisceau.
L’amplitude limite peut être due à un élément physique qui arrête les électrons (e.g. les
parois de la chambre à vide) ou à un effet nonlinéaire du champ électromagnétique conduisant
à la divergence des trajectoires.
- Les électrons peuvent également être perdus suite à des diffusions sur les atomes du gaz
résiduel présent dans la chambre à vide ou en raison des fluctuations statistiques induites par
l’amortissement radiatif et l’excitation quantique.
- Pour être complet, il faut dire quelques mots sur les effets collectifs. Typiquement un
paquet est constitué d’un milliard d’électrons. Les électrons peuvent interagir entre
eux : lors de diffusions simples ou multiples, les électrons peuvent acquérir des
amplitudes d’oscillation plus grandes que l’acceptance du faisceau. Les électrons peuvent
également se mettre à osciller de manière cohérente ce qui, dans certains cas, conduit à
l’instabilité.
L’objectif de la section suivante est d’établir l’expression générale du Hamiltonien d’une
particule relativiste se déplaçant dans un champ électromagnétique. Nous pourrons alors en déduire
les équations du mouvement et discuter de la dynamique linéaire et nonlinéaire d’une particule
circulant dans un anneau de stockage.
1.2 Formulation hamiltonienne
Pour établir les équations du mouvement d’une particule circulant dans un accélérateur, nous
partirons du principe de moindre action. Nous commencerons par établir l’expression du Lagrangien
d’une particule libre relativiste de masse 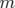 , puis nous plongerons la particule de charge
, puis nous plongerons la particule de charge  dans
un champ électromagnétique (section 1.2.1). Nous en déduirons l’expression générale du
Hamiltonien relativiste que nous exprimerons en coordonnées de l’accélérateur (section 1.2.2). A
chaque étape, nous définirons avec précision l’ensemble des hypothèses réalisées et l’expression
générale du champ magnétique (section 1.2.3).
dans
un champ électromagnétique (section 1.2.1). Nous en déduirons l’expression générale du
Hamiltonien relativiste que nous exprimerons en coordonnées de l’accélérateur (section 1.2.2). A
chaque étape, nous définirons avec précision l’ensemble des hypothèses réalisées et l’expression
générale du champ magnétique (section 1.2.3).
1.2.1 Lagrangien relativiste
Soit  l’intégrale d’action pour une particule libre relativiste,
l’intégrale d’action pour une particule libre relativiste, 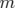 sa masse,
sa masse, 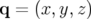 son
vecteur position et
son
vecteur position et  son vecteur vitesse. Par application du principe de relativité,
l’action doit être indépendante du choix du référentiel d’inertie, soit un invariant de
Lorentz : l’intégrale d’action
son vecteur vitesse. Par application du principe de relativité,
l’action doit être indépendante du choix du référentiel d’inertie, soit un invariant de
Lorentz : l’intégrale d’action 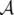 est donc un scalaire. De plus, il ne doit figurer que des
différentielles du premier degré sous le signe d’intégration (cf. Landau et Lifchitz, Physique
théorique : Théorie des Champs, chap. I et II). La seule solution pour une particule
libre est alors l’intervalle relativiste
est donc un scalaire. De plus, il ne doit figurer que des
différentielles du premier degré sous le signe d’intégration (cf. Landau et Lifchitz, Physique
théorique : Théorie des Champs, chap. I et II). La seule solution pour une particule
libre est alors l’intervalle relativiste 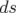 à une constante de proportionnalité près, notée
à une constante de proportionnalité près, notée
 .
.
Si l’intégrale est prise sur une ligne d’univers s’étendant entre deux événements  et
et 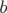 qui
sont les positions initiale et finale de la particule aux instants respectifs
qui
sont les positions initiale et finale de la particule aux instants respectifs 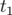 et
et 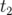 , alors l’action
, alors l’action  s’écrit :
s’écrit :
 | (1.1) |
Or l’intervalle relativiste 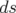 est donné par la métrique de Minkowski :
est donné par la métrique de Minkowski :
 | (1.2) |
où  est la vitesse de la lumière ; donc l’action 1.1 peut se réécrire :
est la vitesse de la lumière ; donc l’action 1.1 peut se réécrire :
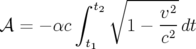 | (1.3) |
Par définition du Lagrangien (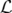 ), l’action est également définie par la relation (cf. Landau et
Lifchitz, Physique théorique : Mécanique, chap. I) :
), l’action est également définie par la relation (cf. Landau et
Lifchitz, Physique théorique : Mécanique, chap. I) :
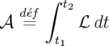 | (1.4) |
On déduit des équations 1.3 et 1.4 l’expression du Lagrangien :
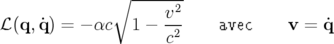 | (1.5) |
La constante  est déterminée en passant à la limite
est déterminée en passant à la limite  qui doit redonner l’énergie
cinétique classique pour une particule libre ; en effectuant un développement limité à l’ordre un de
l’expression 1.5, on obtient :
qui doit redonner l’énergie
cinétique classique pour une particule libre ; en effectuant un développement limité à l’ordre un de
l’expression 1.5, on obtient :
![1 v2 v4 1
ℒ (q,q˙) −−−−→ ℒclassique ⇐ ⇒ − αc + --α---+ 𝒪 (-3-) = [− mc2 ] +-mv2
c→+ ∞ 2 c c 2](these37x.png) | (1.6) |
d’où  . Le terme entre crochets est constant donc il n’intervient pas dans les équations du
mouvement : il correspond à l’énergie de masse de la particule.
. Le terme entre crochets est constant donc il n’intervient pas dans les équations du
mouvement : il correspond à l’énergie de masse de la particule.
Le Lagrangien d’une particule libre relativiste de masse 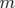 s’exprime finalement
par :
s’exprime finalement
par :
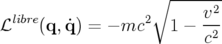 | (1.7) |
Pour une particule relativiste de charge  en mouvement dans un champ électromagnétique, le
Lagrangien total comporte un terme supplémentaire (
en mouvement dans un champ électromagnétique, le
Lagrangien total comporte un terme supplémentaire ( ) caractérisant l’interaction de la
particule avec le champ électromagnétique
) caractérisant l’interaction de la
particule avec le champ électromagnétique 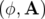 (voir Landau et Lifchitz, Théorie des Champs,
chap. III) :
(voir Landau et Lifchitz, Théorie des Champs,
chap. III) :
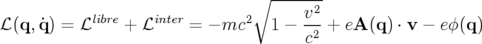 | (1.8) |
avec 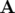 le potentiel vecteur et
le potentiel vecteur et 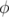 le potentiel scalaire solutions des équations de Maxwell.
le potentiel scalaire solutions des équations de Maxwell.
1.2.2 Hamiltonien relativiste
1.2.2.1 Moments canoniques
Par définition, les moments canoniques  s’obtiennent à partir du Lagrangien :
s’obtiennent à partir du Lagrangien :
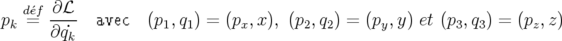 | (1.9) |
soit en utilisant l’expression 1.8 et le facteur de Lorentz 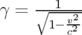 :
:
 | (1.10) |
Le Hamiltonien autonome 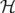 est obtenu à partir de la fonction de Lagrange 1.8 (voir Landau et
Lifchitz, Mécanique, chap. VII) :
est obtenu à partir de la fonction de Lagrange 1.8 (voir Landau et
Lifchitz, Mécanique, chap. VII) :
| ℋ(q,p) | 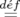 ∑
k ∑
k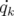  −ℒ(q, −ℒ(q,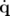 ) ) | |
|
| = γmv2 + eA ⋅ v − | |
|
| = γmc2 + eϕ(q) | (1.11) |
En introduisant l’impulsion mécanique 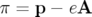 , on établit à partir des équations 1.10 et 1.11
la relation :
L’expression du Hamiltonien 1.11 devient en utilisant la relation 1.12 :
, on établit à partir des équations 1.10 et 1.11
la relation :
L’expression du Hamiltonien 1.11 devient en utilisant la relation 1.12 :
 | (1.13) |
Les équations du mouvement sont les équations dites de Hamilton ou canoniques :
 | (1.14) |
avec la relation supplémentaire si le Hamiltonien dépend explicitement du temps 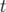 :
:
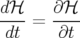 | (1.15) |
Les variables 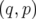 sont appelées variables canoniques. Pour une description du formalisme
Hamiltonien, le lecteur pourra se reporter par exemple au chapitre VII du tome de Mécanique de
Landau et Lifchitz.
sont appelées variables canoniques. Pour une description du formalisme
Hamiltonien, le lecteur pourra se reporter par exemple au chapitre VII du tome de Mécanique de
Landau et Lifchitz.
1.2.2.2 Définition des coordonnées de l’accélérateur
Pour la suite de l’exposé, il est utile d’obtenir une expression du Hamiltonien pour les jeux de
coordonnées cartésiennes et curvilignes. L’obtention générale du Hamiltonien va être présentée en
coordonnées curvilignes dont les coordonnées cartésiennes ne sont qu’un cas particulier (la courbure
et la torsion sont nulles, cf. infra).
Les coordonnées curvilignes, notées  , sont définies par rapport au repère de
Serret-Frenet direct
, sont définies par rapport au repère de
Serret-Frenet direct 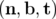 ; une particule de coordonnées transverses
; une particule de coordonnées transverses  et
et  est repérée par son vecteur position
est repérée par son vecteur position  par rapport à l’orbite de référence
par rapport à l’orbite de référence  (voir
Fig. 1.3) :
(voir
Fig. 1.3) :
| r(X,Y,s) | = r0(s) + Xn(s) + Y b(s) | (1.16)
|
| = xi + yj + zk | | |
Les vecteurs orthonormés  sont respectivement les vecteurs tangent, normal et binormal
définis par :
sont respectivement les vecteurs tangent, normal et binormal
définis par :
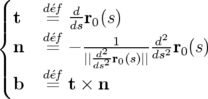 | (1.17) |
où  et
et  décrivent la courbure et la torsion locales de la trajectoire à la longitude
décrivent la courbure et la torsion locales de la trajectoire à la longitude
 :
:
Je rappelle les formules de Frenet :
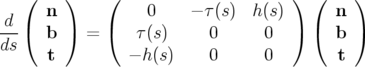 | (1.18) |
On recherche une transformation canonique entre les anciennes variables notées
 et les nouvelles variables
et les nouvelles variables  .
Pour cela, on construit une fonction génératrice dépendant des anciens moments et des
nouvelles positions,
.
Pour cela, on construit une fonction génératrice dépendant des anciens moments et des
nouvelles positions, 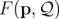 . Les changements de variables sont alors définis implicitement
par :
. Les changements de variables sont alors définis implicitement
par :
| q |  − −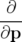 F(p, F(p, ) ) | (1.19a)
|
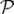 |  − −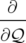 F(p, F(p,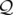 ) ) | (1.19b) |
L’équation 1.19a s’intègre simplement en utilisant la relation 1.16.
 | (1.20) |
Par convention la fonction 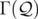 est choisie nulle. L’équation 1.19b définit les nouveaux moments
recherchés :
est choisie nulle. L’équation 1.19b définit les nouveaux moments
recherchés :
avec 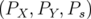 les projections usuelles de l’impulsion sur la base
les projections usuelles de l’impulsion sur la base 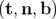 . On note également
que les coordonnées du potentiel vecteur
. On note également
que les coordonnées du potentiel vecteur 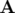 se transforment comme celles du moment
se transforment comme celles du moment  (cf.
équation 1.10).
(cf.
équation 1.10).
Dans la suite, on fait l’hypothèse que la trajectoire de référence est plane, i.e. que la torsion  est nulle.
En remarquant que la base de Serret-Frenet est orthonormée, le nouveau Hamiltonien s’écrit en
utilisant l’expression 1.13 :
est nulle.
En remarquant que la base de Serret-Frenet est orthonormée, le nouveau Hamiltonien s’écrit en
utilisant l’expression 1.13 :
| ℋ | (X,Y,s,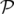 X, X, Y , Y ,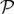 s) = ℋ(q( s) = ℋ(q(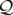 , ,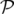 ), p( ), p( , , )) )) | |
|
| = c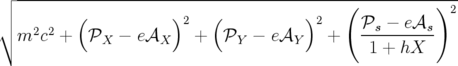 + eϕ( + eϕ(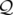 ) ) | (1.21) |
L’expression 1.21 va être réécrite sous une forme plus standard pour la physique des accélérateurs
au moyen de trois transformations canoniques (cf. Dragt et Forest, 1986).
1.2.2.3 Changement de variable indépendante
Dans un accélérateur, il est plus commode d’exprimer la trajectoire d’une particule en fonction de la
coordonnée longitudinale prise comme variable indépendante à la place du temps  (
( en
coordonnées rectangulaires ou
en
coordonnées rectangulaires ou  en coordonnées curvilignes).
en coordonnées curvilignes).
Comme nouveau Hamiltonien,
on choisit 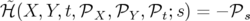 en notant
en notant 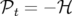 :
:
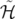 (X, Y,t, (X, Y,t,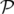 X, X,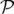 Y , Y ,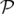 t) = t) = | − (1 + hX) | |
|
| − e s s | (1.22) |
On vérifie a posteriori que 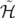 conjugue les couples de variables
conjugue les couples de variables 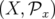 ,
, 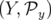 et
et
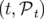 :
:
d t t − dℋ = − dℋ = | −∑
k=12 − −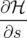 ds − ds −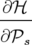 d d s − s − dt dt | |
|
⇒−d s s d d = = | ∑
k=12![[ ]
( ∂ℋ ) ( ∂ℋ ) −1 ( ∂ ℋ ) ( ∂ ℋ ) −1
----- ---- d𝒬k + ----- ---- d𝒫k
∂ 𝒬k ∂𝒫s ∂𝒫k ∂𝒫s](these134x.png) | |
|
| +  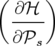 −1dt + −1dt +  −1d −1d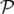 t
t | (1.23)
|
| par identification en utilisant les équations 1.14, on obtient les nouvelles équations de
Hamilton : |
|
|
| 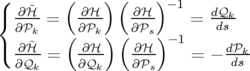 pour k = 1, 2 pour k = 1, 2 | (1.24)
|
| et |
|
|
|  | (1.25) |
La variable  est physiquement reliée à la notion de temps de vol et son moment canonique
est physiquement reliée à la notion de temps de vol et son moment canonique 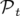 est
l’opposé de l’énergie totale de la particule. Pour la suite des calculs, on suppose que le potentiel électrique
est
l’opposé de l’énergie totale de la particule. Pour la suite des calculs, on suppose que le potentiel électrique
 est nul.
est nul.
En faisant l’hypothèse que le potentiel vecteur est nul le long de l’axe optique, i.e. 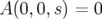 ,
on constate l’existence de la trajectoire particulière :
,
on constate l’existence de la trajectoire particulière : 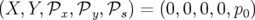 , que l’on
appelle trajectoire de référence.
, que l’on
appelle trajectoire de référence.
1.2.2.4 Changement d’échelle
La seconde transformation revient simplement à introduire un facteur d’échelle dans les
variables :
  | | (1.26) |
Pour conserver la nature hamiltonienne des équations, le nouveau Hamiltonien est simplement
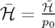 , soit :
, soit :
 | (1.27) |
avec 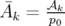 . Le long de la trajectoire de référence, on a alors :
. Le long de la trajectoire de référence, on a alors :
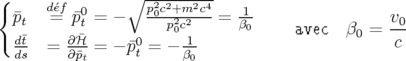 | (1.28) |
1.2.2.5 Expression finale du Hamiltonien à trois degrés de liberté
Usuellement, on préfère définir le mouvement d’une particule par rapport à une trajectoire de
référence nulle, ce qui nous conduit à faire le dernier changement de variables dépendant de  (d’après Eq. 1.28) :
(d’après Eq. 1.28) :
 | (1.29) |
Ce changement de variables dépend explicitement de  . Si
. Si  est une fonction génératrice, le
nouveau Hamiltonien sera donné par :
est une fonction génératrice, le
nouveau Hamiltonien sera donné par :  . Nous construisons la fonction génératrice
dépendant des anciennes positions et des nouveaux moments
. Nous construisons la fonction génératrice
dépendant des anciennes positions et des nouveaux moments 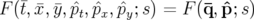 (Dragt et Forest, 1986) :
(Dragt et Forest, 1986) :
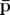 | = 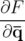  F( F(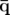 , , ; s) = ; s) = 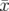 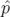 x + x + 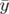 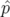 y + y + 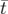 ( (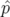 t + t +  ) + G( ) + G(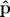 ,s) ,s) | (1.30)
|
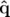 | = 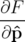  F( F(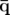 , ,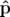 ; s) = ; s) =  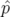 x + x + 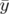  y + y +  ( (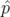 t + t +  ) + ) + 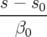  t + K(s) t + K(s) | (1.31) |
La fonction  est a priori une fonction quelconque. Pour permettre des comparaisons avec la
littérature, elle est choisie telle que :
est a priori une fonction quelconque. Pour permettre des comparaisons avec la
littérature, elle est choisie telle que :
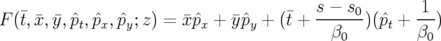 | (1.32) |
On en déduit l’expression du nouveau Hamiltonien  :
:
 | (1.33) |
en remarquant l’identité :  .
.
1.2.2.6 Approximations
Dans le cas ultra-relativiste, le Hamiltonien 1.33 se simplifie
encore
puisque  et
et  . Pour alléger l’écriture, les variables « perdent leur chapeau » (si
aucune confusion n’est possible) et on pose
. Pour alléger l’écriture, les variables « perdent leur chapeau » (si
aucune confusion n’est possible) et on pose  et
et  :
:
 | (1.34) |
Interprétons physiquement les nouvelles variables  et
et  :
:
 représente l’écart à énergie nominale
représente l’écart à énergie nominale  normalisée par l’énergie de la
particule nominale ultra-relativiste.
normalisée par l’énergie de la
particule nominale ultra-relativiste.
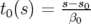 est le temps de passage en
est le temps de passage en  de la particule synchrone. On suppose
que cette dernière se trouve en
de la particule synchrone. On suppose
que cette dernière se trouve en  en
en  . Si
. Si 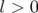 ,
, 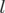 représente l’avance de la
particule par rapport à la particule synchrone.
représente l’avance de la
particule par rapport à la particule synchrone.
Lorsqu’on ne s’intéresse pas au cas du solénoïde, le potentiel vecteur n’a qu’une seule
composante non nulle  qui ne dépend que des coordonnées transverses :
qui ne dépend que des coordonnées transverses :
 | (1.35) |
Pour la suite du travail, on a le choix entre conserver cette expression avec la racine
carrée et effectuer un développement limité. Dans ce dernier cas, le Hamiltonien se réduit
à :
| ℋ | = −(1 + hx)(1 + δ)(1 −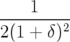 (px2 + p
y2)) − eÂ
s + δ + 1 (px2 + p
y2)) − eÂ
s + δ + 1 | |
|
| = (1 + hx) − (1 + hx)(1 + δ) − eÂs + δ + 1 − (1 + hx)(1 + δ) − eÂs + δ + 1 | | |
soit finalement :
 | (1.36) |
Cette dernière expression sera utilisée pour déduire la dynamique linéaire. Pour l’instant, il ne reste
plus qu’à déterminer l’expression du potentiel vecteur.
1.2.3 Potentiel vecteur
L’expression la plus générale du potentiel vecteur est calculée en partant des équations de Maxwell
exprimées dans le vide et pour un champ électromagnétique statique en coordonnées curvilignes
(Lee, 1998) :
| ∇ × B = 0, | ∇⋅ B = 0 | (1.37)
|
⇐⇒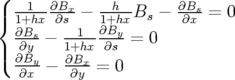 , , | 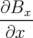 + + 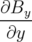 + + 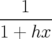 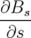 + + 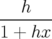 Bx = 0 Bx = 0 | (1.38) |
La divergence nulle (Eq. 1.37) implique l’existence d’un potentiel vecteur 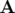 vérifiant, à une
condition de jauge près :
vérifiant, à une
condition de jauge près :  .
.
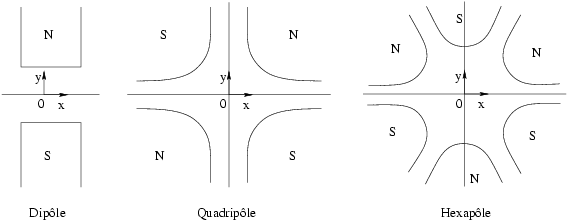
En prenant l’hypothèse que le plan  est un plan d’antisymétrie pour le champ magnétique
(cf. symétrie des aimants, Fig. 1.4), alors :
est un plan d’antisymétrie pour le champ magnétique
(cf. symétrie des aimants, Fig. 1.4), alors :
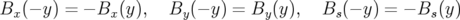 | (1.39) |
Le champ magnétique peut alors être développé en série des variables transverses sous la
forme (Voir Steffen, 1985 et pour une représentation plus complète, Papaphilippou et al.,
2001) :
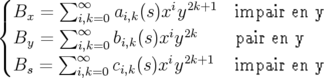 | (1.40) |
où les coefficients 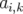 ,
, 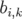 ,
, 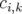 des fonctions de
des fonctions de  à déterminer.
à déterminer.
En injectant les solutions 1.40 dans les équations de Maxwell 1.38, on obtient les formules de
récurrence (Steffen, 1985) :
![( a′ = (i + 1)[c + hc ]
|||{ i,k i,k i− 1,k
ai,k = 2i+k1+1bi+1,k
| b′ = (2k + 1)[c + hc ]
||( i′,k i,k i−1,k
ci,k = − 2(k + 1)[bi,k+1 + hbi−1,k+1] − (i + 1)[ai+1,k + hai,k]](these227x.png) | (1.41) |
avec la dérivée par rapport à  notée
notée  et par convention d’écriture un coefficient ayant un de ses
indices négatif est nul.
et par convention d’écriture un coefficient ayant un de ses
indices négatif est nul.
Si le champ magnétique 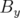 est mesuré en tant que fonction des coordonnées
est mesuré en tant que fonction des coordonnées 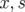 dans le plan
d’antisymétrie sous la forme :
dans le plan
d’antisymétrie sous la forme :
 | (1.42) |
alors  (cf. Eq. 1.40) et en utilisant les relations de récurrence 1.41, on déduit, après
quelques lignes de calcul, l’expression générale du champ magnétique (Lee, 1998) :
(cf. Eq. 1.40) et en utilisant les relations de récurrence 1.41, on déduit, après
quelques lignes de calcul, l’expression générale du champ magnétique (Lee, 1998) :
![(
||Bx = B1,{0y + 2B2,0xy + 3B3,0x2y− }
|||| 1 hB1,0- B0′′,0 1 ′′ ′ ′ 3
||| 3 3B3,0 + 2hB2,0 − h(B2,0 + 2′′+ 2 ) + 2 [B 1,0 − (hB 0,0)] y + ...
|{By = B0,0 + B1,0x + B2,0x2 − (B2,0 + B0,0-+ hB1,0)y2 + B3,0x3−
{ hB1,02 B′′0,0 2 1 }
||| 3B3,0 + 2hB2,0 − h (B2,0 + --2--+ -2-) + 2[B ′1′,0 − (hB ′0,0)′] xy2 + ...
||| ′ ( ′ ′ ) ′ ′ 2 ′ 2
||||Bs = B 0,0(y + B1,0 −′hB 0,0′′′x)y + (B 2,0 − hB 1,0 + h B 0,0)x y
( − 13 B2′,0 + hB21,0+ B12,0- y3 + ...](these234x.png) | (1.43) |
Lorsque  (élément rectangulaire), le champ magnétique peut s’écrire à partir de
l’expression 1.43 en représentation complexe :
(élément rectangulaire), le champ magnétique peut s’écrire à partir de
l’expression 1.43 en représentation complexe :
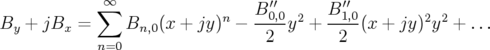 | (1.44) |
avec  .
.
Pour simplifier les calculs, les coefficients 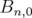 sont souvent pris constants, donc l’équation 1.44
se simplifie encore (Lee, 1998) :
sont souvent pris constants, donc l’équation 1.44
se simplifie encore (Lee, 1998) :
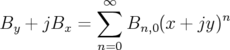 | (1.45) |
par convention, on pose  avec
avec 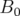 choisi tel que
choisi tel que  et avec
et avec
 où
où 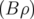 est la rigidité magnétique. Cette représentation complexe du champ
magnétique est souvent appelée représentation de Beth.
est la rigidité magnétique. Cette représentation complexe du champ
magnétique est souvent appelée représentation de Beth.
A ce stade, il existe deux conventions : la sommation de l’équation 1.45 commence à 0 aux
Etats-Unis et à 1 en Europe. Dans la suite, je prendrai la convention européenne, donc
l’équation 1.45 devient :
| By + jBx | = B0 ∑
n=1∞(b
n + jan)(x + jy)n−1 | (1.46)
|
| avec |
|
|
bn = 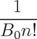 | 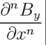 x=y=0 et an = x=y=0 et an = 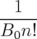 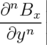 x=y=0 x=y=0 | (1.47) |
Les coefficients multipolaires 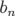 et
et 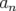 décrivent respectivement les
décrivent respectivement les 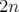 -pôles parfaits droits et
tournés.
-pôles parfaits droits et
tournés.
Le potentiel vecteur (avec 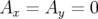 ) est lié au champ magnétique par l’équation,
) est lié au champ magnétique par l’équation,
 , soit exprimée en coordonnées curvilignes :
, soit exprimée en coordonnées curvilignes :
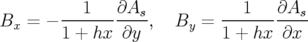 | (1.48) |
En coordonnées rectangulaires ( ), la formule 1.48 s’intègre immédiatement en utilisant
l’expression 1.46 pour donner :
), la formule 1.48 s’intègre immédiatement en utilisant
l’expression 1.46 pour donner :
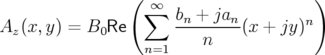 | (1.49) |
où 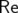 désigne la partie réelle. Deux types de représentations nous intéressent :
désigne la partie réelle. Deux types de représentations nous intéressent :
Représention curviligne : En coordonnées curvilignes, le potentiel vecteur  ne peut pas
s’exprimer de manière aussi simple qu’en coordonnées rectangulaires (cf. Eq. 1.49). La solution
s’exprime sous forme d’une série infinie qu’il faut tronquer à l’ordre
ne peut pas
s’exprimer de manière aussi simple qu’en coordonnées rectangulaires (cf. Eq. 1.49). La solution
s’exprime sous forme d’une série infinie qu’il faut tronquer à l’ordre 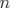 (voir par exemple la thèse
de Fartoukh, 1997). Cette description est adaptée aux éléments type dipôle de rayon de courbure
(voir par exemple la thèse
de Fartoukh, 1997). Cette description est adaptée aux éléments type dipôle de rayon de courbure
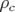 .
.
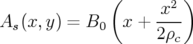 | (1.50) |
L’expression qui nous intéresse est celle de 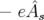 exprimée pour le Hamiltonien 1.36 ; en
utilisant la rigidité magnétique
exprimée pour le Hamiltonien 1.36 ; en
utilisant la rigidité magnétique 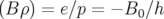 , on obtient :
, on obtient :
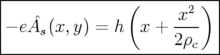 | (1.51) |
Représentation rectangulaire : Ce cas est particulièrement adapté à la description des
éléments sans courbure, i.e. les quadripôles, les hexapôles et les éléments multipolaires.
Pour le quadripôle droit et l’hexapôle droit la formule 1.49 donne respectivement :
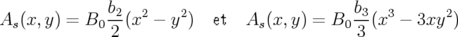 | (1.52) |
soit pour 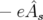 :
:
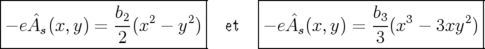 | (1.53) |
1.3 Dynamique transverse
1.3.1 Dynamique linéaire
Dans un accélérateur, la solution des équations transverses du mouvement peut se décomposer en
deux termes, (a) l’orbite fermée qui, par définition, est une orbite de période 1 et (b) une oscillation
de faible amplitude dite bétatron autour de cette orbite fermée. Nous verrons que l’orbite fermée
dépend de l’énergie de la particule. Mais tout d’abord établissons les équations linéaires du
mouvement.
Pour cela, nous partons de l’expression du Hamiltonien 1.36 que nous réécrivons en ne
conservant que les parties linéaire et quadratique du potentiel vecteur 1.46, i.e. le potentiel d’un
dipôle 1.51 et celui d’un quadripôle droit 1.53 :
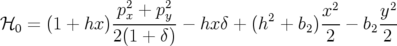 | (1.54) |
Les équations du mouvement transverse sont alors :
 | (1.55) |
Pour l’instant, nous adoptons les approximations classiques afin de retrouver les expressions
données par la littérature, à savoir :
- l’approximation des grandes machines en négligeant le terme hexapolaire
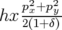 dans
l’expression du Hamiltonien 1.54
dans
l’expression du Hamiltonien 1.54
- la dépendance linéaire en l’écart en énergie
 .
.
Le Hamiltonien 1.54 devient en prenant en compte la première approximation classique :
 | (1.56) |
Les équations du mouvement 1.55 s’écrivent comme :
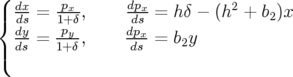 | (1.57) |
Soit en termes d’équations différentielles du second ordre des variables  et
et 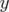 (en négligeant les
termes d’ordre 2 en
(en négligeant les
termes d’ordre 2 en 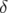 ) :
) :
 | (1.58) |
Nous remarquerons les points suivants :
- un dipôle focalise dans le plan horizontal ;
- si un quadripôle droit focalise dans un plan, alors il défocalise dans l’autre plan, car
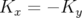 et
et  ;
;
- la focalisation dépend de l’énergie
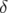 de la particule ;
de la particule ;
- les fonctions
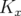 et
et 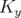 sont définies par morceaux à valeur constante dans chaque
élément magnétique et L-périodiques
pour une machine de circonférence
sont définies par morceaux à valeur constante dans chaque
élément magnétique et L-périodiques
pour une machine de circonférence 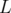 ;
;
- la solution des équations 1.58 est la somme de la solution générale de l’équation
homogène et d’une solution particulière.
Dans la suite, j’emploierai les anglicismes : particule on momemtum si  et particule off
momemtum si
et particule off
momemtum si 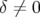 . Le symbole
. Le symbole  désigne la dérivation par rapport à la longitude
désigne la dérivation par rapport à la longitude  et
et  la
dérivée seconde.
la
dérivée seconde.
1.3.1.1 Particule on momentum
L’équation homogène du système 1.58 peut être réécrite pour  comme l’équation
générique :
comme l’équation
générique :
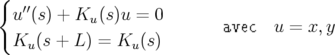 | (1.59) |
C’est donc une équation de Hill.
La solution générale 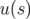 de l’équation de Hill 1.59 décrit le mouvement d’une particule
d’énergie nominale de la machine, i.e.
de l’équation de Hill 1.59 décrit le mouvement d’une particule
d’énergie nominale de la machine, i.e.  . Usuellement, la solution s’écrit de différentes
manières dans la littérature :
. Usuellement, la solution s’écrit de différentes
manières dans la littérature :
– en utilisant le théorème de Floquet (voir par exemple Courant et Snyder, 1958), la solution
s’exprime en fonction de la fonction bétatron 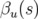 :
:
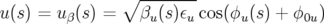 | (1.60) |
avec la phase  ,
, 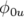 la phase à l’origine et
la phase à l’origine et 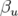 vérifiant l’équation
différentielle :
vérifiant l’équation
différentielle :
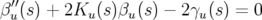 | (1.61) |
en posant  et
et  . Les paramètres
. Les paramètres  ,
, 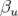 et
et 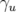 sont appelés fonctions ou
paramètres de Twiss. L’avance de phase sur un tour complet ramenée à
sont appelés fonctions ou
paramètres de Twiss. L’avance de phase sur un tour complet ramenée à 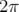 définit le nombre
d’ondes
définit le nombre
d’ondes 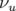 :
:
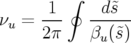 | (1.62) |
qui correspond au nombre moyen d’oscillations effectuées par la particule autour de l’orbite
fermée.
L’invariant linéaire, aussi appelé invariant de Courant-Snyder ou encore émittance, est
l’intégrale première du mouvement :
 | (1.63) |
Géométriquement, l’équation 1.63 est celle d’une ellipse d’aire  dans le plan
dans le plan  (cf.
Fig. 1.5).
(cf.
Fig. 1.5).
– en utilisant la paramétrisation de Courant-Snyder (1958) :
 | (1.64) |
où 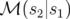 est la matrice de transfert de la longitude
est la matrice de transfert de la longitude 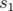 à
à 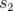 ,
,  l’avance de phase entre
l’avance de phase entre 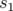 à
à 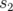 ,
, 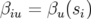 . Sur un tour complet, l’expression 1.64 se simplifie pour donner l’application
linéaire de premier retour :
. Sur un tour complet, l’expression 1.64 se simplifie pour donner l’application
linéaire de premier retour :
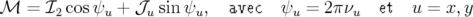 | (1.65) |
avec 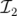 la matrice identité et
la matrice identité et
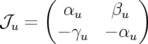 | (1.66) |
– en utilisant les fonctions principales 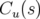 et
et 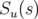 qui par définition sont deux solutions
indépendantes de l’équation de Hill 1.59 vérifiant :
qui par définition sont deux solutions
indépendantes de l’équation de Hill 1.59 vérifiant :
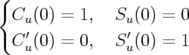 | (1.67) |
La solution générale avec pour conditions initiales  peut alors s’écrire (Courant et Snyder,
1958) :
peut alors s’écrire (Courant et Snyder,
1958) :
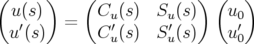 | (1.68) |
1.3.1.2 Particule off momentum
Pour une particule n’ayant pas l’énergie nominale du faisceau, i.e. 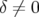 , l’équation 1.58
devient :
, l’équation 1.58
devient :
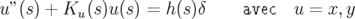 | (1.69) |
Par convention, on appelle fonction dispersion la solution particulière 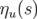 périodique pour
périodique pour
 de l’équation 1.69. En utilisant les fonctions principales
de l’équation 1.69. En utilisant les fonctions principales 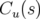 et
et  , la dispersion
linéaire est donnée par la formule (Lee, 1998) :
, la dispersion
linéaire est donnée par la formule (Lee, 1998) :
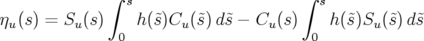 | (1.70) |
En utilisant la linéarité des équations, on en déduit que la solution complète peut s’exprimer
par :
| u(s) | =  cos(ϕu(s) + ϕu0) + ηu(s)δ cos(ϕu(s) + ϕu0) + ηu(s)δ | (1.71)
|
| = uβ(s) + uδ(s) | (1.72) |
avec  la solution bétatron et
la solution bétatron et 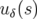 l’orbite fermée chromatique.
l’orbite fermée chromatique.
Similairement à l’optique géométrique où une lentille focalise plus faiblement les photons de
petite longueur d’onde, i.e. de grande énergie, la focalisation d’un quadripôle est une fonction
intrinsèquement dépendante de l’énergie ( ). Si
). Si 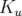 est le gradient quadripolaire, alors on peut
écrire (cf. Eq. 1.58) :
est le gradient quadripolaire, alors on peut
écrire (cf. Eq. 1.58) :
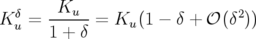 | (1.73) |
Donc, les particules ayant une énergie supérieure à l’énergie nominale 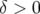 sont moins focalisées.
Il s’ensuit que l’avance de phase dans un élément quadripolaire devient une fonction de l’énergie, ce
qui nous conduit à définir la chromaticité comme la variation du nombre d’ondes,
sont moins focalisées.
Il s’ensuit que l’avance de phase dans un élément quadripolaire devient une fonction de l’énergie, ce
qui nous conduit à définir la chromaticité comme la variation du nombre d’ondes, 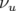 , en fonction
de l’énergie :
, en fonction
de l’énergie :
 | (1.74) |
Suivant les cas, nous parlerons de chromaticité [globale] ou de chromaticité réduite, i.e. ramenée au
nombre d’ondes  . La contribution produite uniquement par les éléments linéaires, i.e. les
dipôles et les quadripôles est appelée chromaticité naturelle. Elle est toujours négative et a des
conséquences très dommageables sur la dynamique globale du faisceau si elle n’est pas corrigée.
Par exemple pour SOLEIL, les chromaticités naturelles sont
. La contribution produite uniquement par les éléments linéaires, i.e. les
dipôles et les quadripôles est appelée chromaticité naturelle. Elle est toujours négative et a des
conséquences très dommageables sur la dynamique globale du faisceau si elle n’est pas corrigée.
Par exemple pour SOLEIL, les chromaticités naturelles sont  et
et
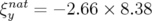 , ce qui induit pour
, ce qui induit pour  % les déplacements des nombres d’ondes proches
du demi-entier
% les déplacements des nombres d’ondes proches
du demi-entier  . Ces glissements des nombres d’ondes peuvent amener le
faisceau sur des lignes de résonance et conduire à des conséquences néfastes pour les performances
de l’anneau.
. Ces glissements des nombres d’ondes peuvent amener le
faisceau sur des lignes de résonance et conduire à des conséquences néfastes pour les performances
de l’anneau.
La seconde raison nécessitant une correction de chromaticité provient des effets collectifs.
Lorsqu’un paquet de particules circule dans l’accélérateur, les particules de tête laissent derrière
elles un champ de sillage qui va être ressenti par les particules de queue du paquet et induire des
instabilités. Au bout d’une demi-période synchrotron, les particules de tête deviennent les particules
de queue et réciproquement. Ce type d’instabilité, dite head-tail, peut conduire à la
perte du faisceau. Il peut être montré (voir par exemple Lee, 1998) que ces instabilités
disparaissent à chromaticités nulles et sont plus néfastes pour des chromaticités négatives que
positives.
Dans un anneau de stockage, la chromaticité doit être soit nulle soit légèrement
positive. Pour la compenser, on introduit dans l’anneau des éléments nonlinéaires : les
hexapôles.
1.3.2 Dynamique nonlinéaire
Le Hamiltonien complet 1.36 peut maintenant être écrit sous la forme :
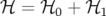 | (1.75) |
où 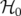 décrit le mouvement linéaire d’une machine parfaite (cf. Eq. 1.54) et
décrit le mouvement linéaire d’une machine parfaite (cf. Eq. 1.54) et 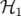 contient les
défauts de champs dipolaires, quadripolaires et le potentiel vecteur des multipôles. Si
contient les
défauts de champs dipolaires, quadripolaires et le potentiel vecteur des multipôles. Si 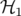 est
suffisamment faible, le mouvement va être encore stable. Toutes les grandeurs linéaires définies
précédemment ne vont plus être des constantes du mouvement.
est
suffisamment faible, le mouvement va être encore stable. Toutes les grandeurs linéaires définies
précédemment ne vont plus être des constantes du mouvement.
En particulier, les nombres d’ondes vont varier avec l’amplitude et l’énergie et peuvent au
premier ordre d’une théorie des perturbations s’écrire (voir par exemple Guignard, 1978, Ruth et
al., 1985 ou Wiedemann, 1995) :
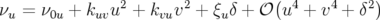 | (1.76) |
avec si  ,
,  et vice versa. La contribution linéaire définit le point de fonctionnement de
la machine (
et vice versa. La contribution linéaire définit le point de fonctionnement de
la machine (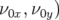 . Les coefficients
. Les coefficients 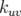 et
et 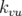 sont les premiers termes introduits par les
nonlinéarités.
sont les premiers termes introduits par les
nonlinéarités.
La principale cause de nonlinéarité dans un accélérateur d’électrons provient de l’introduction
des hexapôles. Regardons succinctement les effets qu’ils induisent. Pour cela, décrivons brièvement
le principe de correction de la chromaticité : lorsqu’un hexapôle n’est pas traversé en son centre,
une composante quadripolaire apparaît et peut être judicieusement utilisée pour corriger la
chromaticité. Les équations du mouvement pour un hexapôle de force  s’écrivent (cf.
Eq. 1.53 et Eq. 1.54) :
s’écrivent (cf.
Eq. 1.53 et Eq. 1.54) :
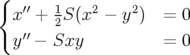 | (1.77) |
Pour un hexapôle de longueur infinitésimale 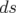 , on a alors :
, on a alors :
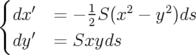 | (1.78) |
Pour la correction chromatique, il est nécessaire de pouvoir distinguer les trajectoires
correspondant aux différentes énergies : on se place donc dans une région
dispersive.
En utilisant les équations 1.72 et 1.78, il advient :
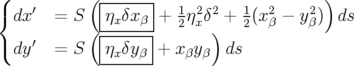 | (1.79) |
Il peut être démontré simplement qu’un défaut de gradient intégré 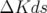 localisé en
localisé en  introduit le glissement des nombres d’ondes (voir par exemple Lee, 1998) :
introduit le glissement des nombres d’ondes (voir par exemple Lee, 1998) :
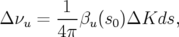 | (1.80) |
formule qui se généralise pour une distribution de défauts 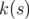 à l’intégrale sur la circonférence de
l’accélérateur :
à l’intégrale sur la circonférence de
l’accélérateur :
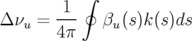 | (1.81) |
Si l’on ne considère que la partie quadripolaire de l’équation 1.79, le défaut local de
focalisation  apparaît. En utilisant alors la définition de la chromaticité 1.74 et
l’équation 1.81, on déduit immédiatement que la participation à la chromaticité des hexapôles
s’écrit :
apparaît. En utilisant alors la définition de la chromaticité 1.74 et
l’équation 1.81, on déduit immédiatement que la participation à la chromaticité des hexapôles
s’écrit :
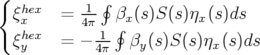 | (1.82) |
En principe, deux familles hexapolaires de force intégrée 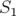 et
et 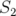 suffisent pour compenser les
deux chromaticités ; les forces doivent alors satisfaire pour chaque maille d’une machine
N-périodique :
suffisent pour compenser les
deux chromaticités ; les forces doivent alors satisfaire pour chaque maille d’une machine
N-périodique :
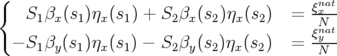 | (1.83) |
en supposant que les deux hexapôles sont localisés respectivement en  et
et  .
.
Les hexapôles (parfaits) introduisent deux sortes d’effets indésirables (cf. Eq. 1.79) :
- un terme d’aberration chromatique
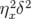
- deux termes d’aberration géométrique
 et
et 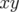
Ces termes d’aberration sont généralement corrigés partiellement en introduisant de nouvelles familles
d’hexapôles dans la maille de la machine.
Dans un accélérateur circulaire, la deuxième contribution aux nonlinéarités provient
des défauts magnétiques des aimants (déplacements, rotations d’un élément, champs
de fuite, composantes multipolaires). Ces défauts sont systématiques ou aléatoires et
inhérents à l’accélérateur. Nous verrons au cours des chapitres suivants qu’une bonne
connaissance des défauts quadripolaires permet déjà de bien modéliser la dynamique de
l’accélérateur.
Les défauts magnétiques induisent des phénomènes résonants qui détériorent la stabilité et les
performances de la machine.
1.4 Définitions complémentaires
1.4.1 Résonances
La dynamique transverse est modélisée par un système à (2+1) degrés de liberté. La
condition de résonance est obtenue pour une combinaison linéaire entre les nombres
d’ondes transverses  ,
, 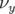 et le nombre d’ondes longitudinale normalisé à
et le nombre d’ondes longitudinale normalisé à  ,
i.e. :
,
i.e. :
 | (1.84) |
Habituellement  est appelé l’ordre de la résonance et correspond à l’ordre des polynômes
du développement du potentiel vecteur. Cependant, il est souvent plus judicieux de définir l’ordre
par l’entier
est appelé l’ordre de la résonance et correspond à l’ordre des polynômes
du développement du potentiel vecteur. Cependant, il est souvent plus judicieux de définir l’ordre
par l’entier 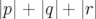 à partir de l’équation :
à partir de l’équation :
![3
p[νx] + q[νy] + r = 0 avec (p,q,r) ∈ ℤ](these393x.png) | (1.85) |
où ![[]](these394x.png) désigne la partie fractionnaire des nombres d’ondes. Cette définition, plus naturelle,
correspond à celle adoptée en Mécanique Céleste. Dans la suite, l’ordre des résonances défini avec
cette convention sera noté par
désigne la partie fractionnaire des nombres d’ondes. Cette définition, plus naturelle,
correspond à celle adoptée en Mécanique Céleste. Dans la suite, l’ordre des résonances défini avec
cette convention sera noté par  .
.
Pour une machine N-périodique, i.e. constituée de  super-périodes, la condition de
résonance est plus stricte : la dynamique de la machine totale est alors la même que pour une seule
super-période avec pour fréquence longitudinale
super-périodes, la condition de
résonance est plus stricte : la dynamique de la machine totale est alors la même que pour une seule
super-période avec pour fréquence longitudinale  .
.
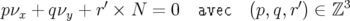 | (1.86) |
Plus un accélérateur a une périodicité élevée, plus la condition de résonance est sévère (cf.
Fig. 1.6). Dans la suite, nous parlerons de résonances permises, systématiques ou de structure et de
résonances interdites, sous-entendu par la périodicité.
Dans une théorie de perturbation simplement résonante du premier ordre, il peut être montré
que, pour des résonances sommes (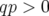 ), la différence des émittances
), la différence des émittances  est conservée.
Pour des résonances différences (
est conservée.
Pour des résonances différences (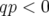 ), c’est la somme des émittances
), c’est la somme des émittances  qui est conservée
(voir par exemple : A General Treatment of Resonances in Accelerators, Guignard, 1978).
Dans le premier cas, il peut y avoir amplification mutuelle des amplitudes d’oscillation
(proportionnelles à la racine carrée de l’émittance), ce qui conduira à la divergence des
trajectoires des particules alors que pour des résonances différences, il ne peut y avoir que
transfert d’amplitudes d’oscillation entre les deux plans. Durant ma thèse, j’ai parfois
entendu dire que les résonances différences ne sont pas dangereuses pour la dynamique du
faisceau. En conséquence, les largeurs des résonances différences ne sont pas toujours
optimisées. Il est clair que ce résultat est celui d’une théorie de perturbation du premier
ordre et qu’il n’est valide qu’au voisinage d’une résonance unique. Proche d’un nœud de
résonances, les largeurs de résonances peuvent se recouvrir et la dynamique est toute
autre.
qui est conservée
(voir par exemple : A General Treatment of Resonances in Accelerators, Guignard, 1978).
Dans le premier cas, il peut y avoir amplification mutuelle des amplitudes d’oscillation
(proportionnelles à la racine carrée de l’émittance), ce qui conduira à la divergence des
trajectoires des particules alors que pour des résonances différences, il ne peut y avoir que
transfert d’amplitudes d’oscillation entre les deux plans. Durant ma thèse, j’ai parfois
entendu dire que les résonances différences ne sont pas dangereuses pour la dynamique du
faisceau. En conséquence, les largeurs des résonances différences ne sont pas toujours
optimisées. Il est clair que ce résultat est celui d’une théorie de perturbation du premier
ordre et qu’il n’est valide qu’au voisinage d’une résonance unique. Proche d’un nœud de
résonances, les largeurs de résonances peuvent se recouvrir et la dynamique est toute
autre.
1.4.2 Acceptances et ouvertures
1.4.2.1 Définitions
L’acceptance physique est par définition l’aire de la plus grande ellipse que l’accélérateur accepte
(cf. Eq. 1.72) :
![[ 2]
A = π au(s) −-|ηu(s)δ| avec u = x,y
u βu(s) min](these403x.png) | (1.87) |
et 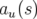 , la demi-ouverture physique et
, la demi-ouverture physique et  la dispersion locale.
la dispersion locale.
L’acceptance dynamique est définie comme la plus grande région de l’espace des phases
(dimension 6) à l’intérieur de laquelle les trajectoires de particules sont bornées, ceci en ne
considérant que la dynamique d’une particule isolée. Restreinte à l’espace transverse, on parle
d’ouverture dynamique, restreinte à la dynamique longitudinale, d’acceptance en énergie ou
RF.
La détermination des dimensions de l’ouverture dynamique est fondamentale mais non triviale.
Sa définition dépend du nombre de tours d’intégration des orbites. Par exemple Irwin (in Chao et
Tigner, pp. 87–91) donne comme nombre de tours optimum, vingt-cinq pour cent du temps
d’amortissement du faisceau, soit environ 1 000 tours pour des électrons. Cette limite est cependant
trop faible pour étudier finement la dynamique à long terme (estimation de la diffusion,
coefficients de Lyapunov), car les trajectoires des particules peuvent diverger aussi bien
au bout d’un très faible nombre de tours (diffusion rapide) que lentement (diffusion
d’Arnold) comme nous le verrons plus tard. La définition de l’ouverture dynamique dépend
aussi des phases auxquelles elle est tracée (généralement 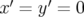 ), car les orbites se
déforment.
), car les orbites se
déforment.
Un problème ouvert est actuellement la recherche d’un facteur de qualité pour l’optimisation de
l’ouverture dynamique (voir Todesco, 1999).
1.4.2.2 Un schéma d’optimisation de l’ouverture dynamique
De par les nonlinéarités, il n’existe pas de méthode analytique générale pour optimiser l’ouverture
dynamique. Je présente ici le processus empirique d’optimisation d’une maille utilisé pour le Projet
SOLEIL (Nghiem et al., 1997) ; c’est un processus en quatre étapes :
La première étape consiste à choisir un point de fonctionnement dans une région du diagramme
des nombres d’ondes (cf. Fig. 1.6) où non seulement, une émittance faible peut être
obtenue mais aussi où il y a un minimum de résonances systématiques. Il est en particulier
primordial d’éviter la proximité (a) des résonances d’ordres entiers qui sont excitées par les
erreurs d’orbite fermée ; (b) des résonances d’ordres demi-entiers qui sont excitées par les
erreurs de gradients quadripolaires ; (c) des résonances sommes pour éviter l’amplification
mutuelle des oscillations bétatrons horizontales et verticales ; (d) des résonances du
troisième ordre qui sont introduites par les hexapôles. Ces critères permettent d’obtenir
une ouverture dynamique peu sensible aux défauts magnétiques et à l’introduction des
insertions.
La deuxième étape concerne l’optimisation des fonctions
bétatrons :
(a) la fonction 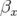 doit être minimum dans les dipôles pour obtenir une faible émittance ; (b) la
création de hautes brillances issues des insertions contraint la fonction
doit être minimum dans les dipôles pour obtenir une faible émittance ; (b) la
création de hautes brillances issues des insertions contraint la fonction 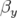 ; (c) le rapport
; (c) le rapport
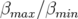 doit être minimum pour l’injection du faisceau ; de plus les fonctions bétatrons ne
doivent pas être trop grandes pour éviter d’avoir une sensibilité trop importante aux
erreurs magnétiques. Il est également souhaitable de conserver la symétrie la plus élevée
possible.
doit être minimum pour l’injection du faisceau ; de plus les fonctions bétatrons ne
doivent pas être trop grandes pour éviter d’avoir une sensibilité trop importante aux
erreurs magnétiques. Il est également souhaitable de conserver la symétrie la plus élevée
possible.
La troisième étape est le positionnement des hexapôles dans la maille. Les forces hexapolaires
doivent être les plus faibles possibles, car elles limitent l’ouverture dynamique. Les hexapôles sont
placés dans les régions à grande dispersion où les fonctions 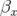 et
et  sont découplées
(Eq. 1.79).
sont découplées
(Eq. 1.79).
La quatrième et dernière étape est dédiée à la correction de la chromaticité et l’optimisation de
l’ouverture dynamique proprement dit. Seule l’ouverture dynamique on momentum ( ) est
optimisée. La minimisation des résonances hexapolaires d’ordre 3 est fondée sur une méthode
analytique du premier ordre (voir la thèse de Audy, 1989).
) est
optimisée. La minimisation des résonances hexapolaires d’ordre 3 est fondée sur une méthode
analytique du premier ordre (voir la thèse de Audy, 1989).
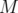 dipôles courbe la trajectoire du
faisceau d’un angle
dipôles courbe la trajectoire du
faisceau d’un angle 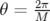 . Des quadripôles sont utilisés comme lentilles magnétiques pour
focaliser les particules. Ces deux principaux types d’éléments ainsi que la section droite
(absence de champ électromagnétique) définissent l’optique linéaire de l’anneau, en
référence à l’approximation paraxiale utilisée. L’agencement de ces éléments définit
la maille de l’accélérateur. Si l’anneau de stockage est constitué de
. Des quadripôles sont utilisés comme lentilles magnétiques pour
focaliser les particules. Ces deux principaux types d’éléments ainsi que la section droite
(absence de champ électromagnétique) définissent l’optique linéaire de l’anneau, en
référence à l’approximation paraxiale utilisée. L’agencement de ces éléments définit
la maille de l’accélérateur. Si l’anneau de stockage est constitué de  secteurs
identiques appelés super-périodes, alors il possède une symétrie interne qui permet
d’augmenter la stabilité globale de la dynamique (ce point sera abordé dans la
section 1.4).
secteurs
identiques appelés super-périodes, alors il possède une symétrie interne qui permet
d’augmenter la stabilité globale de la dynamique (ce point sera abordé dans la
section 1.4).
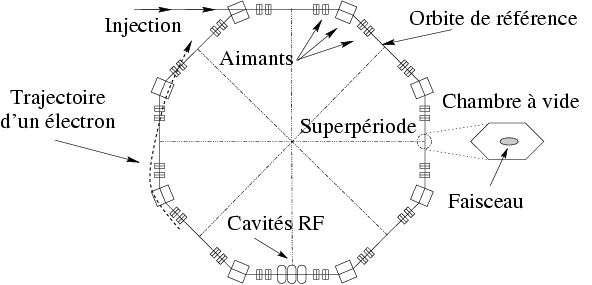
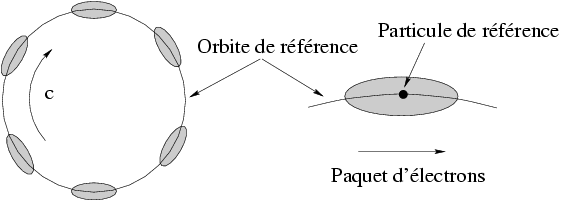
 , autour de l’orbite de référence. Au sein de chaque paquet, les particules
oscillent en longitude et en énergie (dynamique longitudinale) — inspiré de Sands, 1970
—
, autour de l’orbite de référence. Au sein de chaque paquet, les particules
oscillent en longitude et en énergie (dynamique longitudinale) — inspiré de Sands, 1970
— 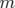 , puis nous plongerons la particule de charge
, puis nous plongerons la particule de charge  dans
un champ électromagnétique (section
dans
un champ électromagnétique (section  l’
l’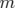 sa masse,
sa masse, 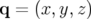 son
vecteur position et
son
vecteur position et  son vecteur vitesse. Par application du principe de relativité,
l’action doit être indépendante du choix du référentiel d’inertie, soit un invariant de
Lorentz
son vecteur vitesse. Par application du principe de relativité,
l’action doit être indépendante du choix du référentiel d’inertie, soit un invariant de
Lorentz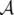 est donc un scalaire. De plus, il ne doit figurer que des
différentielles du premier degré sous le signe d’intégration (cf. Landau et Lifchitz,
est donc un scalaire. De plus, il ne doit figurer que des
différentielles du premier degré sous le signe d’intégration (cf. Landau et Lifchitz, 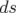 à une constante de proportionnalité près, notée
à une constante de proportionnalité près, notée
 .
.
 et
et 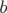 qui
sont les positions initiale et finale de la particule aux instants respectifs
qui
sont les positions initiale et finale de la particule aux instants respectifs 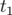 et
et 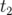 , alors l’action
, alors l’action 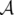 s’écrit
s’écrit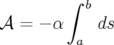
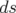 est donné par la métrique de Minkowski
est donné par la métrique de Minkowski
 est la vitesse de la lumière
est la vitesse de la lumière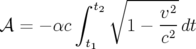
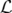 ), l’action est également définie par la relation (cf. Landau et
Lifchitz,
), l’action est également définie par la relation (cf. Landau et
Lifchitz, 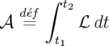
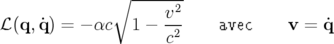
 est déterminée en passant à la limite
est déterminée en passant à la limite  qui doit redonner l’énergie
cinétique classique pour une particule libre
qui doit redonner l’énergie
cinétique classique pour une particule libre![1 v2 v4 1
ℒ (q,q˙) −−−−→ ℒclassique ⇐ ⇒ − αc + --α---+ 𝒪 (-3-) = [− mc2 ] +-mv2
c→+ ∞ 2 c c 2](these37x.png)
 . Le terme entre crochets est constant donc il n’intervient pas dans les équations du
mouvement
. Le terme entre crochets est constant donc il n’intervient pas dans les équations du
mouvement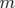 s’exprime finalement
par
s’exprime finalement
par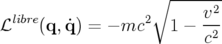

 ) caractérisant l’interaction de la
particule avec le champ électromagnétique
) caractérisant l’interaction de la
particule avec le champ électromagnétique 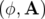 (voir Landau et Lifchitz,
(voir Landau et Lifchitz, 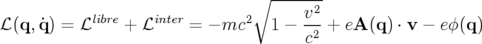
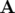 le potentiel vecteur et
le potentiel vecteur et 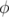 le potentiel scalaire solutions des équations de Maxwell.
le potentiel scalaire solutions des équations de Maxwell.
 s’obtiennent à partir du Lagrangien
s’obtiennent à partir du Lagrangien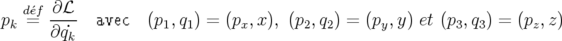
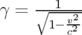

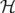 est obtenu à partir de la fonction de Lagrange
est obtenu à partir de la fonction de Lagrange 
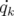

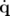

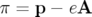 , on établit à partir des équations 1.10 et 1.11
la relation
, on établit à partir des équations 1.10 et 1.11
la relation


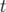
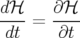
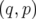 sont appelées
sont appelées  , sont définies par rapport au repère de
Serret-Frenet direct
, sont définies par rapport au repère de
Serret-Frenet direct 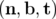
 et
et  est repérée par son vecteur position
est repérée par son vecteur position  par rapport à l’orbite de référence
par rapport à l’orbite de référence 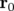 (voir
Fig.
(voir
Fig. 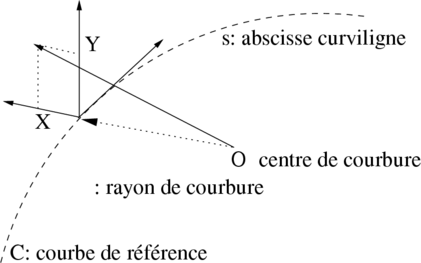

 . Définition des coordonnées curvilignes
. Définition des coordonnées curvilignes
 utilisées pour écrire les équations du mouvement d’une particule autour de la
trajectoire de référence.
utilisées pour écrire les équations du mouvement d’une particule autour de la
trajectoire de référence.  sont respectivement les vecteurs tangent, normal et binormal
définis par
sont respectivement les vecteurs tangent, normal et binormal
définis par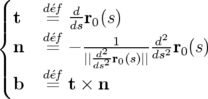
 et
et  décrivent la courbure et la torsion locales de la trajectoire à la longitude
décrivent la courbure et la torsion locales de la trajectoire à la longitude

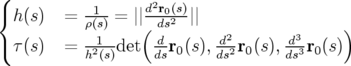
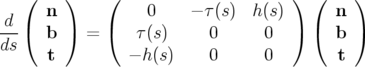
 et les nouvelles variables
et les nouvelles variables  .
Pour cela, on construit une fonction génératrice dépendant des anciens moments et des
nouvelles positions,
.
Pour cela, on construit une fonction génératrice dépendant des anciens moments et des
nouvelles positions, 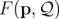 . Les changements de variables sont alors définis implicitement
par
. Les changements de variables sont alors définis implicitement
par
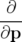

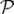

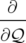
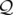

 est choisie nulle. L’équation
est choisie nulle. L’équation 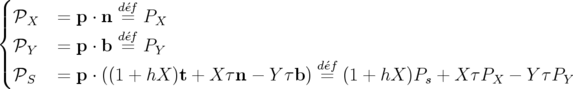
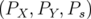 les projections usuelles de l’impulsion sur la base
les projections usuelles de l’impulsion sur la base 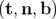 . On note également
que les coordonnées du potentiel vecteur
. On note également
que les coordonnées du potentiel vecteur 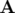 se transforment comme celles du moment
se transforment comme celles du moment  (cf.
équation
(cf.
équation  est nulle
est nulle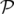

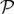
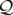
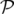


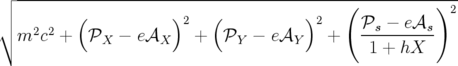
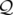
 (
( en
coordonnées rectangulaires ou
en
coordonnées rectangulaires ou  en coordonnées curvilignes).
en coordonnées curvilignes).
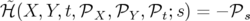 en notant
en notant 
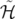
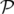
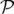
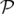


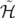 conjugue les couples de variables
conjugue les couples de variables 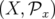 ,
, 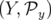 et
et
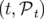
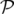


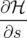
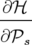


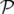
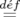

![[ ]
( ∂ℋ ) ( ∂ℋ ) −1 ( ∂ ℋ ) ( ∂ ℋ ) −1
----- ---- d𝒬k + ----- ---- d𝒫k
∂ 𝒬k ∂𝒫s ∂𝒫k ∂𝒫s](these134x.png)

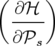

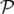
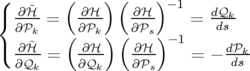 pour
pour 
 est physiquement reliée à la notion de temps de vol et son moment canonique
est physiquement reliée à la notion de temps de vol et son moment canonique 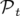 est
l’opposé de l’énergie totale de la particule. Pour la suite des calculs, on suppose que le potentiel électrique
est
l’opposé de l’énergie totale de la particule. Pour la suite des calculs, on suppose que le potentiel électrique
 est nul
est nul ,
on constate l’existence de la trajectoire particulière
,
on constate l’existence de la trajectoire particulière , que l’on
appelle
, que l’on
appelle 

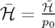 , soit
, soit
 . Le long de la trajectoire de référence, on a alors
. Le long de la trajectoire de référence, on a alors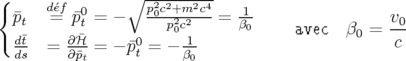
 (d’après Eq.
(d’après Eq. 
 . Si
. Si  est une fonction génératrice, le
nouveau Hamiltonien sera donné par
est une fonction génératrice, le
nouveau Hamiltonien sera donné par . Nous construisons la fonction génératrice
dépendant des anciennes positions et des nouveaux moments
. Nous construisons la fonction génératrice
dépendant des anciennes positions et des nouveaux moments 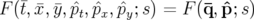 (Dragt et Forest, 1986)
(Dragt et Forest, 1986)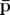
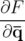

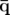

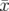
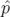
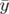
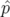
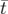
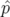

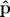
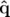
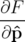

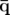
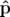

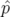
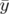


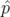

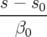

 est
est 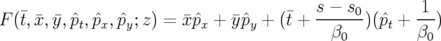


 .
.
 et
et  . Pour alléger l’écriture, les variables « perdent leur chapeau » (si
aucune confusion n’est possible) et on pose
. Pour alléger l’écriture, les variables « perdent leur chapeau » (si
aucune confusion n’est possible) et on pose  et
et 

 et
et 
 représente l’écart à énergie nominale
représente l’écart à énergie nominale  normalisée par l’énergie de la
particule nominale ultra-relativiste.
normalisée par l’énergie de la
particule nominale ultra-relativiste.
 est le temps de passage en
est le temps de passage en  de la particule synchrone. On suppose
que cette dernière se trouve en
de la particule synchrone. On suppose
que cette dernière se trouve en  en
en  . Si
. Si 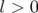 ,
, 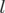 représente l’avance de la
particule par rapport à la particule synchrone.
représente l’avance de la
particule par rapport à la particule synchrone. qui ne dépend que des coordonnées transverses
qui ne dépend que des coordonnées transverses
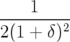


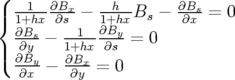
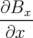
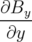
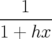
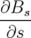
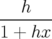
 vérifiant, à une
condition de jauge près
vérifiant, à une
condition de jauge près .
.
 est un plan d’antisymétrie pour le champ magnétique
(cf. symétrie des aimants, Fig.
est un plan d’antisymétrie pour le champ magnétique
(cf. symétrie des aimants, Fig. 
 ,
, 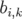 ,
, 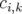 des fonctions de
des fonctions de  à déterminer.
à déterminer.
![( a′ = (i + 1)[c + hc ]
|||{ i,k i,k i− 1,k
ai,k = 2i+k1+1bi+1,k
| b′ = (2k + 1)[c + hc ]
||( i′,k i,k i−1,k
ci,k = − 2(k + 1)[bi,k+1 + hbi−1,k+1] − (i + 1)[ai+1,k + hai,k]](these227x.png)
 notée
notée  et par convention d’écriture un coefficient ayant un de ses
indices négatif est nul.
et par convention d’écriture un coefficient ayant un de ses
indices négatif est nul.
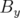 est mesuré en tant que fonction des coordonnées
est mesuré en tant que fonction des coordonnées 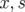 dans le plan
d’antisymétrie sous la forme
dans le plan
d’antisymétrie sous la forme
 (cf. Eq.
(cf. Eq. ![(
||Bx = B1,{0y + 2B2,0xy + 3B3,0x2y− }
|||| 1 hB1,0- B0′′,0 1 ′′ ′ ′ 3
||| 3 3B3,0 + 2hB2,0 − h(B2,0 + 2′′+ 2 ) + 2 [B 1,0 − (hB 0,0)] y + ...
|{By = B0,0 + B1,0x + B2,0x2 − (B2,0 + B0,0-+ hB1,0)y2 + B3,0x3−
{ hB1,02 B′′0,0 2 1 }
||| 3B3,0 + 2hB2,0 − h (B2,0 + --2--+ -2-) + 2[B ′1′,0 − (hB ′0,0)′] xy2 + ...
||| ′ ( ′ ′ ) ′ ′ 2 ′ 2
||||Bs = B 0,0(y + B1,0 −′hB 0,0′′′x)y + (B 2,0 − hB 1,0 + h B 0,0)x y
( − 13 B2′,0 + hB21,0+ B12,0- y3 + ...](these234x.png)
 (élément rectangulaire), le champ magnétique peut s’écrire à partir de
l’expression
(élément rectangulaire), le champ magnétique peut s’écrire à partir de
l’expression 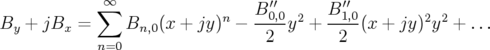
 .
.
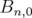 sont souvent pris constants, donc l’équation
sont souvent pris constants, donc l’équation 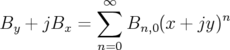
 avec
avec 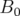 choisi tel que
choisi tel que  et avec
et avec
 où
où 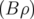 est la
est la 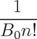
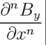
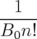
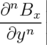
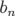 et
et 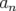 décrivent respectivement les
décrivent respectivement les 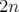 -pôles parfaits droits et
tournés.
-pôles parfaits droits et
tournés.
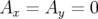 ) est lié au champ magnétique par l’équation,
) est lié au champ magnétique par l’équation,
 , soit exprimée en coordonnées curvilignes
, soit exprimée en coordonnées curvilignes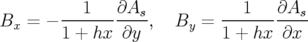
 ), la formule
), la formule 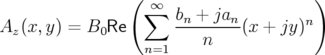
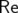 désigne la partie réelle. Deux types de représentations nous intéressent
désigne la partie réelle. Deux types de représentations nous intéressent ne peut pas
s’exprimer de manière aussi simple qu’en coordonnées rectangulaires (cf. Eq.
ne peut pas
s’exprimer de manière aussi simple qu’en coordonnées rectangulaires (cf. Eq. 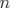 (voir par exemple la thèse
de Fartoukh, 1997). Cette description est adaptée aux éléments type dipôle de rayon de courbure
(voir par exemple la thèse
de Fartoukh, 1997). Cette description est adaptée aux éléments type dipôle de rayon de courbure
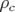 .
.
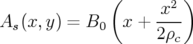
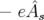 exprimée pour le Hamiltonien
exprimée pour le Hamiltonien 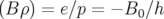 , on obtient
, on obtient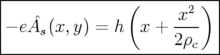
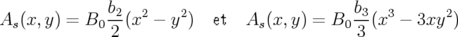
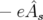
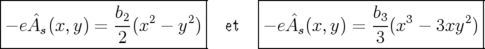
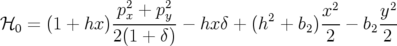

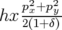 dans
l’expression du Hamiltonien
dans
l’expression du Hamiltonien  .
.
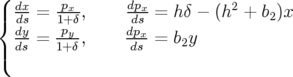
 et
et 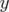 (en négligeant les
termes d’ordre 2 en
(en négligeant les
termes d’ordre 2 en 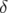 )
)
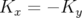 et
et 
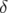 de la particule
de la particule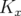 et
et 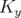 sont définies par morceaux à valeur constante dans chaque
élément magnétique et L-périodiques
sont définies par morceaux à valeur constante dans chaque
élément magnétique et L-périodiques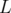
 et particule
et particule 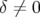 . Le symbole
. Le symbole  désigne la dérivation par rapport à la longitude
désigne la dérivation par rapport à la longitude  et
et  la
dérivée seconde.
la
dérivée seconde.
 comme l’équation
générique
comme l’équation
générique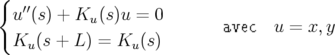
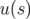 de l’équation de Hill
de l’équation de Hill  . Usuellement, la solution s’écrit de différentes
manières dans la littérature
. Usuellement, la solution s’écrit de différentes
manières dans la littérature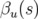
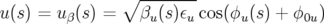
 ,
, 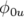 la phase à l’origine et
la phase à l’origine et 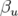 vérifiant l’équation
différentielle
vérifiant l’équation
différentielle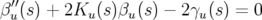
 et
et  . Les paramètres
. Les paramètres  ,
, 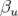 et
et 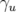 sont appelés
sont appelés 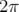 définit le
définit le 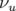
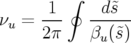

 dans le plan
dans le plan  (cf.
Fig.
(cf.
Fig. 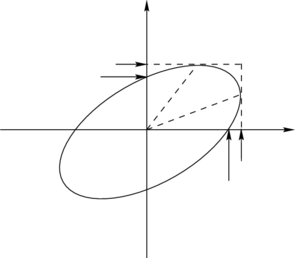

 ). L’aire de l’ellipse est
). L’aire de l’ellipse est 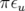
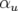 ,
, 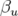 et
et 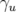 sont les fonctions de Twiss.
sont les fonctions de Twiss. 
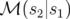 est la
est la 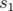 à
à 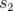 ,
,  l’avance de phase entre
l’avance de phase entre 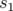 à
à 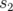 ,
, 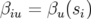 . Sur un tour complet, l’expression
. Sur un tour complet, l’expression 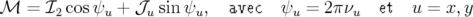
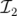 la matrice identité et
la matrice identité et
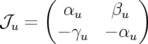
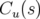 et
et 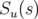 qui par définition sont deux solutions
indépendantes de l’équation de Hill
qui par définition sont deux solutions
indépendantes de l’équation de Hill 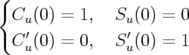
 peut alors s’écrire (Courant et Snyder,
1958)
peut alors s’écrire (Courant et Snyder,
1958)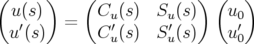
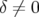 , l’équation
, l’équation 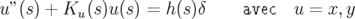
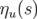 périodique pour
périodique pour
 de l’équation
de l’équation 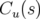 et
et  , la dispersion
linéaire est donnée par la formule (Lee, 1998)
, la dispersion
linéaire est donnée par la formule (Lee, 1998)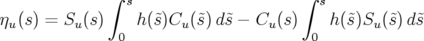

 la solution bétatron et
la solution bétatron et 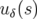 l’
l’ ). Si
). Si 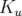 est le gradient quadripolaire, alors on peut
écrire (cf. Eq.
est le gradient quadripolaire, alors on peut
écrire (cf. Eq. 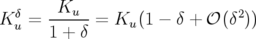
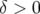 sont moins focalisées.
Il s’ensuit que l’avance de phase dans un élément quadripolaire devient une fonction de l’énergie, ce
qui nous conduit à définir la
sont moins focalisées.
Il s’ensuit que l’avance de phase dans un élément quadripolaire devient une fonction de l’énergie, ce
qui nous conduit à définir la 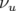 , en fonction
de l’énergie
, en fonction
de l’énergie
 . La contribution produite uniquement par les éléments linéaires,
. La contribution produite uniquement par les éléments linéaires,  et
et
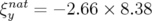 , ce qui induit pour
, ce qui induit pour  % les déplacements des nombres d’ondes proches
du demi-entier
% les déplacements des nombres d’ondes proches
du demi-entier  . Ces glissements des nombres d’ondes peuvent amener le
faisceau sur des lignes de résonance et conduire à des conséquences néfastes pour les performances
de l’anneau.
. Ces glissements des nombres d’ondes peuvent amener le
faisceau sur des lignes de résonance et conduire à des conséquences néfastes pour les performances
de l’anneau.
 décrit le mouvement linéaire d’une machine parfaite (cf. Eq.
décrit le mouvement linéaire d’une machine parfaite (cf. Eq.  contient les
défauts de champs dipolaires, quadripolaires et le potentiel vecteur des multipôles. Si
contient les
défauts de champs dipolaires, quadripolaires et le potentiel vecteur des multipôles. Si 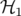 est
suffisamment faible, le mouvement va être encore stable. Toutes les grandeurs linéaires définies
précédemment ne vont plus être des constantes du mouvement.
est
suffisamment faible, le mouvement va être encore stable. Toutes les grandeurs linéaires définies
précédemment ne vont plus être des constantes du mouvement.
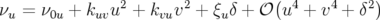
 ,
,  et
et 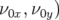 . Les coefficients
. Les coefficients 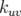 et
et 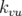 sont les premiers termes introduits par les
nonlinéarités.
sont les premiers termes introduits par les
nonlinéarités.
 s’écrivent (cf.
Eq.
s’écrivent (cf.
Eq. 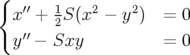
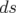 , on a alors
, on a alors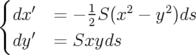
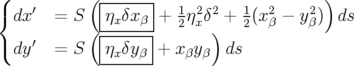
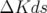 localisé en
localisé en  introduit le glissement des nombres d’ondes (voir par exemple Lee, 1998)
introduit le glissement des nombres d’ondes (voir par exemple Lee, 1998)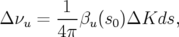
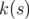 à l’intégrale sur la circonférence de
l’accélérateur
à l’intégrale sur la circonférence de
l’accélérateur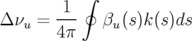
 apparaît. En utilisant alors la définition de la chromaticité
apparaît. En utilisant alors la définition de la chromaticité 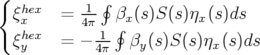
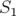 et
et 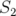 suffisent pour compenser les
deux chromaticités
suffisent pour compenser les
deux chromaticités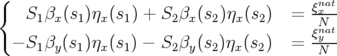
 et
et  .
.
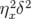
 et
et 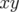
 ,
, 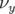 et le nombre d’ondes longitudinale normalisé à
et le nombre d’ondes longitudinale normalisé à  ,
,

 est appelé l’
est appelé l’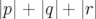 à partir de l’équation
à partir de l’équation![3
p[νx] + q[νy] + r = 0 avec (p,q,r) ∈ ℤ](these393x.png)
![[]](these394x.png) désigne la partie fractionnaire des nombres d’ondes. Cette définition, plus naturelle,
correspond à celle adoptée en Mécanique Céleste. Dans la suite, l’ordre des résonances défini avec
cette convention sera noté par
désigne la partie fractionnaire des nombres d’ondes. Cette définition, plus naturelle,
correspond à celle adoptée en Mécanique Céleste. Dans la suite, l’ordre des résonances défini avec
cette convention sera noté par  .
.
 super-périodes, la condition de
résonance est plus stricte
super-périodes, la condition de
résonance est plus stricte .
.
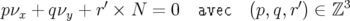

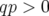 ), la différence des émittances
), la différence des émittances  est conservée.
Pour des
est conservée.
Pour des 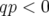 ), c’est la somme des émittances
), c’est la somme des émittances  qui est conservée
(voir par exemple
qui est conservée
(voir par exemple![[ 2]
A = π au(s) −-|ηu(s)δ| avec u = x,y
u βu(s) min](these403x.png)
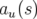 , la demi-
, la demi- la dispersion locale.
la dispersion locale.
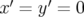 ), car les orbites se
déforment.
), car les orbites se
déforment.
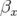 doit être minimum dans les dipôles pour obtenir une faible émittance
doit être minimum dans les dipôles pour obtenir une faible émittance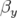
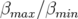 doit être minimum pour l’injection du faisceau
doit être minimum pour l’injection du faisceau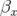 et
et  sont découplées
(Eq.
sont découplées
(Eq.  ) est
optimisée. La minimisation des résonances hexapolaires d’ordre 3 est fondée sur une méthode
analytique du premier ordre (voir la thèse de Audy, 1989).
) est
optimisée. La minimisation des résonances hexapolaires d’ordre 3 est fondée sur une méthode
analytique du premier ordre (voir la thèse de Audy, 1989).