4.6 Conclusions

Même si certaines expériences sur d’autres accélérateurs ont déjà utilisé l’association aimants rapides et de BPM tour par tour pour étudier la dynamique nonlinéaire (Lee, 1992) et si des tentatives pour relier l’Analyse en Fréquence et les mesures de fréquences ont été entreprises (Terebilo et al., 1998 — Bartolini et al., 1999) ; à notre connaissance, les résultats présentés sont les premiers de ce genre.

La réalisation de cartes en fréquence expérimentales à l’ALS montre le réseau complet de résonances d’un système hamiltonien à trois degrés de liberté. La comparaison entre les cartes en fréquence théoriques et mesurées démontre qu’un modèle relativement simple peut être utilisé pour caractériser correctement la dynamique du faisceau, i.e. en prenant en compte les forces nominales des hexapôles et les erreurs de gradients droits et tournés. Cet accord impressionnant nous permet d’utiliser dès maintenant de manière fiable l’Analyse en Fréquence comme outil standard pour faire de la prédiction de l’impact sur dynamique d’une modification de la maille de l’ALS. L’Analyse en Fréquence peut être utilisée pour optimiser nos simulations et pour valider notre modèle de l’anneau. La capacité de pouvoir calculer des cartes en fréquence indépendamment de tout modèle a été démontrée et l’interprétation de la diffusion sur les cartes en fréquence a été validée par les mesures de perte de faisceau sur les structures résonantes.

Toutes les simulations réalisées jusqu’ici ont été faites dans l’hypothèse que la dynamique de l’anneau de stockage est gouvernée principalement par la dynamique transverse faiblement perturbée par la dynamique longitudinale — négligée dans nos simulations puisque que le couplage synchro-bétatron est quasi-nul —. C’est bien ce qui a été observé sur les cartes en fréquence expérimentales. Au sujet de la diffusion des orbites, le phénomène est plus complexe que nous l’avons laissé entendre. La dynamique totale de l’accélérateur peut être décrite par un Hamiltonien à trois degrés de liberté dépendant de la longitude pris comme variable indépendante. L’espace des phases est de dimensions , l’application fréquence est alors une application de dans  :

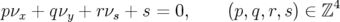Les cartes en fréquence que nous avons tracées dans tout ce manuscrit ne sont qu’une projection dans le plan 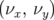. Ce qui signifie en particulier, que même dans une zone parfaitement régulière d’une carte en fréquence, il peut y avoir une diffusion due au degré de liberté longitudinal. Cependant, elle reste généralement très faible vis-à-vis de celles induites par la dynamique transverse.

Au cours de l’été 2001, la maille de l’ALS va connaître sa plus importante modification : trois des trente-six dipôles de la machine vont être remplacés par des aimants supraconducteurs. La périodicité de la machine va diminuer pour passer de 12 à 3. Pour une énergie nominale de 1.9 GeV, les fluctuations quantiques des aimants supra-conducteurs augmentent l’émittance horizontale de 5.5 à 13 nm.rad. Cette dernière peut être réduite en introduisant de la dispersion dans les sections droites. Le couplage (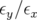) est néanmoins inférieur à 1%, et le temps de vie du faisceau n’est que d’environ deux heures (pour un courant de 1.3 mA par paquet). Pour retrouver un temps de vie acceptable, l’émittance verticale devra être augmentée en introduisant une dizaine de nouvelles familles de quadripôles tournés (cf. simulations de Nishimura et Robin, 1999). Nous comptons utiliser pleinement l’Analyse en Fréquence pour finir de comprendre l’influence de ses modifications — le but idéal serait d’arriver à les compenser entièrement — et de continuer d’améliorer les performances de l’ALS.