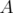 et
et 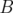 dans l’expression générale du Hamiltonien, les intégrateurs
symétriques peuvent appartenir à l’une des deux classes
dans l’expression générale du Hamiltonien, les intégrateurs
symétriques peuvent appartenir à l’une des deux classes 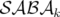 et
et 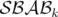 définies
par :
définies
par :
La classe d’intégrateurs que nous avons utilisée est présentée dans l’article de Laskar et Robutel (2000) auquel le lecteur pourra se référer pour plus de détails.
Si l’on distingue 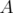 et
et 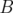 dans l’expression générale du Hamiltonien, les intégrateurs
symétriques peuvent appartenir à l’une des deux classes
dans l’expression générale du Hamiltonien, les intégrateurs
symétriques peuvent appartenir à l’une des deux classes 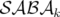 et
et 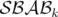 définies
par :
définies
par :
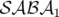 . C’est un intégrateur
d’ordre 2 avec pour Hamiltonien formel
. C’est un intégrateur
d’ordre 2 avec pour Hamiltonien formel 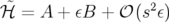 . L’intégrateur d’ordre 4 de Forest et
Ruth (Eq. 2.25) appartient à la classe
. L’intégrateur d’ordre 4 de Forest et
Ruth (Eq. 2.25) appartient à la classe 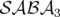 avec
avec 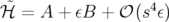 . Nous pouvons
remarquer la présence de deux pas négatifs pour cet intégrateur, ce qui rend la valeur absolue de
chaque pas intermédiaire relativement grande pour un pas total de 1 :
. Nous pouvons
remarquer la présence de deux pas négatifs pour cet intégrateur, ce qui rend la valeur absolue de
chaque pas intermédiaire relativement grande pour un pas total de 1 :  ,
,
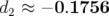 ,
, 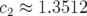 et
et  . Il s’ensuit que pour de grands pas d’intégration,
la méthode perd de son efficacité (coût élevé, instabilités numériques). Suzuki (1991) a
démontré qu’il est impossible de réaliser un intégrateur symplectique d’ordre
. Il s’ensuit que pour de grands pas d’intégration,
la méthode perd de son efficacité (coût élevé, instabilités numériques). Suzuki (1991) a
démontré qu’il est impossible de réaliser un intégrateur symplectique d’ordre 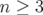 avec
des pas tous positifs. Cependant, le problème des pas négatifs peut être partiellement
solutionné.
avec
des pas tous positifs. Cependant, le problème des pas négatifs peut être partiellement
solutionné.
Jusqu’à présent, nous n’avons pas pris en compte l’existence du petit paramètre  . La méthode
retenue consiste à déterminer les coefficients
. La méthode
retenue consiste à déterminer les coefficients 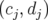 des intégrateurs 2.27 pour avoir un reste
d’ordre
des intégrateurs 2.27 pour avoir un reste
d’ordre 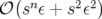 et non plus d’ordre
et non plus d’ordre 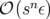 .
.
Par exemple pour un intégrateur de classe 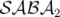 (ordre quatre), on a :
(ordre quatre), on a :
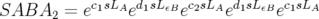 | (2.28) |
l’unique solution pour les coefficients est :
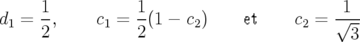 |
avec
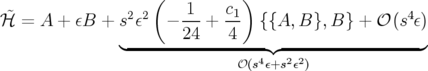 | (2.29) |
De manière similaire pour un intégrateur de classe 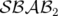 ,
,
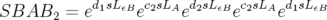 | (2.30) |
les coefficients positifs solutions sont l’unique triplet :
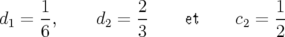 |
Ce sont ces deux intégrateurs qui ont été retenus pour l’écriture du code de tracking.
En fait, dans le cas particulier où 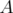 est quadratique en les impulsions et
est quadratique en les impulsions et 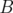 ne dépend que des
positions, il est possible d’améliorer encore la méthode en introduisant un correcteur
ne dépend que des
positions, il est possible d’améliorer encore la méthode en introduisant un correcteur 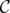 défini par
(voir Laskar et Robutel, 2000) :
défini par
(voir Laskar et Robutel, 2000) :
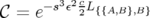 | (2.31) |
où le coefficient du correcteur  est déterminé pour annuler le terme d’ordre
est déterminé pour annuler le terme d’ordre 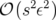 (voir par
exemple l’expression 2.29 pour l’intégrateur
(voir par
exemple l’expression 2.29 pour l’intégrateur 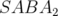 ). On notera que le correcteur introduit un
pas négatif, mais qu’il est d’autant plus petit que l’ordre de la méthode est élevé (Tab 2.2).
). On notera que le correcteur introduit un
pas négatif, mais qu’il est d’autant plus petit que l’ordre de la méthode est élevé (Tab 2.2).
|
|
Typiquement, le schéma symplectique avec correcteur s’écrit, par exemple pour un intégrateur
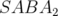 :
:
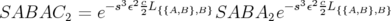 | (2.32) |
L’intégrateur avec correcteur est encore symétrique et son reste est d’ordre 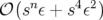 .
.
Les intégrateurs que j’utiliserai sont d’ordre deux et quatre. Typiquement, un intégrateur
d’ordre 4 sera utilisé pour intégrer les éléments de type dipôles, quadripôles alors qu’un intégrateur
d’ordre  suffira pour l’intégration des multipôles individuels.
suffira pour l’intégration des multipôles individuels.
Nous montrerons qu’un intégrateur d’ordre deux avec correcteur est plus précis d’un ordre de grandeur que l’intégrateur de Ruth (cf. infra). Je vais maintenant présenter le Hamiltonien local pour chacun des principaux éléments magnétiques et les approximations réalisées.