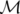 l’application de transfert et
l’application de transfert et  sa matrice jacobienne,
alors par définition la transformation est symplectique si et seulement si (Goldstein,
1980) :
sa matrice jacobienne,
alors par définition la transformation est symplectique si et seulement si (Goldstein,
1980) :
Pour effectuer cette étude, plusieurs logiciels pouvaient être utilisés13 :
Le programme DESPOT a dû être abandonné dès le début pour cette étude, car il ne modélise pas les champs de fuite d’un dipôle : tout le code est écrit dans l’approximation des grandes machines.
Le programme BETA a l’inconvénient d’être lourdement interfacé et interactif, rendant son utilisation difficile pour des calculs longs tels ceux d’une carte en fréquence. Cependant étant utilisé au LURE, dans un premier temps, il n’a pas été écarté.
L’ensemble de la discussion va porter sur une description de Super-ACO sans défaut, i.e. pour une machine idéale.
Lorsque les champs de fuite sont inclus dans le modèle de la dynamique, les calculs
effectués avec le code BETA à l’ordre 2 ne sont plus symplectiques. En fait, leur inclusion
dans le développement de Taylor d’ordre 2 « tue » la symplecticité de l’intégrateur (cf.
Fig. 3.15). Si l’on appelle 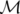 l’application de transfert et
l’application de transfert et  sa matrice jacobienne,
alors par définition la transformation est symplectique si et seulement si (Goldstein,
1980) :
sa matrice jacobienne,
alors par définition la transformation est symplectique si et seulement si (Goldstein,
1980) :
 |
avec 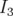 et
et 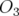 respectivement les matrices identité et nulle de rang 3. Ces conditions de
symplecticité se traduisent par 15 relations pour un système à 3 degrés de liberté. Dans le logiciel
BETA, la matrice de transfert prend en compte les termes du second ordre. Ainsi programmé, le
nombre de relations de symplecticité est plus élevé (quelques conditions devant être théoriquement
nulles, si le schéma d’intégration est symplectique, sont données par le tableau 3.4). Il ne
faut donc pas utiliser BETA au second ordre pour Super-ACO mais utiliser l’ordre dit
scaling14
qui prend correctement en compte les champs de fuite.
respectivement les matrices identité et nulle de rang 3. Ces conditions de
symplecticité se traduisent par 15 relations pour un système à 3 degrés de liberté. Dans le logiciel
BETA, la matrice de transfert prend en compte les termes du second ordre. Ainsi programmé, le
nombre de relations de symplecticité est plus élevé (quelques conditions devant être théoriquement
nulles, si le schéma d’intégration est symplectique, sont données par le tableau 3.4). Il ne
faut donc pas utiliser BETA au second ordre pour Super-ACO mais utiliser l’ordre dit
scaling14
qui prend correctement en compte les champs de fuite.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Si les champs de fuite des dipôles sont négligés, au second ordre, le système intégré reste
symplectique (comme on l’attend), mais uniquement à très faible amplitude (e.g.  mm).
Par contre dès
mm).
Par contre dès 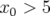 mm, l’espace des phases se peuple de trajectoires spirales caractéristiques
ici encore de la non-symplecticité. Après quelques discussions fructueuses avec J. Payet, il s’avère
que la seconde raison de non-symplecticité est le faible rayon de courbure de Super-ACO,
mm, l’espace des phases se peuple de trajectoires spirales caractéristiques
ici encore de la non-symplecticité. Après quelques discussions fructueuses avec J. Payet, il s’avère
que la seconde raison de non-symplecticité est le faible rayon de courbure de Super-ACO,
 m. Notons cependant que ce problème est général pour pratiquement tous les logiciels de
tracking — second ordre de MAD compris — car l’approximation des grands rayons de courbure,
abusivement utilisée, est souvent oubliée.
m. Notons cependant que ce problème est général pour pratiquement tous les logiciels de
tracking — second ordre de MAD compris — car l’approximation des grands rayons de courbure,
abusivement utilisée, est souvent oubliée.
La conclusion est l’obligation d’utiliser le code BETA à l’ordre scaling pour tous les calculs de Super-ACO.
Une fois ces premiers problèmes cernés, une comparaison des résultats obtenus avec les logiciels BETA et MAD a été réalisée. Rappelons que parmi les critères recherchés, la rapidité de calcul et la validité du code à grandes amplitudes sur un grand nombre de tours sont primordiales pour utiliser l’Analyse en Fréquence.
La figure 3.16 illustre un bogue lors du calcul de la contribution des multipôles dans BETA. Alors qu’à l’ordre scaling, les résultats devraient être strictement identiques en mode15 XZ ou QXZ, ils sont totalement dissemblables, en particulier pour la variation du nombre d’ondes horizontal avec l’amplitude. Après discussion avec J. Payet, il s’avère que les calculs doivent être réalisés en mode XZ (plus lent que le mode QXZ mais « moins imprécis » !).
|
|
Ajoutons enfin, que l’ordre scaling est une approximation qui est valide seulement à faible
amplitude. En comparant les résultats entre BETA et MAD, il s’avère que les résultats diffèrent dès
 mm16,
amplitude relativement faible puisque l’acceptance physique de la machine est
mm16,
amplitude relativement faible puisque l’acceptance physique de la machine est  mm !
Au-delà, les résultats de BETA sont complètement faux, car les approximations de calcul ne sont
plus vérifiées.
mm !
Au-delà, les résultats de BETA sont complètement faux, car les approximations de calcul ne sont
plus vérifiées.
Dans la suite, sauf cas explicitement dit, je n’utilise plus que l’intégrateur LIE4 de MAD qui est assez lent mais « exact » à grande amplitude car symplectique d’ordre quatre.
Pour finir, remarquons qu’on n’observe pas de différence notable pour le calcul de  avec BETA mode QXZ, XZ ou LIE4 de MAD. Ce résultat se comprend immédiatement, car les
lentilles décapolaires induisent le champ magnétique suivant :
avec BETA mode QXZ, XZ ou LIE4 de MAD. Ce résultat se comprend immédiatement, car les
lentilles décapolaires induisent le champ magnétique suivant :
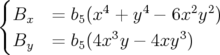 | (3.1) |
où 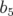 est la force octupolaire (cf. l’expression générale 1.46 du champ magnétique, p. §). Or les
calculs précédents ont été réalisés pour
est la force octupolaire (cf. l’expression générale 1.46 du champ magnétique, p. §). Or les
calculs précédents ont été réalisés pour  ou
ou  (couplage non pris en compte dans ce
type de calcul par le code BETA) ; les champs magnétiques se simplifient dans le premier cas à
(couplage non pris en compte dans ce
type de calcul par le code BETA) ; les champs magnétiques se simplifient dans le premier cas à
 et dans le second cas à
et dans le second cas à  . Donc, il n’y a pas d’influence
notable dans le plan vertical.
. Donc, il n’y a pas d’influence
notable dans le plan vertical.
Malgré ses qualités, le code BETA n’est pas adapté pour effectuer de longues intégrations numériques et des optimisations à grandes amplitudes (pour une machine à faible rayon de courbure). D’ailleurs, il n’a pas été écrit dans cette optique (cf. les approximations réalisées).