1.2.1 Lagrangien relativiste
Soit  l’intégrale d’action pour une particule libre relativiste,
l’intégrale d’action pour une particule libre relativiste, 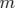 sa masse,
sa masse, 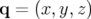 son
vecteur position et
son
vecteur position et  son vecteur vitesse. Par application du principe de relativité,
l’action doit être indépendante du choix du référentiel d’inertie, soit un invariant de
Lorentz : l’intégrale d’action
son vecteur vitesse. Par application du principe de relativité,
l’action doit être indépendante du choix du référentiel d’inertie, soit un invariant de
Lorentz : l’intégrale d’action  est donc un scalaire. De plus, il ne doit figurer que des
différentielles du premier degré sous le signe d’intégration (cf. Landau et Lifchitz, Physique
théorique : Théorie des Champs, chap. I et II). La seule solution pour une particule
libre est alors l’intervalle relativiste
est donc un scalaire. De plus, il ne doit figurer que des
différentielles du premier degré sous le signe d’intégration (cf. Landau et Lifchitz, Physique
théorique : Théorie des Champs, chap. I et II). La seule solution pour une particule
libre est alors l’intervalle relativiste  à une constante de proportionnalité près, notée
à une constante de proportionnalité près, notée
 .
.
Si l’intégrale est prise sur une ligne d’univers s’étendant entre deux événements  et
et 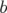 qui
sont les positions initiale et finale de la particule aux instants respectifs
qui
sont les positions initiale et finale de la particule aux instants respectifs 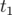 et
et 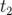 , alors l’action
, alors l’action 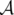 s’écrit :
s’écrit :
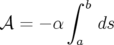 | (1.1) |
Or l’intervalle relativiste 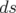 est donné par la métrique de Minkowski :
est donné par la métrique de Minkowski :
 | (1.2) |
où  est la vitesse de la lumière ; donc l’action 1.1 peut se réécrire :
est la vitesse de la lumière ; donc l’action 1.1 peut se réécrire :
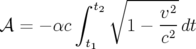 | (1.3) |
Par définition du Lagrangien (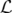 ), l’action est également définie par la relation (cf. Landau et
Lifchitz, Physique théorique : Mécanique, chap. I) :
), l’action est également définie par la relation (cf. Landau et
Lifchitz, Physique théorique : Mécanique, chap. I) :
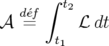 | (1.4) |
On déduit des équations 1.3 et 1.4 l’expression du Lagrangien :
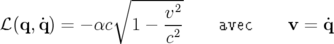 | (1.5) |
La constante  est déterminée en passant à la limite
est déterminée en passant à la limite  qui doit redonner l’énergie
cinétique classique pour une particule libre ; en effectuant un développement limité à l’ordre un de
l’expression 1.5, on obtient :
qui doit redonner l’énergie
cinétique classique pour une particule libre ; en effectuant un développement limité à l’ordre un de
l’expression 1.5, on obtient :
![classique 1 v2 v4 2 1 2
ℒ (q,q˙) −−−−→ ℒ ⇐ ⇒ − αc + --α---+ 𝒪 (-3-) = [− mc ] +--mv
c→+ ∞ 2 c c 2](these37x.png) | (1.6) |
d’où  . Le terme entre crochets est constant donc il n’intervient pas dans les équations du
mouvement : il correspond à l’énergie de masse de la particule.
. Le terme entre crochets est constant donc il n’intervient pas dans les équations du
mouvement : il correspond à l’énergie de masse de la particule.
Le Lagrangien d’une particule libre relativiste de masse 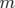 s’exprime finalement
par :
s’exprime finalement
par :
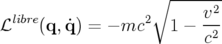 | (1.7) |
Pour une particule relativiste de charge  en mouvement dans un champ électromagnétique, le
Lagrangien total comporte un terme supplémentaire (
en mouvement dans un champ électromagnétique, le
Lagrangien total comporte un terme supplémentaire ( ) caractérisant l’interaction de la
particule avec le champ électromagnétique
) caractérisant l’interaction de la
particule avec le champ électromagnétique 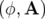 (voir Landau et Lifchitz, Théorie des Champs,
chap. III) :
(voir Landau et Lifchitz, Théorie des Champs,
chap. III) :
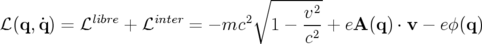 | (1.8) |
avec 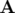 le potentiel vecteur et
le potentiel vecteur et 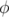 le potentiel scalaire solutions des équations de Maxwell.
le potentiel scalaire solutions des équations de Maxwell.
 l’intégrale d’action pour une particule libre relativiste,
l’intégrale d’action pour une particule libre relativiste, 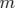 sa masse,
sa masse, 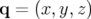 son
vecteur position et
son
vecteur position et  son vecteur vitesse. Par application du principe de relativité,
l’action doit être indépendante du choix du référentiel d’inertie, soit un invariant de
Lorentz : l’intégrale d’action
son vecteur vitesse. Par application du principe de relativité,
l’action doit être indépendante du choix du référentiel d’inertie, soit un invariant de
Lorentz : l’intégrale d’action 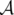 est donc un scalaire. De plus, il ne doit figurer que des
différentielles du premier degré sous le signe d’intégration (cf. Landau et Lifchitz, Physique
théorique : Théorie des Champs, chap. I et II). La seule solution pour une particule
libre est alors l’intervalle relativiste
est donc un scalaire. De plus, il ne doit figurer que des
différentielles du premier degré sous le signe d’intégration (cf. Landau et Lifchitz, Physique
théorique : Théorie des Champs, chap. I et II). La seule solution pour une particule
libre est alors l’intervalle relativiste 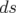 à une constante de proportionnalité près, notée
à une constante de proportionnalité près, notée
 .
.
 et
et 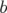 qui
sont les positions initiale et finale de la particule aux instants respectifs
qui
sont les positions initiale et finale de la particule aux instants respectifs 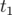 et
et 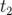 , alors l’action
, alors l’action 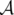 s’écrit
s’écrit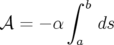
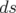 est donné par la métrique de Minkowski
est donné par la métrique de Minkowski
 est la vitesse de la lumière
est la vitesse de la lumière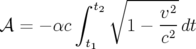
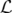 ), l’action est également définie par la relation (cf. Landau et
Lifchitz,
), l’action est également définie par la relation (cf. Landau et
Lifchitz, 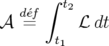
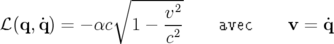
 est déterminée en passant à la limite
est déterminée en passant à la limite  qui doit redonner l’énergie
cinétique classique pour une particule libre
qui doit redonner l’énergie
cinétique classique pour une particule libre![classique 1 v2 v4 2 1 2
ℒ (q,q˙) −−−−→ ℒ ⇐ ⇒ − αc + --α---+ 𝒪 (-3-) = [− mc ] +--mv
c→+ ∞ 2 c c 2](these37x.png)
 . Le terme entre crochets est constant donc il n’intervient pas dans les équations du
mouvement
. Le terme entre crochets est constant donc il n’intervient pas dans les équations du
mouvement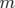 s’exprime finalement
par
s’exprime finalement
par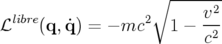

 ) caractérisant l’interaction de la
particule avec le champ électromagnétique
) caractérisant l’interaction de la
particule avec le champ électromagnétique 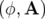 (voir Landau et Lifchitz,
(voir Landau et Lifchitz, 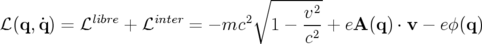
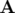 le potentiel vecteur et
le potentiel vecteur et 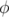 le potentiel scalaire solutions des équations de Maxwell.
le potentiel scalaire solutions des équations de Maxwell.