1.2 Formulation hamiltonienne
Pour établir les équations du mouvement d’une particule circulant dans un accélérateur, nous
partirons du principe de moindre action. Nous commencerons par établir l’expression du Lagrangien
d’une particule libre relativiste de masse 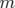 , puis nous plongerons la particule de charge
, puis nous plongerons la particule de charge  dans
un champ électromagnétique (section 1.2.1). Nous en déduirons l’expression générale du
Hamiltonien relativiste que nous exprimerons en coordonnées de l’accélérateur (section 1.2.2). A
chaque étape, nous définirons avec précision l’ensemble des hypothèses réalisées et l’expression
générale du champ magnétique (section 1.2.3).
dans
un champ électromagnétique (section 1.2.1). Nous en déduirons l’expression générale du
Hamiltonien relativiste que nous exprimerons en coordonnées de l’accélérateur (section 1.2.2). A
chaque étape, nous définirons avec précision l’ensemble des hypothèses réalisées et l’expression
générale du champ magnétique (section 1.2.3).
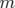 , puis nous plongerons la particule de charge
, puis nous plongerons la particule de charge  dans
un champ électromagnétique (section 1.2.1). Nous en déduirons l’expression générale du
Hamiltonien relativiste que nous exprimerons en coordonnées de l’accélérateur (section 1.2.2). A
chaque étape, nous définirons avec précision l’ensemble des hypothèses réalisées et l’expression
générale du champ magnétique (section 1.2.3).
dans
un champ électromagnétique (section 1.2.1). Nous en déduirons l’expression générale du
Hamiltonien relativiste que nous exprimerons en coordonnées de l’accélérateur (section 1.2.2). A
chaque étape, nous définirons avec précision l’ensemble des hypothèses réalisées et l’expression
générale du champ magnétique (section 1.2.3).