 s’obtiennent à partir du Lagrangien :
s’obtiennent à partir du Lagrangien :
Par définition, les moments canoniques  s’obtiennent à partir du Lagrangien :
s’obtiennent à partir du Lagrangien :
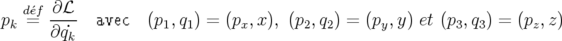 | (1.9) |
soit en utilisant l’expression 1.8 et le facteur de Lorentz 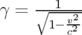 :
:
 | (1.10) |
Le Hamiltonien autonome 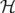 est obtenu à partir de la fonction de Lagrange 1.8 (voir Landau et
Lifchitz, Mécanique, chap. VII) :
est obtenu à partir de la fonction de Lagrange 1.8 (voir Landau et
Lifchitz, Mécanique, chap. VII) :
| ℋ(q,p) |  ∑
k ∑
k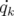  −ℒ(q, −ℒ(q,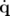 ) ) | ||
= γmv2 + eA ⋅ v − | |||
| = γmc2 + eϕ(q) | (1.11) |
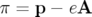 , on établit à partir des équations 1.10 et 1.11
la relation :
L’expression du Hamiltonien 1.11 devient en utilisant la relation 1.12 :
, on établit à partir des équations 1.10 et 1.11
la relation :
L’expression du Hamiltonien 1.11 devient en utilisant la relation 1.12 :
 | (1.13) |
Les équations du mouvement sont les équations dites de Hamilton ou canoniques :
 | (1.14) |
avec la relation supplémentaire si le Hamiltonien dépend explicitement du temps 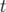 :
:
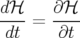 | (1.15) |
Les variables 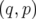 sont appelées variables canoniques. Pour une description du formalisme
Hamiltonien, le lecteur pourra se reporter par exemple au chapitre VII du tome de Mécanique de
Landau et Lifchitz.
sont appelées variables canoniques. Pour une description du formalisme
Hamiltonien, le lecteur pourra se reporter par exemple au chapitre VII du tome de Mécanique de
Landau et Lifchitz.
Pour la suite de l’exposé, il est utile d’obtenir une expression du Hamiltonien pour les jeux de coordonnées cartésiennes et curvilignes. L’obtention générale du Hamiltonien va être présentée en coordonnées curvilignes dont les coordonnées cartésiennes ne sont qu’un cas particulier (la courbure et la torsion sont nulles, cf. infra).
Les coordonnées curvilignes, notées  , sont définies par rapport au repère de
Serret-Frenet direct
, sont définies par rapport au repère de
Serret-Frenet direct 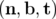 ; une particule de coordonnées transverses
; une particule de coordonnées transverses  et
et  est repérée par son vecteur position
est repérée par son vecteur position  par rapport à l’orbite de référence
par rapport à l’orbite de référence 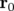 (voir
Fig. 1.3) :
(voir
Fig. 1.3) :
| r(X,Y,s) | = r0(s) + Xn(s) + Y b(s) | (1.16) | |
| = xi + yj + zk |
|
|
Les vecteurs orthonormés  sont respectivement les vecteurs tangent, normal et binormal
définis par :
sont respectivement les vecteurs tangent, normal et binormal
définis par :
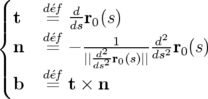 | (1.17) |
où  et
et  décrivent la courbure et la torsion locales de la trajectoire à la longitude
décrivent la courbure et la torsion locales de la trajectoire à la longitude
 :
:
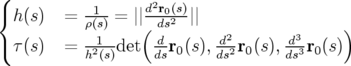 |
Je rappelle les formules de Frenet :
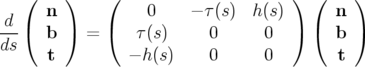 | (1.18) |
On recherche une transformation canonique entre les anciennes variables notées
 et les nouvelles variables
et les nouvelles variables  .
Pour cela, on construit une fonction génératrice dépendant des anciens moments et des
nouvelles positions,
.
Pour cela, on construit une fonction génératrice dépendant des anciens moments et des
nouvelles positions, 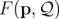 . Les changements de variables sont alors définis implicitement
par :
. Les changements de variables sont alors définis implicitement
par :
| q |  − −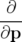 F(p, F(p, ) ) | (1.19a) |
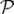 |  − −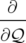 F(p, F(p,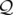 ) ) | (1.19b) |
 | (1.20) |
Par convention la fonction  est choisie nulle. L’équation 1.19b définit les nouveaux moments
recherchés :
est choisie nulle. L’équation 1.19b définit les nouveaux moments
recherchés :
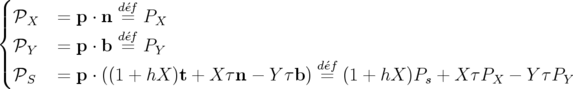 |
avec  les projections usuelles de l’impulsion sur la base
les projections usuelles de l’impulsion sur la base  . On note également
que les coordonnées du potentiel vecteur
. On note également
que les coordonnées du potentiel vecteur  se transforment comme celles du moment
se transforment comme celles du moment  (cf.
équation 1.10).
(cf.
équation 1.10).
Dans la suite, on fait l’hypothèse que la trajectoire de référence est plane, i.e. que la torsion  est nulle2.
En remarquant que la base de Serret-Frenet est orthonormée, le nouveau Hamiltonien s’écrit en
utilisant l’expression 1.13 :
est nulle2.
En remarquant que la base de Serret-Frenet est orthonormée, le nouveau Hamiltonien s’écrit en
utilisant l’expression 1.13 :
| ℋ | (X,Y,s, X, X, Y , Y , s) = ℋ(q( s) = ℋ(q( , ,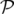 ), p( ), p( , , )) )) | ||
= c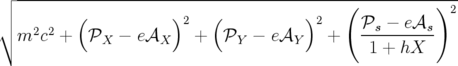 + eϕ( + eϕ(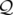 ) ) | (1.21) |
Dans un accélérateur, il est plus commode d’exprimer la trajectoire d’une particule en fonction de la
coordonnée longitudinale prise comme variable indépendante à la place du temps  (
( en
coordonnées rectangulaires ou
en
coordonnées rectangulaires ou  en coordonnées curvilignes).
en coordonnées curvilignes).
Comme nouveau Hamiltonien3,
on choisit 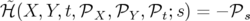 en notant
en notant 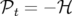 :
:
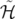 (X, Y,t, (X, Y,t,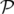 X, X,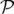 Y , Y ,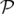 t) = t) = | − (1 + hX) | ||
− e s s | (1.22) |
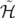 conjugue les couples de variables
conjugue les couples de variables 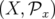 ,
, 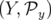 et
et
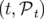 :
:
d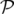 t t − dℋ = − dℋ = | −∑
k=12 − −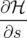 ds − ds −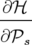 d d s − s − dt dt | ||
⇒−d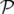 s s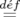 d d = = | ∑
k=12![[ ]
( ∂ℋ ) ( ∂ℋ ) −1 ( ∂ ℋ ) ( ∂ ℋ ) −1
----- ---- d𝒬k + ----- ---- d𝒫k
∂ 𝒬k ∂𝒫s ∂𝒫k ∂𝒫s](these134x.png) | ||
+  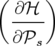 −1dt + −1dt +  −1d −1d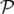 t
t | (1.23) | ||
| par identification en utilisant les équations 1.14, on obtient les nouvelles équations de Hamilton : | |||
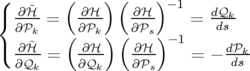 pour k = 1, 2 pour k = 1, 2 | (1.24) | ||
| et | |||
 | (1.25) | ||
La variable  est physiquement reliée à la notion de temps de vol et son moment canonique
est physiquement reliée à la notion de temps de vol et son moment canonique 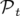 est
l’opposé de l’énergie totale de la particule. Pour la suite des calculs, on suppose que le potentiel électrique
est
l’opposé de l’énergie totale de la particule. Pour la suite des calculs, on suppose que le potentiel électrique
 est nul4.
est nul4.
En faisant l’hypothèse que le potentiel vecteur est nul le long de l’axe optique, i.e. 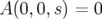 ,
on constate l’existence de la trajectoire particulière :
,
on constate l’existence de la trajectoire particulière : 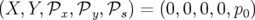 , que l’on
appelle trajectoire de référence.
, que l’on
appelle trajectoire de référence.
La seconde transformation revient simplement à introduire un facteur d’échelle dans les variables :
  | (1.26) |
Pour conserver la nature hamiltonienne des équations, le nouveau Hamiltonien est simplement
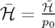 , soit :
, soit :
 | (1.27) |
avec 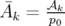 . Le long de la trajectoire de référence, on a alors :
. Le long de la trajectoire de référence, on a alors :
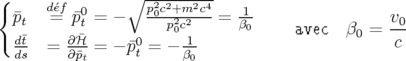 | (1.28) |
Usuellement, on préfère définir le mouvement d’une particule par rapport à une trajectoire de
référence nulle, ce qui nous conduit à faire le dernier changement de variables dépendant de  (d’après Eq. 1.28) :
(d’après Eq. 1.28) :
 | (1.29) |
Ce changement de variables dépend explicitement de  . Si
. Si  est une fonction génératrice, le
nouveau Hamiltonien sera donné par :
est une fonction génératrice, le
nouveau Hamiltonien sera donné par :  . Nous construisons la fonction génératrice
dépendant des anciennes positions et des nouveaux moments
. Nous construisons la fonction génératrice
dépendant des anciennes positions et des nouveaux moments 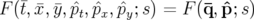 (Dragt et Forest, 1986) :
(Dragt et Forest, 1986) :
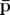 | = 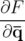  F( F(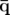 , , ; s) = ; s) =  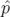 x + x + 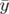 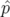 y + y + 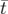 ( (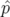 t + t +  ) + G( ) + G(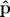 ,s) ,s) | (1.30) |
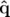 | = 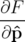  F( F(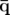 , ,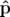 ; s) = ; s) =  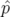 x + x + 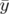  y + y +  ( (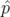 t + t +  ) + ) + 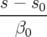  t + K(s) t + K(s) | (1.31) |
 est a priori une fonction quelconque. Pour permettre des comparaisons avec la
littérature, elle est choisie telle que :
est a priori une fonction quelconque. Pour permettre des comparaisons avec la
littérature, elle est choisie telle que :
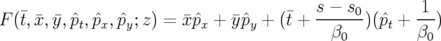 | (1.32) |
On en déduit l’expression du nouveau Hamiltonien  :
:
 | (1.33) |
en remarquant l’identité :  .
.
Dans le cas ultra-relativiste, le Hamiltonien 1.33 se simplifie
encore5
puisque  et
et  . Pour alléger l’écriture, les variables « perdent leur chapeau » (si
aucune confusion n’est possible) et on pose
. Pour alléger l’écriture, les variables « perdent leur chapeau » (si
aucune confusion n’est possible) et on pose  et
et  :
:
 | (1.34) |
Interprétons physiquement les nouvelles variables  et
et  :
:
 représente l’écart à énergie nominale
représente l’écart à énergie nominale  normalisée par l’énergie de la
particule nominale ultra-relativiste.
normalisée par l’énergie de la
particule nominale ultra-relativiste.
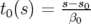 est le temps de passage en
est le temps de passage en  de la particule synchrone. On suppose
que cette dernière se trouve en
de la particule synchrone. On suppose
que cette dernière se trouve en  en
en  . Si
. Si 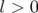 ,
, 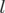 représente l’avance de la
particule par rapport à la particule synchrone.
représente l’avance de la
particule par rapport à la particule synchrone.Lorsqu’on ne s’intéresse pas au cas du solénoïde, le potentiel vecteur n’a qu’une seule
composante non nulle  qui ne dépend que des coordonnées transverses :
qui ne dépend que des coordonnées transverses :
 | (1.35) |
Pour la suite du travail, on a le choix entre conserver cette expression avec la racine carrée et effectuer un développement limité. Dans ce dernier cas, le Hamiltonien se réduit à :
| ℋ | = −(1 + hx)(1 + δ)(1 −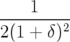 (px2 + p
y2)) − eÂ
s + δ + 1 (px2 + p
y2)) − eÂ
s + δ + 1 | ||
= (1 + hx) − (1 + hx)(1 + δ) − eÂs + δ + 1 − (1 + hx)(1 + δ) − eÂs + δ + 1 |
 | (1.36) |
Cette dernière expression sera utilisée pour déduire la dynamique linéaire. Pour l’instant, il ne reste plus qu’à déterminer l’expression du potentiel vecteur.