 ,
, 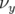 et le nombre d’ondes longitudinale normalisé à
et le nombre d’ondes longitudinale normalisé à  ,
i.e. :
,
i.e. :
La dynamique transverse est modélisée par un système à (2+1) degrés de liberté. La
condition de résonance est obtenue pour une combinaison linéaire entre les nombres
d’ondes transverses  ,
, 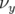 et le nombre d’ondes longitudinale normalisé à
et le nombre d’ondes longitudinale normalisé à  ,
i.e. :
,
i.e. :
 | (1.84) |
Habituellement  est appelé l’ordre de la résonance et correspond à l’ordre des polynômes
du développement du potentiel vecteur. Cependant, il est souvent plus judicieux de définir l’ordre
par l’entier
est appelé l’ordre de la résonance et correspond à l’ordre des polynômes
du développement du potentiel vecteur. Cependant, il est souvent plus judicieux de définir l’ordre
par l’entier 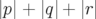 à partir de l’équation :
à partir de l’équation :
![3
p[νx] + q[νy] + r = 0 avec (p,q,r) ∈ ℤ](these393x.png) | (1.85) |
où ![[]](these394x.png) désigne la partie fractionnaire des nombres d’ondes. Cette définition, plus naturelle,
correspond à celle adoptée en Mécanique Céleste. Dans la suite, l’ordre des résonances défini avec
cette convention sera noté par
désigne la partie fractionnaire des nombres d’ondes. Cette définition, plus naturelle,
correspond à celle adoptée en Mécanique Céleste. Dans la suite, l’ordre des résonances défini avec
cette convention sera noté par  .
.
Pour une machine N-périodique, i.e. constituée de  super-périodes, la condition de
résonance est plus stricte : la dynamique de la machine totale est alors la même que pour une seule
super-période avec pour fréquence longitudinale
super-périodes, la condition de
résonance est plus stricte : la dynamique de la machine totale est alors la même que pour une seule
super-période avec pour fréquence longitudinale  .
.
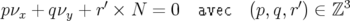 | (1.86) |
Plus un accélérateur a une périodicité élevée, plus la condition de résonance est sévère (cf. Fig. 1.6). Dans la suite, nous parlerons de résonances permises, systématiques ou de structure et de résonances interdites, sous-entendu par la périodicité.
Dans une théorie de perturbation simplement résonante du premier ordre, il peut être montré
que, pour des résonances sommes (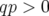 ), la différence des émittances
), la différence des émittances  est conservée.
Pour des résonances différences (
est conservée.
Pour des résonances différences (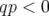 ), c’est la somme des émittances
), c’est la somme des émittances  qui est conservée
(voir par exemple : A General Treatment of Resonances in Accelerators, Guignard, 1978).
Dans le premier cas, il peut y avoir amplification mutuelle des amplitudes d’oscillation
(proportionnelles à la racine carrée de l’émittance), ce qui conduira à la divergence des
trajectoires des particules alors que pour des résonances différences, il ne peut y avoir que
transfert d’amplitudes d’oscillation entre les deux plans. Durant ma thèse, j’ai parfois
entendu dire que les résonances différences ne sont pas dangereuses pour la dynamique du
faisceau. En conséquence, les largeurs des résonances différences ne sont pas toujours
optimisées. Il est clair que ce résultat est celui d’une théorie de perturbation du premier
ordre et qu’il n’est valide qu’au voisinage d’une résonance unique. Proche d’un nœud de
résonances, les largeurs de résonances peuvent se recouvrir et la dynamique est toute
autre.
qui est conservée
(voir par exemple : A General Treatment of Resonances in Accelerators, Guignard, 1978).
Dans le premier cas, il peut y avoir amplification mutuelle des amplitudes d’oscillation
(proportionnelles à la racine carrée de l’émittance), ce qui conduira à la divergence des
trajectoires des particules alors que pour des résonances différences, il ne peut y avoir que
transfert d’amplitudes d’oscillation entre les deux plans. Durant ma thèse, j’ai parfois
entendu dire que les résonances différences ne sont pas dangereuses pour la dynamique du
faisceau. En conséquence, les largeurs des résonances différences ne sont pas toujours
optimisées. Il est clair que ce résultat est celui d’une théorie de perturbation du premier
ordre et qu’il n’est valide qu’au voisinage d’une résonance unique. Proche d’un nœud de
résonances, les largeurs de résonances peuvent se recouvrir et la dynamique est toute
autre.