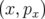 ,
, 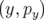 et
et
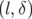 . Cette expression dépend explicitement de la longitude
. Cette expression dépend explicitement de la longitude  prise comme variable
indépendante.
prise comme variable
indépendante.
Nous avons vu page §, l’expression la plus générale du Hamiltonien pour un accélérateur (cf.
Eq. 1.35) exprimée en fonction des trois paires de variables canoniques 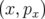 ,
, 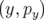 et
et
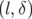 . Cette expression dépend explicitement de la longitude
. Cette expression dépend explicitement de la longitude  prise comme variable
indépendante.
prise comme variable
indépendante.
Dans toute la suite, sauf mention explicite, j’ai choisi de travailler sur la forme quadratique en les impulsions en réalisant un développement limité au premier ordre de la racine carrée. Pour mémoire, je rappelle son expression :
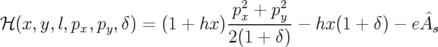 | (2.33) |
La première approximation réalisée a consisté à développer la racine carrée de l’expression 1.35, terme nonlinéaire qui caractérise le fait que les particules sont relativistes. Ce développement permet d’obtenir une expression polynomiale dans les variables accélérateurs. Cette approximation est à la base de nombreux code de tracking. Cependant, il est intéressant de noter que le premier terme négligé est le terme octupolaire,
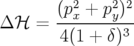 | (2.34) |
c’est un terme purement cinématique6
qui doit néanmoins être pris en compte comme correction quand l’émittance est grande et lorsque la
fonction de Twiss 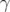 est importante (voir Papaphilippou et Abell, 2000).
est importante (voir Papaphilippou et Abell, 2000).
Dans ce cas, il suffira soit d’introduire des termes d’ordre supérieur du développement limité
de la racine carrée, soit de garder la racine carrée. Ce qui a l’inconvénient majeur de
compliquer les calculs ; de plus, un intégrateur du type 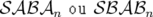 avec correcteur
ne pourra plus être implémenté, car le correcteur
avec correcteur
ne pourra plus être implémenté, car le correcteur 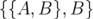 n’est en général plus
intégrable.
n’est en général plus
intégrable.
La deuxième approximation fondamentale concerne l’expression générale du champ magnétique (cf. Eq. 1.46 page §) : on suppose que le champ magnétique est constant à l’intérieur d’un élément et nul à l’extérieur, si bien que le Hamiltonien devient autonome pour un élément donné. En réalité, la transition est plus douce. En anglais, on parle d’approximation hard edge, ce qui signifie que les éléments ont un profil magnétique rectangulaire. Cette approximation ne sera plus suffisante pour les machines de faible rayon de courbure. Pour prendre en compte les champs de fuite, une solution simple consiste à compléter la description des éléments ; nous en discuterons plus en détail au moment d’aborder les éléments dipolaires.
Les équations du mouvement sont données par les équations de Hamilton :
 | (2.35) |
Etrangement, bien que certains éléments (dipôle, quadripôles) soient complètement intégrables à la suite des deux approximations précédentes, l’intégration est généralement réalisée en utilisant une solution approchée au moyen d’un intégrateur symplectique. Une des raisons est que cette démarche est nécessaire si l’on désire obtenir l’application de premier retour de l’anneau et utiliser des méthodes automatiques d’algèbre différentielle (e.g. le DA-Package appelé plus tard Truncated Power Series Algebra — TPSA — développé en FORTRAN77 par Berz en 1989, voir aussi son livre : Modern Map Methods in Particle Beam Physics, 1999 et plus récemment The Full Polymorphic Package qui est une extension écrite en FORTRAN90 par Forest [47]).
Au cours de ce travail, je n’étais pas intéressé — dans un premier temps — par le calcul de l’application de premier retour (analyse globale de l’anneau), c’est pourquoi je conserve la solution exacte si elle existe — sauf temps prohibitifs de calculs, instabilités numériques, rendant l’intégration symplectique plus efficace — De plus, je reste convaincu qu’il est très souvent plus avantageux en termes de temps de calcul d’écrire un code de tracking construit sur le Hamiltonien local de chacun des éléments (au moins pour les machines à rayonnement synchrotron).
Description et Hamiltonien :
La section droite, drift en anglais, est l’élément le plus simple à modéliser dans un accélérateur,
car c’est un élément sans champ magnétique ( ). Elle est caractérisée par un seul
paramètre : sa longueur notée
). Elle est caractérisée par un seul
paramètre : sa longueur notée 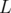 . En coordonnées rectangulaires (
. En coordonnées rectangulaires ( ), son Hamiltonien se
réduit à la forme (cf. Eq. 2.33) :
), son Hamiltonien se
réduit à la forme (cf. Eq. 2.33) :
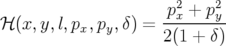 | (2.36) |
Les variables  sont cycliques7,
les équations du mouvement sont :
sont cycliques7,
les équations du mouvement sont :
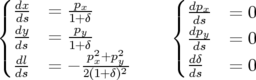 | (2.37) |
Une seule hypothèse de calcul : La linéarité des équations est obtenue par le développement limité du terme cinématique (cf. supra) que j’appelle pour la suite approximation des petits angles.
Intégration des équations : Le système 2.37 est complètement intégrable de solution :
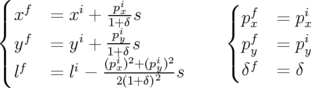 | (2.38) |
où les exposants  et
et 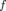 désignent les coordonnées canoniques respectivement à l’entrée et à la
sortie de la section droite de longueur
désignent les coordonnées canoniques respectivement à l’entrée et à la
sortie de la section droite de longueur  .
.
Prise en compte des termes négligés : Si la racine carrée est conservée, les équations du mouvement sont nonlinéaires. Il est néanmoins encore aisé d’intégrer les équations du mouvement en coordonnées rectangulaires ou curvilignes (cf. annexe A.1 et annexe A.3 expression A.36). Il est ainsi possible de vérifier la validité des approximations réalisées.
Un dipôle simple est caractérisé par un rayon de courbure constant 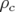 et une longueur
et une longueur 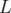 ; en
moyenne, il courbe la trajectoire d’une particule d’un angle
; en
moyenne, il courbe la trajectoire d’une particule d’un angle 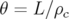 . Son Hamiltonien s’exprime
naturellement en coordonnées curvilignes en utilisant les équations 2.33 et 1.51 :
. Son Hamiltonien s’exprime
naturellement en coordonnées curvilignes en utilisant les équations 2.33 et 1.51 :
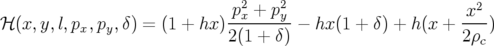 | (2.39) |
Par la suite, je ne distinguerai plus le rayon de courbure 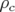 de l’élément et celui introduit par le
système de coordonnées curvilignes (
de l’élément et celui introduit par le
système de coordonnées curvilignes (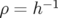 ). Le terme quadratique en
). Le terme quadratique en  de l’expression 2.39
traduit une focalisation horizontale purement géométrique du dipôle.
de l’expression 2.39
traduit une focalisation horizontale purement géométrique du dipôle.
Pour intégrer le Hamiltonien 2.39, je vais me placer dans un cadre un peu plus général. En effet, dans certaines sources de lumière, comme à l’ALS, il existe des dipôles dits combinés, car ils comprennent en plus du terme dipolaire, une composante quadripolaire.
Description et Hamiltonien : Le Hamiltonien d’un dipôle combiné est déduit des équations 2.33, 1.51 et 1.53 :
| ℋ(x,y,l,px,py,δ) | = 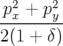 + hx + hx − hx(1 + δ) + h(x + h − hx(1 + δ) + h(x + h ) + ) +  (x2 − y2) (x2 − y2) | ||
= 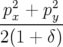 + hx + hx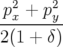 − hδx + h2 − hδx + h2 + +  (x2 − y2) (x2 − y2) | (2.40) |
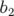 caractérise le gradient quadripolaire. Dans la plupart des
codes de tracking (e.g. BETA [93], DESPOT [42], TRACY [11]), on fait de plus
l’approximation dite des grandes machines en négligeant le terme encadré dans l’équation
ci-dessus8,
de type hexapolaire, qui contribue fortement à la chromaticité des petites machines (Dragt, 1982 et
Forest, 1998). Si bien qu’au final, le Hamiltonien du dipôle combiné est simplement :
caractérise le gradient quadripolaire. Dans la plupart des
codes de tracking (e.g. BETA [93], DESPOT [42], TRACY [11]), on fait de plus
l’approximation dite des grandes machines en négligeant le terme encadré dans l’équation
ci-dessus8,
de type hexapolaire, qui contribue fortement à la chromaticité des petites machines (Dragt, 1982 et
Forest, 1998). Si bien qu’au final, le Hamiltonien du dipôle combiné est simplement :
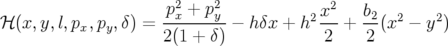 | (2.41) |
On en déduit les équations du mouvement :
 | (2.42) |
Hypothèses de calcul : les approximations (a) des grandes machines, (b) des petits angles et (c) hard edge pour le champ magnétique ont été supposées pour exprimer le Hamiltonien du dipôle combiné sous la forme 2.41.
Intégration exacte des équations : Les équations du mouvement 2.42 sont complètement intégrables (cf. équations de deux oscillateurs harmoniques découplés). La solution exacte est donnée en annexe A.2 (p. §) en termes de fonctions trigonométriques circulaires et hyperboliques.
Intégration approchée des équations : Il est également possible d’utiliser un schéma symplectique pour intégrer le Hamiltonien 2.41 que l’on décompose en deux parties séparément intégrables9 :
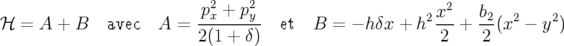 | (2.43) |
Comme annoncé dans la section précédente, ce découpage du Hamiltonien va nous
permettre d’utiliser un intégrateur de classe 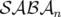 ou de classe
ou de classe 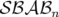 . Quelque
soit le type d’intégrateur choisi, il suffit de savoir évaluer les deux opérateurs
. Quelque
soit le type d’intégrateur choisi, il suffit de savoir évaluer les deux opérateurs 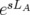 et
et
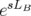 . En fait le calcul est presque immédiat, dans chacun des cas, il y a au plus un seul
crochet de Poisson à calculer. On obtient les applications respectivement pour
. En fait le calcul est presque immédiat, dans chacun des cas, il y a au plus un seul
crochet de Poisson à calculer. On obtient les applications respectivement pour 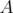 et
et
 :
:
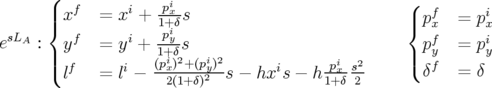 | (2.44) |
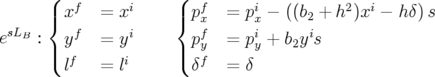 | (2.45) |
Nous avons également vu qu’il est possible d’améliorer l’intégrateur en introduisant un
correcteur (cf. Eq. 2.31). Il suffit de savoir calculer et évaluer le double crochet de Poisson
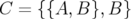 :
:
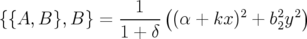 | (2.46) |
avec  et
et  . L’application définie pour le correcteur est alors :
. L’application définie pour le correcteur est alors :
 | (2.47) |
avec  conformément à l’équation 2.31.
conformément à l’équation 2.31.
Correction due aux coins de l’aimant :
|
|
Pour être rigoureux, l’expression du Hamiltonien du dipôle combiné 2.41 décrit un aimant secteur
ou aimant à faces tournées (cf. la définition du bloc courbe page § et le schéma 2.2-a). Souvent, les
aimants d’un accélérateur sont à faces parallèles (e.g. à l’ALS ou Super-ACO), il est donc nécessaire de
corriger les effets de bord introduits par les coins des aimants (cf. Fig. 2.2-b). Au premier ordre, ces
effets se modélisent par un champ quadripolaire focalisant horizontalement et défocalisant
verticalement10.
L’application entre l’entrée et la sortie d’un aimant à faces parallèles est simplement — au premier
ordre — la composition des applications d’un aimant secteur,  , et des coins d’entrée,
, et des coins d’entrée,  ,
et sortie,
,
et sortie, 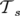 ,
, 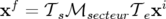 (Forest et al., 1994), soit pour un angle d’entrée ou de sortie
de l’aimant
(Forest et al., 1994), soit pour un angle d’entrée ou de sortie
de l’aimant 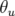 :
:
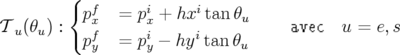 | (2.48) |
Notons que cet effet sera prépondérant pour les petites machines, car il est proportionnel à la
courbure 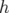 .
.
Pour les machines à faible rayon de courbure comme Super-ACO, un effet supplémentaire est
encore à ajouter dans le modèle : les champs de fuite. Ce phénomène est simplement lié au fait que
le champ magnétique décroît sur les bords de l’aimant et n’est pas tout à fait nul juste à l’extérieur du
dipôle (l’approximation hard-edge doit être complétée). Au premier ordre, les champs de fuite induisent
une composante quadripolaire verticale proportionnelle à la courbure 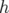 de l’anneau. Le déphasage
vertical11
(
de l’anneau. Le déphasage
vertical11
(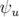 ) est donné par la formule (Brown, 1982, pp. 116–117) :
) est donné par la formule (Brown, 1982, pp. 116–117) :
 | (2.49) |
avec 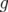 la distance entre les deux pôles de l’aimant,
la distance entre les deux pôles de l’aimant, 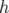 la courbure,
la courbure,  l’angle d’entrée (e) ou de
sortie (s) et
l’angle d’entrée (e) ou de
sortie (s) et 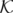 , l’intégrale :
, l’intégrale :
![∫ +∞ By (s)[B0 − By(s)]
𝒦 = ----------2-------ds
−∞ gB 0](these650x.png) | (2.50) |
où 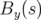 est l’amplitude du champs de fuite sur le plan moyen à la longitude
est l’amplitude du champs de fuite sur le plan moyen à la longitude  mesurée
depuis l’entrée de l’aimant et
mesurée
depuis l’entrée de l’aimant et  est la valeur asymptotique de
est la valeur asymptotique de 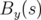 dans l’aimant (cf.
Fig.2.3).
dans l’aimant (cf.
Fig.2.3).
L’application symplectique 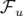 du premier ordre incluant les coins et le champ de fuite de
l’aimant :
du premier ordre incluant les coins et le champ de fuite de
l’aimant :
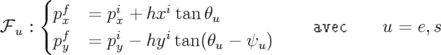 | (2.51) |
Pour un dipôle simple, il suffit de poser  dans les formules établies pour le dipôle
combiné.
En annexe A.2, les équations du mouvement sont intégrées pour différentes approximations et
méthodes d’intégration : (a) sans approximations des grandes machines et des petits angles en
géométrie curviligne et rectangulaire et (b) en prenant en compte le terme des petits
machines.
dans les formules établies pour le dipôle
combiné.
En annexe A.2, les équations du mouvement sont intégrées pour différentes approximations et
méthodes d’intégration : (a) sans approximations des grandes machines et des petits angles en
géométrie curviligne et rectangulaire et (b) en prenant en compte le terme des petits
machines.
Description et Hamiltonien : Un quadripôle droit est un élément magnétique dont la vocation
est de focaliser la particule qui le traverse ; il a une longueur 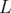 et un gradient magnétique
et un gradient magnétique
 ; son Hamiltonien s’exprime naturellement en géométrie cartésienne à partir des
expressions 2.33 et 1.53 :
; son Hamiltonien s’exprime naturellement en géométrie cartésienne à partir des
expressions 2.33 et 1.53 :
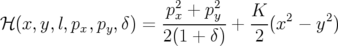 | (2.52) |
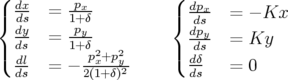
Les équations du mouvement du quadripôle sont (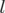 est cyclique) :
est cyclique) :
 | (2.53) |
Hypothèses de calcul : L’expression du Hamiltonien 2.52 est établie dans (a) l’approximation des petits angles et (b) l’approximation hard-edge.
Intégration « exacte » : Les équations du mouvement 2.53 s’intègrent directement pour une
longueur  et pour
et pour 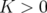 , on obtient :
, on obtient :
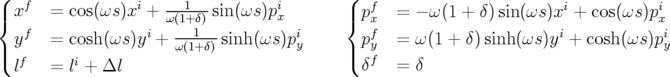 | (2.54) |
avec 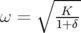 ,
,  et
et
| Δl = |  ω ω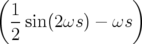 (xi)2 − (xi)2 − ω ω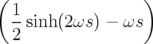 (yi)2 (yi)2 | ||
− 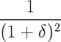 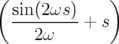 (pxi)2 − (pxi)2 − 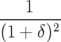 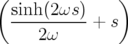 (pyi)2 (pyi)2 | (2.55) | ||
 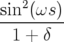 xip
xi − xip
xi − 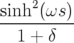 yip
yi yip
yi |
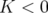 , il suffit de poser
, il suffit de poser  et d’inverser les fonctions
circulaires et hyperboliques dans les équations 2.54. Le quadripôle est alors focalisant dans le plan
vertical.
et d’inverser les fonctions
circulaires et hyperboliques dans les équations 2.54. Le quadripôle est alors focalisant dans le plan
vertical.
Intégrateur symplectique : Les solutions s’écrivent comme celles du dipôle combiné (cf. Eq. 2.44
à 2.47) en posant une courbure nulle, i.e.  .
.
Description et Hamiltonien : Les hexapôles sont inévitablement introduits pour corriger la
chromaticité. Le Hamiltonien d’un hexapôle de force  et de longueur
et de longueur  s’exprime en
utilisant les équations 2.33 et 1.53 en coordonnées rectangulaires par :
s’exprime en
utilisant les équations 2.33 et 1.53 en coordonnées rectangulaires par :
 | (2.56) |
Les équations du mouvement sont (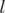 est cyclique) :
est cyclique) :
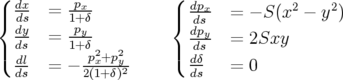 | (2.57) |
Hypothèses de calcul : L’expression du Hamiltonien 2.56 est établie dans (a) l’approximation des
grandes machines, (b) l’approximation hard-edge.
Le schéma d’intégration que nous allons présenter pour l’hexapôle peut simplement se
généraliser pour modéliser un multipôle droit ou tourné quelconque. Par exemple, un 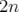 -pôles
droit de force
-pôles
droit de force 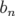 est modélisable par un Hamiltonien de la forme :
est modélisable par un Hamiltonien de la forme :
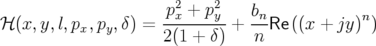 | (2.58) |
Intégration approchée des équations : La partie  contient le Hamiltonien d’une
section droite dont la solution a déjà été calculée (cf. Eq. 2.38). Il ne reste plus qu’à intégrer la
partie
contient le Hamiltonien d’une
section droite dont la solution a déjà été calculée (cf. Eq. 2.38). Il ne reste plus qu’à intégrer la
partie  contenant le potentiel hexapolaire, on obtient l’application :
contenant le potentiel hexapolaire, on obtient l’application :
 | (2.59) |
avec  . Usuellement, l’hexapôle est modélisé par une lentille mince de longueur infinitésimale,
e.g.
. Usuellement, l’hexapôle est modélisé par une lentille mince de longueur infinitésimale,
e.g. 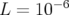 m. Dans ce cas, il suffira de prendre un intégrateur symplectique d’ordre 2. Si
l’hexapôle est modélisé par une lentille épaisse, un intégrateur d’ordre 4 est utilisé comme pour les
éléments magnétiques précédents.
m. Dans ce cas, il suffira de prendre un intégrateur symplectique d’ordre 2. Si
l’hexapôle est modélisé par une lentille épaisse, un intégrateur d’ordre 4 est utilisé comme pour les
éléments magnétiques précédents.