 et en
moments
et en
moments 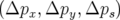 . En suivant l’approche développée par Forest et Hirata (1992), ces
défauts peuvent se modéliser de manière extrêmement simple.
. En suivant l’approche développée par Forest et Hirata (1992), ces
défauts peuvent se modéliser de manière extrêmement simple.
Un élément magnétique peut dévié de son emplacement théorique en position  et en
moments
et en
moments 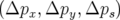 . En suivant l’approche développée par Forest et Hirata (1992), ces
défauts peuvent se modéliser de manière extrêmement simple.
. En suivant l’approche développée par Forest et Hirata (1992), ces
défauts peuvent se modéliser de manière extrêmement simple.
|
|
Par exemple, le schéma A.1 illustre la rotation d’un angle  d’un élément dans le plan x-z. L’application
de transfert de l’élément tourné, notée
d’un élément dans le plan x-z. L’application
de transfert de l’élément tourné, notée  , est obtenue comme la composition de trois applications
de base1
(Forest, 1998, chapitre 10) :
, est obtenue comme la composition de trois applications
de base1
(Forest, 1998, chapitre 10) :
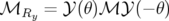 | (A.34) |
où 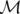 est l’application de transfert de l’élément et
est l’application de transfert de l’élément et 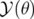 l’application décrivant une rotation
d’axe
l’application décrivant une rotation
d’axe 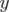 et d’angle
et d’angle 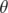 .
.
L’application 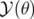 peut être considérée comme une rotation de générateur
peut être considérée comme une rotation de générateur 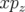 , soit (op.
cit.) :
, soit (op.
cit.) :
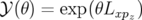 | (A.35) |
avec  et
et  la dérivée de Lie.
la dérivée de Lie.
L’évaluation de l’opérateur A.35 est obtenue en posant  dans le cas du dipôle exact en
géométrie curviligne (Eq. A.6 à A.10), dit différemment elle correspond à l’application de transfert
d’une section droite exprimée en géométrie curviligne. Cette application a été introduite la
première fois par Dragt (1982) :
dans le cas du dipôle exact en
géométrie curviligne (Eq. A.6 à A.10), dit différemment elle correspond à l’application de transfert
d’une section droite exprimée en géométrie curviligne. Cette application a été introduite la
première fois par Dragt (1982) :
 | (A.36) |
avec 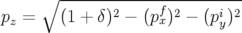 . On remarquera que les applications A.36 et A.14 sont
identiques.
. On remarquera que les applications A.36 et A.14 sont
identiques.
Une rotation d’axe  serait modélisée par l’opérateur
serait modélisée par l’opérateur  . L’application
résultante est la même que celle obtenue pour
. L’application
résultante est la même que celle obtenue pour 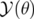 en inversant les rôles de
en inversant les rôles de  et
et  , et de
, et de 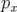 et
et
 dans les formules A.36. Enfin, une rotation d’axe
dans les formules A.36. Enfin, une rotation d’axe  a pour générateur
a pour générateur  , donc
, donc
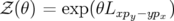 .
.
De manière similaire pour un défaut d’alignement horizontal  , l’application de transfert
, l’application de transfert
 d’un élément sera modélisée par la composition de trois applications comme (Forest, 1998,
chapitre 10) :
d’un élément sera modélisée par la composition de trois applications comme (Forest, 1998,
chapitre 10) :
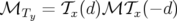 | (A.37) |
avec 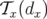 l’opérateur de translation dont le générateur est
l’opérateur de translation dont le générateur est 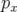 :
:
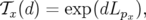 | (A.38) |
et 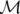 est l’application de transfert de l’élément parfait.
est l’application de transfert de l’élément parfait.
Les translations verticale et longitudinale ont pour générateurs respectivement 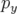 et
et  ,
soit :
,
soit :
| 𝒯y(d) | = exp(dLpy), | (A.39) |
| 𝒯z(d) | = exp(dLpz), | (A.40) |