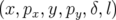 .
.
J’ai annoncé page §, que le dipôle est complètement intégrable. Le but de section est de le
montrer. Les équations sont toujours exprimées en fonctions des variables canoniques
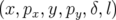 .
.
Description et Hamiltonien : Pour la présente annexe, le dipôle est décrit en introduisant le
cœfficient  qui dans la majorité des cas est égal à la courbure
qui dans la majorité des cas est égal à la courbure  (Forest et al., 1994). Cette
expression est néanmoins utile pour déduire l’expression d’une rotation en géométrie curviligne (cf.
infra). Le Hamiltonien retenu est celui établi page § avec le potentiel vecteur donné par la
formule 1.51 :
(Forest et al., 1994). Cette
expression est néanmoins utile pour déduire l’expression d’une rotation en géométrie curviligne (cf.
infra). Le Hamiltonien retenu est celui établi page § avec le potentiel vecteur donné par la
formule 1.51 :
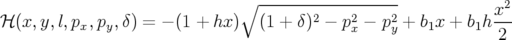 | (A.4) |
Les équations du mouvement deviennent :
 | = px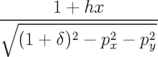 | (A.5a) |
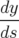 | = py | (A.5b) |
 | = −(1 + δ)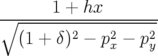 | (A.5c) |
 | = h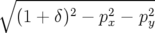 − b1(1 + hx) − b1(1 + hx) | (A.5d) |
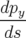 | = 0 | (A.5e) |
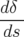 | = 0 | (A.5f) |
Hypothèse de calcul : La seule hypothèse est l’approximation hard-edge. Le Hamiltonien A.4 est complètement intégrable.
Intégration exacte : Les variables  et
et  sont cycliques, donc leurs moments conjugués
respectifs sont constants :
sont cycliques, donc leurs moments conjugués
respectifs sont constants :
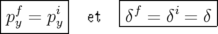 | (A.6) |
L’intégration des autres variables se fait par étapes successives. On commence par l’équation
différentielle de  en utilisant les expressions (Eq. A.5d) puis (Eq. A.5b) :
en utilisant les expressions (Eq. A.5d) puis (Eq. A.5b) :
| dpx | = h ds − b1(1 + hx)ds ds − b1(1 + hx)ds | ||
= 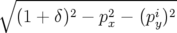 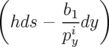 | |||
| yf | = yi +  ∫ ∫
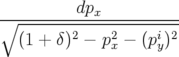 + +  ∫
hds ∫
hds | ||
yf = yi +   + + 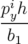 s s | (A.7) |
 |
On déduit alors la solution pour 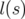 en comparant les équations A.5b et A.5c :
en comparant les équations A.5b et A.5c :
lf = li + 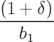  + +  s s | (A.8) | ||
| L’équation différentielle A.5d pour px(s) s’intégre en se servant des expressions A.5a et A.5c : | |||
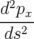 = = | − hpx  − b1h − b1h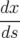 | ||
| = | − h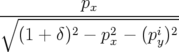 ![[ ∘ -------2----2----i-2 ]
h (1 + δ) + p x − (py) − b1(1 + hx )](these2506x.png) | ||
+ b1hpx | |||
| soit après simplification : | |||
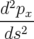 | = −h2p x2 ⇒ p x = a cos(hs) + b sin(hs) | ||
| où les constantes a et b sont déterminées en fonction des conditions initiales, soit : | |||
pxf = p
xi cos(hs) + 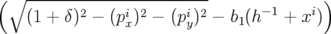 sin(hs) sin(hs) | (A.9) | ||
| L’intégration de la dernière équation (x(s)) est alors immédiate : | |||
 | = h − b1(h−1 + xf) − b1(h−1 + xf) | ||
xf =   | (A.10) | ||