 peut être intégrée sans aucune approximation en coordonnées
rectangulaires ou curvilignes. Ces résultats permettront de pouvoir de vérifier la validité des
approximations réalisées, i.e. le développement Taylor usuel de la racine carrée.
peut être intégrée sans aucune approximation en coordonnées
rectangulaires ou curvilignes. Ces résultats permettront de pouvoir de vérifier la validité des
approximations réalisées, i.e. le développement Taylor usuel de la racine carrée.
La section droite de longueur  peut être intégrée sans aucune approximation en coordonnées
rectangulaires ou curvilignes. Ces résultats permettront de pouvoir de vérifier la validité des
approximations réalisées, i.e. le développement Taylor usuel de la racine carrée.
peut être intégrée sans aucune approximation en coordonnées
rectangulaires ou curvilignes. Ces résultats permettront de pouvoir de vérifier la validité des
approximations réalisées, i.e. le développement Taylor usuel de la racine carrée.
Hamiltonien : Son expression est rappelée en coordonnées rectangulaires (cf. Eq. 1.35 p. § avec
 et
et  ) :
) :
 | (A.1) |
avec pour équations du mouvement :
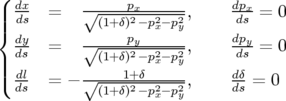 | (A.2) |
Intégration des équations : Les variables 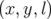 sont encore cycliques, et l’on
obtient :
sont encore cycliques, et l’on
obtient :
 | (A.3) |
avec  la longueur de la section droite.
la longueur de la section droite.