![[ au(s) − |ηu(s)δ|2]
Au = π ---------------- avec u = x,y
βu(s) min](these403x.png)
L’acceptance physique est par définition l’aire de la plus grande ellipse que l’accélérateur accepte (cf. Eq. 1.72) :
|
| (1.87) |
et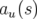 
, la demi-ouverture physique et 
la dispersion locale.
L’acceptance dynamique est définie comme la plus grande région de l’espace des phases (dimension 6) à l’intérieur de laquelle les trajectoires de particules sont bornées, ceci en ne considérant que la dynamique d’une particule isolée. Restreinte à l’espace transverse, on parle d’ouverture dynamique, restreinte à la dynamique longitudinale, d’acceptance en énergie ou RF.
La détermination des dimensions de l’ouverture dynamique est fondamentale mais non triviale.
Sa définition dépend du nombre de tours d’intégration des orbites. Par exemple Irwin (in Chao et
Tigner, pp. 87–91) donne comme nombre de tours optimum, vingt-cinq pour cent du temps
d’amortissement du faisceau, soit environ 1 000 tours pour des électrons. Cette limite est cependant
trop faible pour étudier finement la dynamique à long terme (estimation de la diffusion,
coefficients de Lyapunov), car les trajectoires des particules peuvent diverger aussi bien
au bout d’un très faible nombre de tours (diffusion rapide) que lentement (diffusion
d’Arnold) comme nous le verrons plus tard. La définition de l’ouverture dynamique dépend
aussi des phases auxquelles elle est tracée (généralement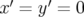 
), car les orbites se
déforment.
Un problème ouvert est actuellement la recherche d’un facteur de qualité pour l’optimisation de l’ouverture dynamique (voir Todesco, 1999).
De par les nonlinéarités, il n’existe pas de méthode analytique générale pour optimiser l’ouverture dynamique. Je présente ici le processus empirique d’optimisation d’une maille utilisé pour le Projet SOLEIL (Nghiem et al., 1997) ; c’est un processus en quatre étapes :
La première étape consiste à choisir un point de fonctionnement dans une région du diagramme des nombres d’ondes (cf. Fig. 1.6) où non seulement, une émittance faible peut être obtenue mais aussi où il y a un minimum de résonances systématiques. Il est en particulier primordial d’éviter la proximité (a) des résonances d’ordres entiers qui sont excitées par les erreurs d’orbite fermée ; (b) des résonances d’ordres demi-entiers qui sont excitées par les erreurs de gradients quadripolaires ; (c) des résonances sommes pour éviter l’amplification mutuelle des oscillations bétatrons horizontales et verticales ; (d) des résonances du troisième ordre qui sont introduites par les hexapôles. Ces critères permettent d’obtenir une ouverture dynamique peu sensible aux défauts magnétiques et à l’introduction des insertions.
La deuxième étape concerne l’optimisation des fonctions
bétatrons10 :
(a) la fonct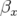ion 
doit être minimum dans les dipôles pour obtenir une faible émittance ; (b) la
création de hautes brillances issues des insertions contraint la fonction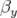 
; (c) le rapport
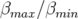doit être minimum pour l’injection du faisceau ; de plus les fonctions bétatrons ne
doivent pas être trop grandes pour éviter d’avoir une sensibilité trop importante aux
erreurs magnétiques. Il est également souhaitable de conserver la symétrie la plus élevée
possible.
La troisième étape est le positionnement des hexapôles dans la maille. Les forces hexapolaires
doivent être les plus faibles possibles, car elles limitent l’ouverture dynamique. Les hexapôles sont
placés dans les régions à grande dispersion où les fonctions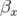 
et 
sont découplées
(Eq. 1.79).
La quatrième et dernière étape est dédiée à la correction de la chromaticité et l’optimisation de
l’ouverture dynamique proprement dit. Seule l’ouverture dynamique on momentum (
) est
optimisée. La minimisation des résonances hexapolaires d’ordre 3 est fondée sur une méthode
analytique du premier ordre (voir la thèse de Audy, 1989).