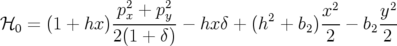
Dans un accélérateur, la solution des équations transverses du mouvement peut se décomposer en deux termes, (a) l’orbite fermée qui, par définition, est une orbite de période 1 et (b) une oscillation de faible amplitude dite bétatron autour de cette orbite fermée. Nous verrons que l’orbite fermée dépend de l’énergie de la particule. Mais tout d’abord établissons les équations linéaires du mouvement.
Pour cela, nous partons de l’expression du Hamiltonien 1.36 que nous réécrivons en ne conservant que les parties linéaire et quadratique du potentiel vecteur 1.46, i.e. le potentiel d’un dipôle 1.51 et celui d’un quadripôle droit 1.53 :
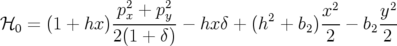 | (1.54) |
Les équations du mouvement transverse sont alors :
 | (1.55) |
Pour l’instant, nous adoptons les approximations classiques afin de retrouver les expressions données par la littérature, à savoir :
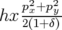 dans
l’expression du Hamiltonien 1.54
dans
l’expression du Hamiltonien 1.54
 .
.Le Hamiltonien 1.54 devient en prenant en compte la première approximation classique :
 | (1.56) |
Les équations du mouvement 1.55 s’écrivent comme :
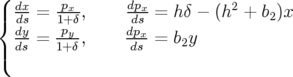 | (1.57) |
Soit en termes d’équations différentielles du second ordre des variables  et
et 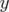 (en négligeant les
termes d’ordre 2 en
(en négligeant les
termes d’ordre 2 en 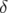 ) :
) :
 | (1.58) |
Nous remarquerons les points suivants :
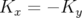 et
et  ;
;
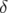 de la particule ;
de la particule ;
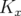 et
et 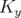 sont définies par morceaux à valeur constante dans chaque
élément magnétique et L-périodiques7
pour une machine de circonférence
sont définies par morceaux à valeur constante dans chaque
élément magnétique et L-périodiques7
pour une machine de circonférence 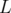 ;
;
Dans la suite, j’emploierai les anglicismes : particule on momemtum si  et particule off
momemtum si
et particule off
momemtum si 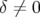 . Le symbole
. Le symbole  désigne la dérivation par rapport à la longitude
désigne la dérivation par rapport à la longitude  et
et  la
dérivée seconde.
la
dérivée seconde.
L’équation homogène du système 1.58 peut être réécrite pour  comme l’équation
générique :
comme l’équation
générique :
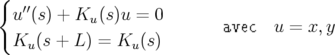 | (1.59) |
C’est donc une équation de Hill.
La solution générale 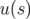 de l’équation de Hill 1.59 décrit le mouvement d’une particule
d’énergie nominale de la machine, i.e.
de l’équation de Hill 1.59 décrit le mouvement d’une particule
d’énergie nominale de la machine, i.e.  . Usuellement, la solution s’écrit de différentes
manières dans la littérature :
. Usuellement, la solution s’écrit de différentes
manières dans la littérature :
– en utilisant le théorème de Floquet (voir par exemple Courant et Snyder, 1958), la solution
s’exprime en fonction de la fonction bétatron 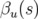 :
:
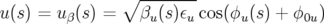 | (1.60) |
avec la phase  ,
, 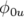 la phase à l’origine et
la phase à l’origine et 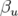 vérifiant l’équation
différentielle :
vérifiant l’équation
différentielle :
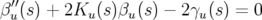 | (1.61) |
en posant  et
et  . Les paramètres
. Les paramètres  ,
, 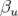 et
et 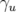 sont appelés fonctions ou
paramètres de Twiss. L’avance de phase sur un tour complet ramenée à
sont appelés fonctions ou
paramètres de Twiss. L’avance de phase sur un tour complet ramenée à 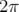 définit le nombre
d’ondes
définit le nombre
d’ondes 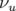 :
:
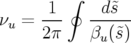 | (1.62) |
qui correspond au nombre moyen d’oscillations effectuées par la particule autour de l’orbite fermée.
L’invariant linéaire, aussi appelé invariant de Courant-Snyder ou encore émittance, est l’intégrale première du mouvement :
 | (1.63) |
Géométriquement, l’équation 1.63 est celle d’une ellipse d’aire  dans le plan
dans le plan  (cf.
Fig. 1.5).
(cf.
Fig. 1.5).
|
|
– en utilisant la paramétrisation de Courant-Snyder (1958) :
 | (1.64) |
où 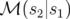 est la matrice de transfert de la longitude
est la matrice de transfert de la longitude 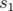 à
à 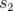 ,
,  l’avance de phase entre
l’avance de phase entre 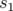 à
à 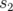 ,
, 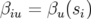 . Sur un tour complet, l’expression 1.64 se simplifie pour donner l’application
linéaire de premier retour :
. Sur un tour complet, l’expression 1.64 se simplifie pour donner l’application
linéaire de premier retour :
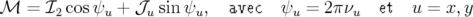 | (1.65) |
avec 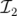 la matrice identité et
la matrice identité et
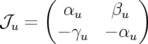 | (1.66) |
– en utilisant les fonctions principales 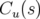 et
et 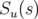 qui par définition sont deux solutions
indépendantes de l’équation de Hill 1.59 vérifiant :
qui par définition sont deux solutions
indépendantes de l’équation de Hill 1.59 vérifiant :
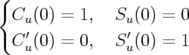 | (1.67) |
La solution générale avec pour conditions initiales  peut alors s’écrire (Courant et Snyder,
1958) :
peut alors s’écrire (Courant et Snyder,
1958) :
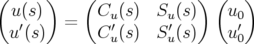 | (1.68) |
Pour une particule n’ayant pas l’énergie nominale du faisceau, i.e. 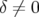 , l’équation 1.58
devient :
, l’équation 1.58
devient :
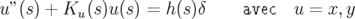 | (1.69) |
Par convention, on appelle fonction dispersion la solution particulière 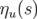 périodique pour
périodique pour
 de l’équation 1.69. En utilisant les fonctions principales
de l’équation 1.69. En utilisant les fonctions principales 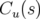 et
et  , la dispersion
linéaire est donnée par la formule (Lee, 1998) :
, la dispersion
linéaire est donnée par la formule (Lee, 1998) :
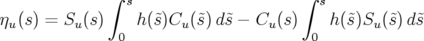 | (1.70) |
En utilisant la linéarité des équations, on en déduit que la solution complète peut s’exprimer par :
| u(s) | =  cos(ϕu(s) + ϕu0) + ηu(s)δ cos(ϕu(s) + ϕu0) + ηu(s)δ | (1.71) |
| = uβ(s) + uδ(s) | (1.72) |
 la solution bétatron et
la solution bétatron et 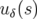 l’orbite fermée chromatique.
l’orbite fermée chromatique.
Similairement à l’optique géométrique où une lentille focalise plus faiblement les photons de
petite longueur d’onde, i.e. de grande énergie, la focalisation d’un quadripôle est une fonction
intrinsèquement dépendante de l’énergie ( ). Si
). Si 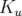 est le gradient quadripolaire, alors on peut
écrire (cf. Eq. 1.58) :
est le gradient quadripolaire, alors on peut
écrire (cf. Eq. 1.58) :
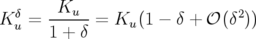 | (1.73) |
Donc, les particules ayant une énergie supérieure à l’énergie nominale 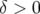 sont moins focalisées.
Il s’ensuit que l’avance de phase dans un élément quadripolaire devient une fonction de l’énergie, ce
qui nous conduit à définir la chromaticité comme la variation du nombre d’ondes,
sont moins focalisées.
Il s’ensuit que l’avance de phase dans un élément quadripolaire devient une fonction de l’énergie, ce
qui nous conduit à définir la chromaticité comme la variation du nombre d’ondes, 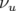 , en fonction
de l’énergie :
, en fonction
de l’énergie :
 | (1.74) |
Suivant les cas, nous parlerons de chromaticité [globale] ou de chromaticité réduite, i.e. ramenée au
nombre d’ondes  . La contribution produite uniquement par les éléments linéaires, i.e. les
dipôles et les quadripôles est appelée chromaticité naturelle. Elle est toujours négative et a des
conséquences très dommageables sur la dynamique globale du faisceau si elle n’est pas corrigée.
Par exemple pour SOLEIL, les chromaticités naturelles sont
. La contribution produite uniquement par les éléments linéaires, i.e. les
dipôles et les quadripôles est appelée chromaticité naturelle. Elle est toujours négative et a des
conséquences très dommageables sur la dynamique globale du faisceau si elle n’est pas corrigée.
Par exemple pour SOLEIL, les chromaticités naturelles sont  et
et
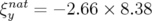 , ce qui induit pour
, ce qui induit pour  % les déplacements des nombres d’ondes proches
du demi-entier
% les déplacements des nombres d’ondes proches
du demi-entier  . Ces glissements des nombres d’ondes peuvent amener le
faisceau sur des lignes de résonance et conduire à des conséquences néfastes pour les performances
de l’anneau.
. Ces glissements des nombres d’ondes peuvent amener le
faisceau sur des lignes de résonance et conduire à des conséquences néfastes pour les performances
de l’anneau.
La seconde raison nécessitant une correction de chromaticité provient des effets collectifs. Lorsqu’un paquet de particules circule dans l’accélérateur, les particules de tête laissent derrière elles un champ de sillage qui va être ressenti par les particules de queue du paquet et induire des instabilités. Au bout d’une demi-période synchrotron, les particules de tête deviennent les particules de queue et réciproquement. Ce type d’instabilité, dite head-tail, peut conduire à la perte du faisceau. Il peut être montré (voir par exemple Lee, 1998) que ces instabilités disparaissent à chromaticités nulles et sont plus néfastes pour des chromaticités négatives que positives.
Dans un anneau de stockage, la chromaticité doit être soit nulle soit légèrement positive. Pour la compenser, on introduit dans l’anneau des éléments nonlinéaires : les hexapôles8.