 à
à 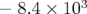 en
modifiant les réglages hexapolaires. Cependant la dynamique du faisceau est complètement modifiée
(cf. Fig. 3.36). Nous nous attarderons sur la comparaison des deux optiques.
en
modifiant les réglages hexapolaires. Cependant la dynamique du faisceau est complètement modifiée
(cf. Fig. 3.36). Nous nous attarderons sur la comparaison des deux optiques.
Le second jeu hexapolaire est une tentative d’optimisation du point de
fonctionnement précédent (pas d’améliorations expérimentales notables sauf à fort
courant18).
Seule la pente à l’origine de la courbe en fréquence est modifiée de  à
à 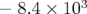 en
modifiant les réglages hexapolaires. Cependant la dynamique du faisceau est complètement modifiée
(cf. Fig. 3.36). Nous nous attarderons sur la comparaison des deux optiques.
en
modifiant les réglages hexapolaires. Cependant la dynamique du faisceau est complètement modifiée
(cf. Fig. 3.36). Nous nous attarderons sur la comparaison des deux optiques.
|
|
L’ouverture dynamique (cf. Fig. 3.36) est encore plus grande que celle obtenue pour le premier
réglage (cf. Fig. 3.28) : ![[− 80,45]y=0 × [− 15,15]x=0](these1412x.png) mm, plus régulière mais elle est
toujours surestimée. Comme précédemment, la carte en fréquence (Fig. 3.37, voir aussi les
cartes en couleur B.11) présente un repliement et peut être scindée en deux parties
(Fig. 3.38) :
mm, plus régulière mais elle est
toujours surestimée. Comme précédemment, la carte en fréquence (Fig. 3.37, voir aussi les
cartes en couleur B.11) présente un repliement et peut être scindée en deux parties
(Fig. 3.38) :
![[− 30, 20] × [− 8, 8]](these1413x.png) mm dans l’espace des configurations, avec un
glissement des nombres d’ondes très faible (
mm dans l’espace des configurations, avec un
glissement des nombres d’ondes très faible ( ). Cette partie est
extrêmement régulière et pratiquement exempte de résonances avec peu de diffusion.
). Cette partie est
extrêmement régulière et pratiquement exempte de résonances avec peu de diffusion.
 ne soit
jamais atteinte, la résonance d’ordre 5,
ne soit
jamais atteinte, la résonance d’ordre 5,  est déjà fortement
excitée pour une machine idéale puisqu’elle capture toutes les particules de conditions
initiales
est déjà fortement
excitée pour une machine idéale puisqu’elle capture toutes les particules de conditions
initiales ![x ∈ [− 74, − 42] ∪ [32, 35]](these1417x.png) mm.
mm.De manière générale pour ce réglage, la dynamique est moins « compliquée » et beaucoup plus
stable. Le glissement des nombres d’ondes avec l’amplitude est plus faible, si bien que la résonance
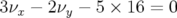 est atteinte à une amplitude
est atteinte à une amplitude  mm soit aussi grande que l’ouverture
physique (
mm soit aussi grande que l’ouverture
physique (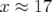 mm pour le premier réglage hexapolaire).
mm pour le premier réglage hexapolaire).
|
|
Deux orbites particulières ont été intégrées pour illustrer la diffusion au voisinage d’une résonance dans une zone de mouvement régulier et irrégulier (Fig. 3.40-a,b) :
La première orbite (O1) correspond aux conditions initiales  mm avec
pour nombres d’ondes initiaux
mm avec
pour nombres d’ondes initiaux 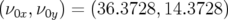 . L’intégration est réalisée sur 1
million de tours, les fréquences sont recalculées tous les 1 000 tours ; la particule oscille rapidement
transversalement à la résonance
. L’intégration est réalisée sur 1
million de tours, les fréquences sont recalculées tous les 1 000 tours ; la particule oscille rapidement
transversalement à la résonance  et lentement longitudinalement (voir aussi
Fig. 3.39).
et lentement longitudinalement (voir aussi
Fig. 3.39).
|
|
La seconde orbite (O2) est perdue au bout de 38 026 tours de l’anneau. Ses conditions initiales
en amplitudes et en fréquences sont 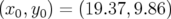 mm et
mm et 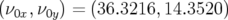 ,
soit au voisinage de la résonance
,
soit au voisinage de la résonance  . La particule y reste environ 15 000
tours avant de diffuser rapidement L’évolution de la partie fractionnaire des nombres d’ondes avec le
nombre de tours est donné par la figure 3.40-b.
. La particule y reste environ 15 000
tours avant de diffuser rapidement L’évolution de la partie fractionnaire des nombres d’ondes avec le
nombre de tours est donné par la figure 3.40-b.
Comme pour le premier réglage, les valeurs réduites des chromaticités sont légèrement positives
( et
et  ). Le glissement des nombres d’ondes avec l’énergie
). Le glissement des nombres d’ondes avec l’énergie 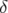 est illustré par la
figure 3.42.
est illustré par la
figure 3.42.
Les cartes en fréquence ont été tracées pour des écarts à l’énergie nominale compris entre
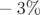 et
et 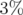 (Fig. 3.41) en considérant toujours une machine parfaite.
(Fig. 3.41) en considérant toujours une machine parfaite.
|
|
L’ouverture dynamique diminue avec  (cf. Fig. 3.43) ; cette diminution est plus importante
pour des écarts à l’énergie positifs.
(cf. Fig. 3.43) ; cette diminution est plus importante
pour des écarts à l’énergie positifs.
L’allure et le repliement des cartes varient beaucoup avec  . Pour de grands écarts en énergie,
les cartes sont pratiquement « plates » ; notons cependant que pour
. Pour de grands écarts en énergie,
les cartes sont pratiquement « plates » ; notons cependant que pour  , les nombres d’ondes
diminuent avec l’amplitudes (distances au centre du faisceau) alors que pour
, les nombres d’ondes
diminuent avec l’amplitudes (distances au centre du faisceau) alors que pour 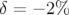 , ils
augmentent avec l’amplitude.
, ils
augmentent avec l’amplitude.
|
|
Pour 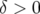 , la résonance d’ordre 5,
, la résonance d’ordre 5,  est atteinte beaucoup plus tôt, et surtout,
la résonance
est atteinte beaucoup plus tôt, et surtout,
la résonance  , systématique d’ordre 4 et destructive ici, limite la dynamique ; ce
qui explique la diminution drastique de plus de 50 % de l’ouverture dynamique entre
0% et +2%. Par contre au-delà de +3%, la résonance
, systématique d’ordre 4 et destructive ici, limite la dynamique ; ce
qui explique la diminution drastique de plus de 50 % de l’ouverture dynamique entre
0% et +2%. Par contre au-delà de +3%, la résonance  n’est plus destructive
pour une machine idéale : l’ouverture dynamique est de nouveau plus grande (frontière
2.3%).
n’est plus destructive
pour une machine idéale : l’ouverture dynamique est de nouveau plus grande (frontière
2.3%).
Pour  , de nouvelles résonances de couplages (Tab. 3.13) apparaissent de par le
déplacement du point de fonctionnement avec l’énergie.
, de nouvelles résonances de couplages (Tab. 3.13) apparaissent de par le
déplacement du point de fonctionnement avec l’énergie.
|
Comme annoncé précédemment, les résonances 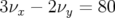 et
et  ont une grande
amplitude qu’il faudrait essayer de réduire pour améliorer l’ouverture dynamique pour
ont une grande
amplitude qu’il faudrait essayer de réduire pour améliorer l’ouverture dynamique pour
 .
.
Pour  , l’extension des cartes en fréquence est plus importante que pour l’énergie
nominale. D’autres résonances vont alors dominer dans la dynamique aux différentes
amplitudes.
, l’extension des cartes en fréquence est plus importante que pour l’énergie
nominale. D’autres résonances vont alors dominer dans la dynamique aux différentes
amplitudes.
L’acceptance dynamique diminue avec  , mais dans le pire des cas elle reste comparable avec
l’acceptance physique.
, mais dans le pire des cas elle reste comparable avec
l’acceptance physique.
La surcompensation de la chromaticité a l’inconvénient majeur de compliquer l’optimisation, puisque les points de fonctionnement dépendent fortement de l’énergie de la particule. Idéalement, il faudrait pouvoir optimiser la dynamique aux différentes énergies.
La durée de vie Touschek est calculée de la même manière que pour le premier réglage hexapolaire. Les résultats sont rassemblés dans le tableau 3.14 (voir aussi les figures 3.44-a et b).
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
En comparant les durées de vie Touschek obtenues pour les deux réglages hexapolaires de
l’ESRF (Fig. 3.34 et Fig. 3.44), nous constatons que le second réglage est meilleur. Ce résultat se
comprend bien si l’on se rappelle que la dynamique off momentum du premier réglage est fortement
marquée par la résonance entière  , si bien qu’il faut prendre en compte dans les calculs
l’ouverture dynamique off momentum qui est alors le facteur limitatif. Ces résultats tendraient à
corroborer les mesures expérimentales. Il faut toutefois reconnaître que les durées de vie mesurées
sont bien plus faibles.
, si bien qu’il faut prendre en compte dans les calculs
l’ouverture dynamique off momentum qui est alors le facteur limitatif. Ces résultats tendraient à
corroborer les mesures expérimentales. Il faut toutefois reconnaître que les durées de vie mesurées
sont bien plus faibles.