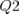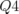Etude préliminaire

5.1.3 Etude préliminaire

Pour le début de l’étude, on ne considère que les 32 correcteurs situés dans les quadripôles. Pour s’aﬀranchir des nonlinéarités, les hexapôles et les lentilles décapolaires sont éteints. Dans un premier temps, on a voulu s’assurer que si l’on donne à LOCO comme matrice expérimentale la matrice théorique alors LOCO donne l’ajustement parfait.

5.1.3.1 Conditions du test

L’ajustement est réalisé uniquement sur les gradients des quatre familles de quadripôles 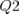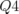$Q1$ , $Q2$ , $Q3$ , $Q4$ . La fonction dispersion est supposée nulle tout autour de la machine pour s’aﬀranchir du facteur d’Amman (cf. infra).

5.1.3.2 Résultats

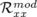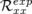Au bout de deux itérations, l’algorithme converge. Les petits écarts observés s’expliquent par le nombre de chiﬀres signiﬁcatifs entrés dans la matrice-réponse expérimentale simulée en tant que modèle. A la lecture du tableau 5.1, les valeurs rms résiduelles sont négligeables compte tenu de la précision (arrondis à deux chiﬀres signiﬁcatifs). $mod ℛxx$ et $exp ℛxx$ (resp. $mod ℛyy$ et $exp ℛ yy$ ) sont les valeurs rms en millimètres des matrices-réponse théorique et expérimentale horizontales (resp. verticales). 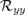$Δ$ $ℛxx$ et $Δ$ $ℛyy$ donnent l’écart rms entre ces matrices.


	Q1[K1]	Q2[K1]	Q3[K1]	Q4[K1]	$νx$	$νy$

Initiaux	-1.46335	2.60629	2.47828	-1.41897	4.72512	1.69845
Finaux	-1.46318	2.60580	2.47878	-1.41907	4.72550	1.69821
Ecarts rel.	-1.1E-4	1.8E-4	-2.0E-4	-6.9E-5	8.0E-5	-1.4E-4

rms	$ℛmxoxd$	$ℛexxpx$	$Δ$ $ℛxx$	$ℛmoydy$	$ℛexyyp$	$Δ$ $ℛyy$

Initiaux	2.1834	2.1847	0.54251E-2	1.4959	1.4950	0.54259E-2
Finaux	2.1846	2.1847	0.47406E-2	1.4953	1.4950	0.52990E-2

TAB. 5.1:

Ajustement modèle sur modèle : variation des gradients quadripolaire $K1$ de chacune des 4 familles quadripolaires $Qi$ de Super-ACO. Ces résultats ne donnent pas un accord parfait compte tenu de la basse « résolution » (2 chiﬀres signiﬁcatifs). $mod ℛ xx$ et $exp ℛ xx$ (resp. $mod ℛyy$ et $exp ℛ yy$ ) sont les valeurs rms en millimètres des matrices-réponse théorique et expérimentale horizontales (resp. verticales). $Δ$ $ℛxx$ et $Δ$ $ℛyy$ donnent l’écart rms entre ces matrices.

En pratique, l’orbite fermée est mesurée sur Super-ACO avec seulement deux chiﬀres signiﬁcatifs. Pour avoir une bonne convergence numérique, les données sont complétées par des zéros pour ces tests. En prenant huit chiﬀres signiﬁcatifs, l’ajustement est parfait, i.e. avec erreur relative de l’ordre de la précision machine (cf. infra).

5.1.3.3 Test complet du modèle

Pour vériﬁer le bon fonctionnement du programme LOCO, on simule des défauts sur les gradients des quadripôles en conservant la symétrie quatre de l’anneau.

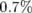Pour commencer, on dérègle le gradient de $Q1$ de $0.7%$ : on observe un glissement des nombres d’ondes : $Δνx=−0.02$ et $Δ νy = 0.03$ .

Au bout de deux itérations, LOCO retrouve exactement les bonnes valeurs des gradients (comparer les valeurs attendues et ﬁnales du tableau 5.2. Les calculs sont faits en simple précision).


	Q1[K1]	Q2[K1]	Q3[K1]	Q4[K1]	$νx$	$νy$

Initiaux	-1.4772282	2.6204337	2.4783405	-1.4238337	4.738429	1.711246
Attendus	-1.4672282	2.6204337	2.4783405	-1.4238337	4.758429	1.708246
Finaux	-1.4672282	2.6204337	2.4783406	-1.4238338	4.758429	1.708246
Ecarts rel.	-2E-8	1E-8	4E-8	-2E-8	3E-8	1E-8

rms	$ℛmxoxd$	$ℛexxxp$	$Δ$ $ℛxx$	$ℛmoydy$	$ℛeyxyp$	$Δ$ $ℛyy$

Initiaux	2.7376	2.8582	0.17748	1.9891	1.8530	0.24700
Finaux	2.8582	2.8582	0.63712E-05	1.8530	1.8530	0.66144E-06

TAB. 5.2:

Ajustement du code LOCO après avoir déréglé le gradient $K1$ de la famille quadripolaire $Q1$ (en symétrie 4). Ecarts relatifs et convergence en prenant 8 chiﬀres signiﬁcatifs dans l’expression de la matrice-réponse. L’ajustement est « parfait ».

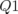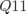Puis, on dérègle de nouveau le gradient de la première famille $Q1$ de $3%$ mais uniquement sur le quadripôle $Q11$ on observe un glissement des nombres d’ondes $Δ ν = − 0.012 x$ et $Δ ν = 0.009 y$ . Encore une fois, le programme LOCO converge en trois itérations vers les valeurs escomptées avec les bons nombres d’ondes (cf. tableau 5.3).


	Q11[K1]	Q12[K1]	Q13[K1]	Q14[K1]	Q15[K1]	Q16[K1]	Q17[K1]	Q18[K1]

$ΔK K$	-1.3E-7	-4.8E-7	-4.0E-7	-4.1E-7	-4.1E-7	-2.1E-7	-2.2E-7	-4.7E-7

	Q21[K1]	Q22[K1]	Q23[K1]	Q24[K1]	Q25[K1]	Q26[K1]	Q27[K1]	Q28[K1]

$ΔKK$	-5.5E-7	-3.8E-7	-4E-8	-3.4E-7	-6.3E-7	-2.5E-7	-2.6E-7	-4.1E-7

	Q31[K1]	Q32[K1]	Q33[K1]	Q34[K1]	Q35[K1]	Q36[K1]	Q37[K1]	Q38[K1]

$ΔK K$	-7.5E-7	-5.3E-7	-4.4E-7	-5E-8	-2.7E-7	-1.25E-7	-2.1E-7	-5.5E-7

	Q41[K1]	Q42[K1]	Q43[K1]	Q44[K1]	Q45[K1]	Q46[K1]	Q47[K1]	Q48[K1]

$ΔK K$	-5.5E-7	-3.5E-7	-1.3E-7	-4.1E-7	-5.5E-7	-3.3E-7	-2.2E-7	-4.8E-7

rms	$mod ℛxx$	$exp ℛ xx$	$Δ$ $ℛxx$	$mod ℛ yy$	$exp ℛ yy$	$Δ$ $ℛyy$	$νx$	$νy$

Finaux	2.8582	2.8582	3.65E-05	1.8530	1.8530	1.39E-06	4.758925	1.706219

TAB. 5.3:

Ajustement du code LOCO après avoir déréglé le gradient $K1$ du premier quadripôle $Q11$ de Super-ACO (la symétrie 4 est brisée). Les écarts relatifs ﬁnaux pour les gradients ( $K1$ ) de 32 quadripôles ( $Qij$ ) correspondent à la précision machine (8 chiﬀres signiﬁcatifs) : le code LOCO retrouve bien le bon modèle de l’anneau.

[prev] [prev-tail] [front] [up]