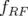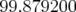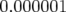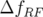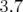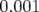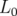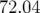5.1.4 Etapes préliminaires à l’analyse des matrices-réponse
Pour utiliser le programme LOCO, il est nécessaire de faire deux mesures supplémentaires :
- une mesure du bruit rms des 16 BPM.
- une mesure de la fonction dispersion dans chaque BPM.
5.1.4.1 Bruit moyen des BPM
Deux jeux de données ont été mesurés :
- 1 000 orbites au début de l’expérience, avec les hexapôles éteints et les onduleurs ouverts.
- 100 orbites en fin d’expériences, hexapôles allumés et les onduleurs fermés.
Les figures 5.3 donnent les résultats moyennés pour chaque BPM  ainsi que les valeurs de bruit
rms,
ainsi que les valeurs de bruit
rms, 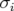 , pour les deux cas considérés. De manière générale, les valeurs de bruits sont plus élevées
en début qu’en fin d’expérience (Tab. 5.4). Le bruit des BPM a également été mesuré le mercredi
20 septembre et mercredi 4 novembre 2000 ; les valeurs rms de bruit dans les deux plans valent
, pour les deux cas considérés. De manière générale, les valeurs de bruits sont plus élevées
en début qu’en fin d’expérience (Tab. 5.4). Le bruit des BPM a également été mesuré le mercredi
20 septembre et mercredi 4 novembre 2000 ; les valeurs rms de bruit dans les deux plans valent
 ,
ce qui correspond à la précision des BPM. Ces valeurs de bruit donnent la limite de convergence
qu’on peut espérer atteindre avec l’algorithme LOCO.
,
ce qui correspond à la précision des BPM. Ces valeurs de bruit donnent la limite de convergence
qu’on peut espérer atteindre avec l’algorithme LOCO.
5.1.4.2 Mesure de la fonction dispersion dans les BPM
La fonction dispersion, 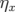 , dans les BPM est calculée avec la formule usuelle (Rice in Chao et
Tigner, 1998) :
, dans les BPM est calculée avec la formule usuelle (Rice in Chao et
Tigner, 1998) :
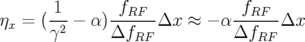 | (5.7) |
avec  , le facteur d’allongement du premier ordre (momentum compaction) et
, le facteur d’allongement du premier ordre (momentum compaction) et 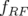 , la
fréquence RF de l’anneau. Pour cela, on réalise deux mesures d’orbite fermée (
, la
fréquence RF de l’anneau. Pour cela, on réalise deux mesures d’orbite fermée ( ), pour deux
fréquences RF distinctes (
), pour deux
fréquences RF distinctes ( ) juste avant l’acquisition de chacune des matrices-réponse (cf.
paramètres Tab. 5.5). L’erreur relative sur la valeur des dispersions est donnée par la formule :
) juste avant l’acquisition de chacune des matrices-réponse (cf.
paramètres Tab. 5.5). L’erreur relative sur la valeur des dispersions est donnée par la formule :
soit en moyenne 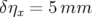 .
.
 ainsi que les valeurs de bruit
rms,
ainsi que les valeurs de bruit
rms, 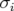 , pour les deux cas considérés. De manière générale, les valeurs de bruits sont plus élevées
en début qu’en fin d’expérience (Tab. 5.4). Le bruit des BPM a également été mesuré le mercredi
20 septembre et mercredi 4 novembre 2000 ; les valeurs rms de bruit dans les deux plans valent
, pour les deux cas considérés. De manière générale, les valeurs de bruits sont plus élevées
en début qu’en fin d’expérience (Tab. 5.4). Le bruit des BPM a également été mesuré le mercredi
20 septembre et mercredi 4 novembre 2000 ; les valeurs rms de bruit dans les deux plans valent
 6,
ce qui correspond à la précision des BPM. Ces valeurs de bruit donnent la limite de convergence
qu’on peut espérer atteindre avec l’algorithme LOCO.
6,
ce qui correspond à la précision des BPM. Ces valeurs de bruit donnent la limite de convergence
qu’on peut espérer atteindre avec l’algorithme LOCO. 
 de Super-ACO dans les plans
vertical et horizontal (précision
de Super-ACO dans les plans
vertical et horizontal (précision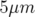 ). Les écarts entre les bruit pour 1 000 et 100 orbites
peuvent s’expliquer par le fait que dans un cas les onduleurs sont fermés et que le courant
stocké est différent.
). Les écarts entre les bruit pour 1 000 et 100 orbites
peuvent s’expliquer par le fait que dans un cas les onduleurs sont fermés et que le courant
stocké est différent. 
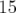
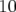
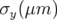


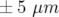 ).
).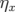 , dans les BPM est calculée avec la formule usuelle (Rice
, dans les BPM est calculée avec la formule usuelle (Rice 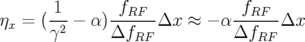
 , le facteur d’allongement du premier ordre (
, le facteur d’allongement du premier ordre (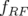 , la
fréquence RF de l’anneau. Pour cela, on réalise deux mesures d’orbite fermée (
, la
fréquence RF de l’anneau. Pour cela, on réalise deux mesures d’orbite fermée ( ), pour deux
fréquences RF distinctes (
), pour deux
fréquences RF distinctes ( ) juste avant l’acquisition de chacune des matrices-réponse (cf.
paramètres Tab.
) juste avant l’acquisition de chacune des matrices-réponse (cf.
paramètres Tab. ![δηx δα δfRF δ ΔfRF δΔx
---- = ---+ ----- + ------- + -----
ηx α fRF ΔfRF Δx
≈ δΔfRF--+ δΔx--
ΔfRF Δx
1
≈ 2.7 × 10− 4 + -------------- (5.8)
Δx [1∕100mm ]](these1941x.png)
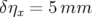 .
.