|
|
Pour chaque kick du perturbateur (aimant dipolaire rapide), on maintient la phase constante par rapport à la synchronisation de référence à des fins de reproductibilité. Les signaux de l’électrode et du perturbateur sont enregistrés tour par tour.
|
|
|
Perturber le faisceau au moyen d’un bump statique ou avec un kick dipolaire correspondent donc à deux réponses très différentes de l’électrode.
 ) où
) où  est le nombre de tours contenant du signal. Pour une transformée de
Fourier rapide (FFT) traditionnelle
est le nombre de tours contenant du signal. Pour une transformée de
Fourier rapide (FFT) traditionnelle 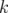 vaut 1 alors que pour l’Analyse en Fréquence
vaut 1 alors que pour l’Analyse en Fréquence 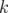 vaut
4.
vaut
4.
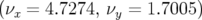 , la variation théorique
des nombres d’ondes est calculée en utilisant le code de calcul MAD version 8
[56].
, la variation théorique
des nombres d’ondes est calculée en utilisant le code de calcul MAD version 8
[56].
|
|
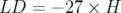
 , sont très différentes des chromaticités
mesurées en particulier dans le plan horizontal (défaut de chromaticité naturelle non
modélisé).
, sont très différentes des chromaticités
mesurées en particulier dans le plan horizontal (défaut de chromaticité naturelle non
modélisé).
 . L’écart peut paraître
faible par rapport au cas précédent, cependant les 4 chiffres significatifs ont toute leur
importance du fait de la précision des mesures en salle de contrôle avec l’oscilloscope
et de la précision de l’Analyse en Fréquence.
. L’écart peut paraître
faible par rapport au cas précédent, cependant les 4 chiffres significatifs ont toute leur
importance du fait de la précision des mesures en salle de contrôle avec l’oscilloscope
et de la précision de l’Analyse en Fréquence.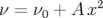 : c’est la première contribution au glissement des nombres d’ondes
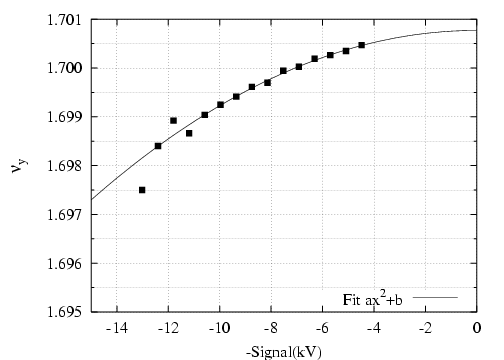
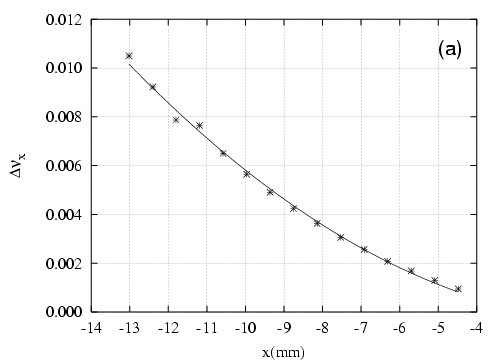
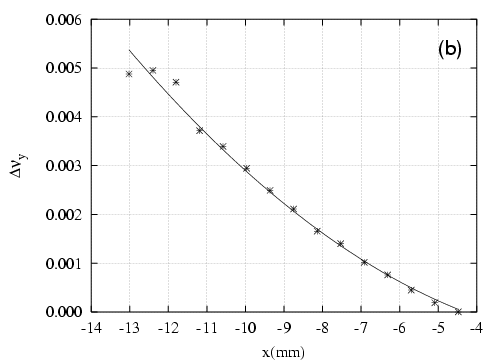
avec l’amplitude (cf. Fig. 5.39)
: c’est la première contribution au glissement des nombres d’ondes
avec l’amplitude (cf. Fig. 5.39)
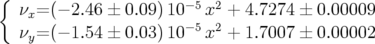 | (5.21) |
Ces résultats permettent de proposer pour la calibration du perturbateur P4, la realtion entre sa tension et l’amplitude imprimée au faisceau :
 | (5.22) |
.
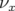 , il semble y avoir vers
, il semble y avoir vers  mm une
perturbation de la dynamique du faisceau — ce n’est pas une erreur sur l’amplitude
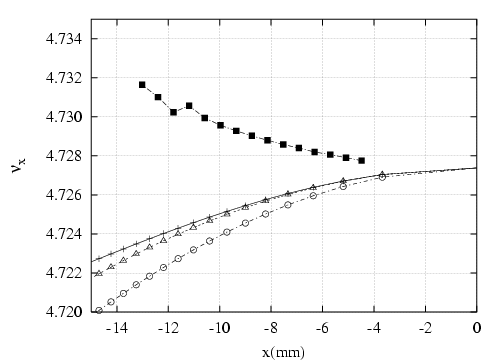
du kick cf. Fig. 5.36, ni a posteriori une résonance car cette irrégularité de la
courbe en fréquence n’est pas observée avec le perturbateur P6 (cf. Fig. 5.45)
—
mm une
perturbation de la dynamique du faisceau — ce n’est pas une erreur sur l’amplitude
du kick cf. Fig. 5.36, ni a posteriori une résonance car cette irrégularité de la
courbe en fréquence n’est pas observée avec le perturbateur P6 (cf. Fig. 5.45)
—
 kV : le bord de l’ouverture
dynamique est atteint.
kV : le bord de l’ouverture
dynamique est atteint.
 est opposée entre la théorie et l’expérience (cf.
Fig. 5.40). Celle de
est opposée entre la théorie et l’expérience (cf.
Fig. 5.40). Celle de 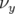 est décroissante avec l’amplitude mais avec une pente beaucoup
plus importante dans le modèle de Super-ACO.
est décroissante avec l’amplitude mais avec une pente beaucoup
plus importante dans le modèle de Super-ACO.
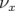 .
.
|
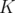 ) des quadripôles et leur
octupôle (
) des quadripôles et leur
octupôle (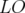 ) lors d’une étude expérimentale de la variation du nombre d’ondes avec
l’énergie de la machine :
) lors d’une étude expérimentale de la variation du nombre d’ondes avec
l’énergie de la machine :
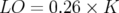 | (5.23) |
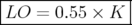 | (5.24) |
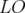 peut
s’écrire :
peut
s’écrire :
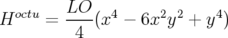 | (5.25) |
Il apparaît immédiatement que pour  petit, l’effet est négligeable sur
petit, l’effet est négligeable sur 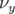 .
.
 pourrait provenir d’un terme hexapolaire (cf. Fig. 5.41) non modélisé.
Cependant l’introduction d’hexapôles tournés ne permet pas d’expliquer cette
différence.
pourrait provenir d’un terme hexapolaire (cf. Fig. 5.41) non modélisé.
Cependant l’introduction d’hexapôles tournés ne permet pas d’expliquer cette
différence.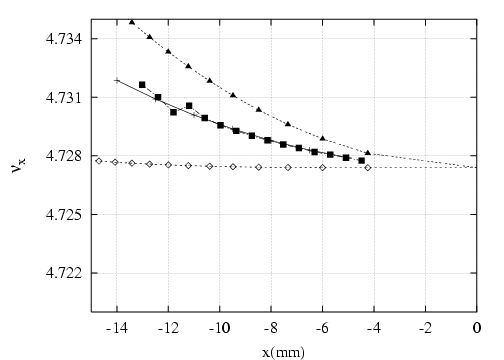 
|
|
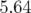 kV (butée basse) à
kV (butée basse) à 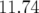 kV (début perte du
faisceau) par pas de 0.5 kV environ.
kV (début perte du
faisceau) par pas de 0.5 kV environ.
![VP 6 ≈ VP 4 + 0.65 [kV ]](these2222x.png) | (5.26) |
|
|
 obtenues après perturbation du
faisceau avec P4 et P6 et après correction des tensions, on observe que les courbes ne
se superposent pas (Fig. 5.45).
obtenues après perturbation du
faisceau avec P4 et P6 et après correction des tensions, on observe que les courbes ne
se superposent pas (Fig. 5.45).
![VP 6 ≈ VP4 + 0.65 + 0.95 [kV ]](these2224x.png) | (5.27) |
|
|
|
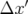 , un phénomène de
décohérence intervient du fait du léger déphasage existant entre chaque particule d’un
paquet. Ce déphasage provient de la dispersion des nombres d’ondes avec l’amplitude,
chaque particule ayant une énergie et une amplitude légèrement différentes des particules
voisines ; si au premier ordre, on écrit :
, un phénomène de
décohérence intervient du fait du léger déphasage existant entre chaque particule d’un
paquet. Ce déphasage provient de la dispersion des nombres d’ondes avec l’amplitude,
chaque particule ayant une énergie et une amplitude légèrement différentes des particules
voisines ; si au premier ordre, on écrit :
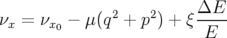 | (5.28) |
avec  et
et  où
où 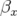 et
et 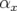 sont les paramètres de Twiss. Si l’on
considère une distribution gaussienne d’écart type
sont les paramètres de Twiss. Si l’on
considère une distribution gaussienne d’écart type 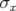 des amplitudes
des amplitudes  et
si l’on néglige le couplage (x-y), l’amortissement, l’excitation quantique et les
interactions entre particules, alors l’évolution du centroïde du faisceau suit la
loi21 :
et
si l’on néglige le couplage (x-y), l’amortissement, l’excitation quantique et les
interactions entre particules, alors l’évolution du centroïde du faisceau suit la
loi21 :
 | (5.29) |
où  est le numéro du tour après le kick d’amplitude
est le numéro du tour après le kick d’amplitude 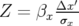 ,
, 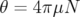 et
et  le facteur chromatique défini par :
le facteur chromatique défini par :
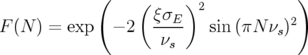 | (5.30) |
avec 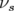 la fréquence synchrotron et
la fréquence synchrotron et  la dispersion en énergie.
la dispersion en énergie.
 , le facteur chromatique
, le facteur chromatique 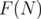 est (
est (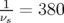 )-tours
périodique).
)-tours
périodique).|
|
Plusieurs constatations sont à faire :
![[− 27, 25] × [− 19, 19]](these2257x.png) mm pour la machine
nominale (i.e. avec toutes les hexapôles allumés). Cette faible valeur s’explique
principalement par les valeurs de chromaticités expérimentales non nulles et ici
élevées dans les deux plans (cf. Tab. 5.18). L’introduction de multipôles (décapôles,
dodécapôles, correcteurs) n’a que peu d’influence sur les dimensions.
mm pour la machine
nominale (i.e. avec toutes les hexapôles allumés). Cette faible valeur s’explique
principalement par les valeurs de chromaticités expérimentales non nulles et ici
élevées dans les deux plans (cf. Tab. 5.18). L’introduction de multipôles (décapôles,
dodécapôles, correcteurs) n’a que peu d’influence sur les dimensions.
![[− 11, 11] × [− 15, 15]](these2258x.png) mm, soit une réduction d’un facteur deux
horizontalement, ce qui est très proche de l’expérience.
mm, soit une réduction d’un facteur deux
horizontalement, ce qui est très proche de l’expérience. avec l’amplitude horizontale est
calculée pour différents modèles de Super-ACO et comparée avec l’expérience (cf.
Fig. 5.50).
avec l’amplitude horizontale est
calculée pour différents modèles de Super-ACO et comparée avec l’expérience (cf.
Fig. 5.50).
 avec l’amplitude
avec l’amplitude
 est inversée lorsque les familles hexapolaires H1 et H2 sont éteintes.
est inversée lorsque les familles hexapolaires H1 et H2 sont éteintes.
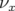 (comparer les courbes avec et
sans octupôles Fig. 5.39 et 5.50) et d’autre part d’expliquer l’inversion du sens de
variation de la courbe en fréquence
(comparer les courbes avec et
sans octupôles Fig. 5.39 et 5.50) et d’autre part d’expliquer l’inversion du sens de
variation de la courbe en fréquence 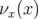 .
.
 )) suffisent
pour retrouver la bonne loi de variation : les hexapôles contribuent donc peu ou prou
à la composante octupolaire.
)) suffisent
pour retrouver la bonne loi de variation : les hexapôles contribuent donc peu ou prou
à la composante octupolaire.
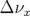 en fonction de l’amplitude (
en fonction de l’amplitude ( ) est très forte :
) est très forte :
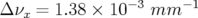 contre
contre  (réglage nominal).
(réglage nominal).
|
|