Aimant dipolaire en coordonnées rectangulaires

A.2.2 Aimant dipolaire en coordonnées rectangulaires

Hamiltonien et description : Il est également possible d’exprimer l’application de transfert en géométrie cartésienne. Le Hamiltonien est alors le même que celui en géométrie curviligne (cf. Eq. A.4) avec $h → 0$ :

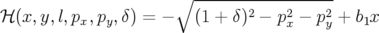∘ ------------------ ℋ (x,y, l,p ,p ,δ ) = − (1 + δ)2 − p2 − p2+ bx x y x y 1

(A.11)

Hypothèse de calcul : La seule hypothèse est l’approximation hard-edge. Le Hamiltonien A.11 est complètement intégrable.

Intégration des équations : L’expression des solutions s’obtient à partie des celles de l’aimant secteur (Eq. A.6 à A.10) en prenant la limite $h → 0$ (Forest, 1994) :

(| (∘ ------------f---------- ∘ ----------------------) ||| xf = xi + 1b1- (1 + δ)2 − (px)2 − (piy)2 − (1 + δ)2 − (pix)2 − (piy)2 ||| |||| pfx = pix − b1s[ ] ||{ f i piy- -----pix----- -----pfx------ y = y + b1 arcsin√ (1+δ)2−-(piy)2 − arcsin √ (1+δ)2−-(piy)2 || f i ||| py = py [ ] ||| f i (1+δ) -----pix----- -----pfx------ |||| l = l + b1 arcsin√ (1+δ)2−(piy)2 − arcsin √(1+δ)2− (piy)2 |( f δ = δ

(A.12)

avec $s=L$ et généralement $b1 = h$ .

[prev] [prev-tail] [front] [up]