Nous avons vu qu’il est difficile de modéliser correctement la dynamique réelle d’un anneau de stockage, car il faut être capable d’identifier les principales résonances pour essayer ensuite de limiter leur influence. Ce travail est délicat si bien que souvent l’écart entre les performances escomptées et réelles pour une machine donnée peut atteindre plus d’un facteur deux. L’Analyse en Fréquence est ici utilisée pour réaliser ce lien entre théorie et expérience.
Dans le chapitre précédent, nous avons calculé des cartes en fréquence de l’ALS considérée soit comme une machine idéale avec sa 12-périodicité, soit comme une machine réelle, i.e. incorporant les défauts magnétiques mesurés. Pour mémoire, les nombres d’ondes choisis correspondent au point de fonctionnement nominal de l’ALS, tout comme les chromaticités qui sont légèrement surcompensées. Les deux cartes en fréquence obtenues (voir figure 4.1) mettent en évidence combien la dynamique est sensible aux défauts magnétiques : leur introduction réduit d’un facteur deux l’extension spatiale de la carte en fréquence, les largeurs de résonances sont plus importantes, de nouvelles droites de résonance apparaissent et la stabilité du faisceau est fortement détériorée. Les performances déduites de ce nouveau modèle sont maintenant beaucoup plus proches de l’expérience. L’ultime étape est désormais de pouvoir comparer notre modélisation de l’ALS directement avec la machine en fonctionnement.
Les résultats que nous avons obtenus s’inscrivent dans une longue collaboration entre J. Laskar et le groupe accélérateur de D. Robin à Berkeley. Une première étude théorique de l’ALS avec l’Analyse en Fréquence a été réalisée dès 1993 (Dumas et Laskar, 1993). Les réglages magnétiques utilisés actuellement sur l’ALS sont très voisins de ceux proposés en 1996 (Laskar et Robin, 1996) et avaient permis d’améliorer significativement les performances machine (temps d’injection du faisceau dans l’anneau, durée de vie). Cependant des écarts encore importants subsistaient entre la théorie et l’expérience. Un long et délicat travail de caractérisation des défauts magnétiques expérimentaux de chaque type d’aimant a été entrepris jusqu’à ce jour.
Cette étape préliminaire est fondamentale et est une condition sine qua non
avant toute tentative d’étude de la dynamique nonlinéaire. Elle a permis d’obtenir
une calibration du modèle linéaire de l’ALS. Pour cela, les matrices-réponse
expérimentales1
sont analysées depuis de nombreuses années (Robin, Safranek et Decking, 1999) en utilisant le
programme LOCO (Safranek, 1997) que nous décrirons dans le chapitre 5. Dans cette analyse, tous
les gradients quadripolaires (naturels et induits dans les hexapôles) sont déterminés avec une
précision d’environ un millième. Après correction, les battements des fonctions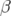 
sont
relativement faibles, 1% et 2% respectivement dans les plans horizontal et vertical. De plus, le
programme LOCO a été récemment modifié pour permettre de modéliser le couplage à
partir des matrices-réponse de l’anneau en un temps de calcul non prohibitif (Steier,
2000).
Les questions que l’on se pose actuellement sont : quelle fiabilité accorder à ce modèle de
l’anneau ? Que se passe-t-il si nous modifions l’optique de la machine ? Quel est l’impact des
sections à faible fonction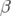 
(low beta insertion straight sections), l’impact de l’introduction de
nouveaux éléments ? Par exemple, au mois d’août 2001, trois des trente-six dipôles (à 1.3 Tesla) de
l’ALS seront remplacés par des aimants supraconducteurs (à 5 Tesla). Comment améliorer les
performances de l’anneau aujourd’hui ?
(
et
). Les défauts des quadripôles droits et tournés déduits des matrices-réponse
expérimentales brisent la symétrie 12 de l’anneau