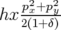 dit des petites machines ne peut plus être négligé. En particulier, il
doit être pris en compte pour les calculs de chromaticité. Le Hamiltonien d’un dipôle simple est
obtenu à partir des équations 1.36 et 1.51 :
dit des petites machines ne peut plus être négligé. En particulier, il
doit être pris en compte pour les calculs de chromaticité. Le Hamiltonien d’un dipôle simple est
obtenu à partir des équations 1.36 et 1.51 :
Description et Hamiltonien : Pour les machines à faible rayon de courbure comme Super-ACO,
le terme hexapolaire 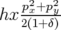 dit des petites machines ne peut plus être négligé. En particulier, il
doit être pris en compte pour les calculs de chromaticité. Le Hamiltonien d’un dipôle simple est
obtenu à partir des équations 1.36 et 1.51 :
dit des petites machines ne peut plus être négligé. En particulier, il
doit être pris en compte pour les calculs de chromaticité. Le Hamiltonien d’un dipôle simple est
obtenu à partir des équations 1.36 et 1.51 :
 |
Je vais maintenant présenter un schéma d’intégration symplectique avec correcteur.
Hypothèses de calcul : (a) l’approximation des petits angles et (b) hard-edge sont réalisées pour établir cet Hamiltonien.
Les équations du mouvement se réduisent à (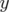 et
et  sont cycliques) :
sont cycliques) :
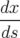 | = (1 + hx)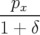 | 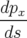 | = −h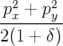 + hδ + hδ | (A.24a) |
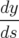 | = (1 + hx)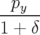 |  | = 0 | (A.24b) |
 | = −(1 + hx) − hx − hx |  | = 0 | (A.24c) |
On a immédiatement  , puis pour
, puis pour  (Eq. A.24a) :
(Eq. A.24a) :
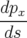 | = −h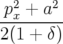 avec a2 = (p
yi)2 − 2(1 + δ)δ > 0 avec a2 = (p
yi)2 − 2(1 + δ)δ > 0 | ||
| ∫ |  = ∫
− = ∫
−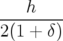 ds ds | ||
| en utilisant la primitive usuelle : | |||
∫
 | =  arctan arctan  + + 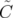 , , 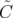 ∈ ℝ ∈ ℝ | ||
| on a alors : | |||
arctan  | = arctan  − − s s | ||
| en utilisant : | |||
| tan(a + b) | =  , , | ||
| on obtient : | |||
pxf = a![[pix − atan θ]
-----i------
a + pxtan θ](these2581x.png) | (A.25) | ||
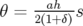 et
et  .
.
L’équation A.24a pour  peut être maintenant intégrée :
peut être maintenant intégrée :
![|-------------------------------------------------------------------|
| ( ( i)2 ) [ ( i )] |
yf = yi + 1 + px- (h−1 + xi) θ − sin θcos θ − 2arctan px- |
| a a |
---------------------------------------------------------------------](these2593x.png) | (A.27) |
Dans le cas 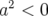 , les équations A.25 à A.27 deviennent :
, les équations A.25 à A.27 deviennent :
| |1 + hxf | | = ![{ |1 + hxi|--C+---(u++1-)2- si p ∈] − |a|,|a|[
(1+C+− )2 −u+ 2 x
|1 + hxi|(1−CC−)2 (u-u−−1) si px ⁄∈] − |a|,|a|[](these2595x.png) | (A.28) |
| px f | = ![{ +
a u1+u−+1- si px ∈ ] − |a|,|a|[
a 1+u-−- si p ⁄∈ ] − |a|,|a |[
u−1− x](these2596x.png) | (A.29) |
| yf | = ![( [ ]
{ yi + piy|1 + hxi|--C++-2 u+ − C+ − 1+ + -1+-+ 2 ln |u++-| si px ∈] − |a|,|a|[
ahi (1+C− ) [ u C C− ]
( yi + payh|1 + hxi|(1−CC−)2 u− − C− − 1u−-+ C1−-− 2 ln|uC−-| si px ⁄∈ ] − |a|,|a|[](these2597x.png) | (A.30) |
 ,
,  ,
, 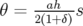 et
et  .
.
Il n’y a qu’une seule équation à intégrer, car toutes les autres variables canoniques sont des constantes du mouvement :
 | (A.31) |
Le calcul du correcteur est relativement aisé, il s’exprime par :
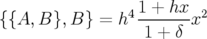 | (A.32) |
On obtient alors l’application recherchée :
 | (A.33) |