[prev] [prev-tail] [tail] [up]

A.2.5 Dipôle droit en coordonnées rectangulaires

Hamiltonien : son expression est obtenue en posant h = 0 dans le Hamiltonien 1.36 :

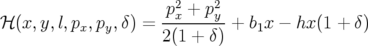2 2 ℋ (x,y,l,p ,p ,δ) = -px +-py + b x − hx (1 + δ) x y 2(1 + δ) 1
(A.21)

avec b1 la force dipolaire.

( ( |{ dxds- = 1p+xδ |{ ddpsx = − (b1 − h(1 + δ)) dy- = -py dpy |( ds 1+pδ2+p2 |( ds = 0 ddsl = 2(x1+δy)2 + hx ddδs = 0
(A.22)

Hypothèses de calcul : Les approximations (a) des grandes machines, (b) des petits angles et (c) hard-edge ont été faites pour établir l’expression A.22 qui est complètement intégrable.

Application de transfert : L’intégration des équations du mouvement est immédiate :

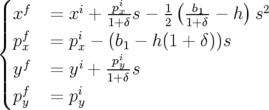( f i pix 1(b1 ) 2 ||| x = x + 1+-δs − 2 1+-δ − h s |{ pfx = pix − (b1 − h(1 + δ))s f i piy ||| y = y + 1+-δs |( pf = pi y y
(A.23)

[prev] [prev-tail] [front] [up]