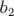 , de courbure
, de courbure 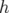 et de longueur
et de longueur 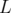 . Son Hamiltonien développé à l’ordre
deux en les impulsions est (cf. Eq. 2.41) :
. Son Hamiltonien développé à l’ordre
deux en les impulsions est (cf. Eq. 2.41) :
Description et Hamiltonien : Dans cette partie, nous considérons un dipôle combiné de
gradient quadripolaire 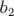 , de courbure
, de courbure 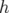 et de longueur
et de longueur 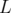 . Son Hamiltonien développé à l’ordre
deux en les impulsions est (cf. Eq. 2.41) :
. Son Hamiltonien développé à l’ordre
deux en les impulsions est (cf. Eq. 2.41) :
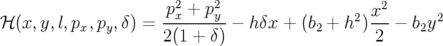 | (A.15) |
Les équations du mouvement (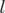 est cyclique) :
est cyclique) :
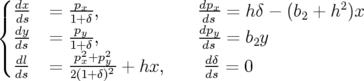 | (A.16) |
Hypothèses de calcul : Les approximations (a) des grandes machines, (b) des petits angles et (c) hard-edge ont été faites pour établir l’expression A.15 qui est complètement intégrable.
Application de transfert : Si l’on ne considère que les équations horizontales, on obtient une équation différentielle du second ordre de type oscillateur harmonique :
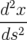 | = 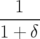 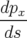 = = 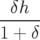 − −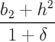 x x | ||
| alors : | |||
| xf | =  | (A.17) | |
avec ωx+ =  et ωx− = et ωx− = 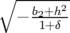 | |||
| px f | = 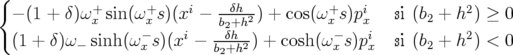 | (A.18) | |
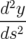 | = 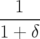 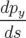 = = 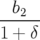 y y | ||
| alors : | |||
| yf | = 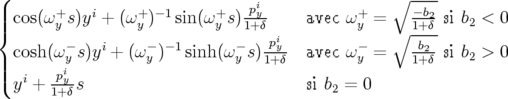 | (A.19) | |
| et : | |||
| pyf | = 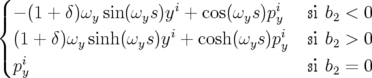 | (A.20) | |