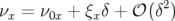
Considérons une particule animée d’un mouvement bétatron (cf. chap. 1, Eq. 1.60). La variation du nombre d’ondes horizontal dépend de l’énergie de la particule à travers la chromaticité :
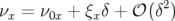 | (4.2) |
où  est la fonction chromaticité et
est la fonction chromaticité et 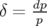 l’écart à l’énergie
nominale4.
l’écart à l’énergie
nominale4.
Si l’on appelle 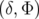 ses coordonnées
canoniques5
dans l’espace des phases longitudinal, alors dans l’approximation linéaire, la dynamique
longitudinale est gouvernée par le Hamiltonien (voir par exemple Lee, 1998) :
ses coordonnées
canoniques5
dans l’espace des phases longitudinal, alors dans l’approximation linéaire, la dynamique
longitudinale est gouvernée par le Hamiltonien (voir par exemple Lee, 1998) :
| H | =  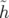 w0ηcδ2 − w0ηcδ2 −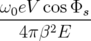 Φ2 Φ2 | ||
=  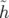 w0ηcδ2 + w0ηcδ2 +   Φ2 Φ2 | (4.3) |
 la fréquence synchrotron,
la fréquence synchrotron,  la fréquence de révolution,
la fréquence de révolution, 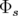 la
phase synchrone,
la
phase synchrone,  la tension radiofréquence effective,
la tension radiofréquence effective, 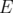 l’énergie de la particule,
l’énergie de la particule,
 ,
,  le nombre d’harmoniques et
le nombre d’harmoniques et 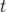 la variable indépendante.
la variable indépendante.
La trajectoire de phase est une ellipse d’équation dont nous choisissons d’écrire le paramétrage sous la forme :
 | (4.4) |
avec 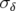 et
et  les dimensions d’équilibre des variables
les dimensions d’équilibre des variables 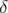 et
et 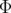 et
et  , l’aire de
l’ellipse de phase. Le glissement de la fréquence bétatron mesuré au n-ième tour s’écrit (Eq. 4.2 et
4.4) :
, l’aire de
l’ellipse de phase. Le glissement de la fréquence bétatron mesuré au n-ième tour s’écrit (Eq. 4.2 et
4.4) :
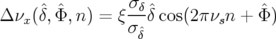 | (4.5) |
et le déphasage induit sur  tours pour la particule considérée est par définition :
tours pour la particule considérée est par définition :
Δφx(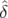 , ,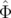 ,n) ,n) | = 2π ∫
0nΔν
x(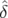 , ,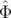 ,k) dk ,k) dk | ||
| soit en utilisant l’expression 4.5 : | |||
Δφx(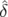 , , ,n) ,n) | = ξ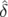  νs−1(sin(2πν
sn + νs−1(sin(2πν
sn + 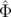 ) − sin( ) − sin(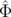 )) )) | ||
= ![[ ]
2ξν−s1σδ sin(π νsn)](these1629x.png)  cos(πνsn + cos(πνsn +  ) ) | |||
= 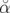  cos(πνsn + cos(πνsn +  ) avec ) avec 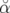 = = ![[ − 1 ]
2ξνs σδ sin(πνsn)](these1636x.png) | |||
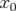 obéit à la
loi :
obéit à la
loi :
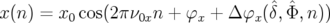 | (4.6) |
Le mouvement du centroïde d’un paquet de particules distribuées en
amplitude et phase selon une densité de probabilités 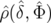 s’exprime alors
comme6 :
s’exprime alors
comme6 :
 | (4.7) |
Si les lois de distribution en amplitudes 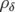 et en phases
et en phases  des particules sont des gaussiennes de
moyennes nulles et d’écart-types respectifs
des particules sont des gaussiennes de
moyennes nulles et d’écart-types respectifs 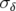 et
et 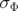 , alors la fonction de densité de probabilité
conjointe est :
, alors la fonction de densité de probabilité
conjointe est :
| ρ(δ, Φ) | = ρδ(δ)ρΦ(Φ) | ||
= 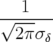 e− e−
 e− e−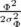
| |||
=  e− e−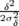 − −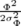
| (4.8) |
La fonction densité de probabilité  dans les nouvelles variables amplitude-phase
dans les nouvelles variables amplitude-phase  se
déduit immédiatement (Eq. 4.4 et 4.8) :
se
déduit immédiatement (Eq. 4.4 et 4.8) :
 | (4.9) |
où  est le jacobien de la transformation continue de coordonnées 4.4 :
est le jacobien de la transformation continue de coordonnées 4.4 : 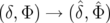 .
.
Le mouvement du centroïde (Eq. 4.7) devient en utilisant l’équation 4.9 :
 | (4.15) |
Le centroïde du faisceau effectue des oscillations bétatrons modulées par le facteur chromatique
 . Ce dernier est une fonction
. Ce dernier est une fonction  -périodique dont les extrema
sont
-périodique dont les extrema
sont 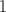 et
et 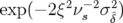 . Au premier ordre, la fréquence d’oscillation du centroïde n’est pas
modifiée, car la distribution des phases bétatrons est symétrique par rapport à la phase
synchrone.
. Au premier ordre, la fréquence d’oscillation du centroïde n’est pas
modifiée, car la distribution des phases bétatrons est symétrique par rapport à la phase
synchrone.