 BPM,
BPM, 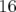 correcteurs horizontaux et 16 correcteurs verticaux, donc la
matrice-réponse non couplée a
correcteurs horizontaux et 16 correcteurs verticaux, donc la
matrice-réponse non couplée a 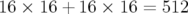 éléments.
éléments.
On dispose de  BPM,
BPM, 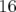 correcteurs horizontaux et 16 correcteurs verticaux, donc la
matrice-réponse non couplée a
correcteurs horizontaux et 16 correcteurs verticaux, donc la
matrice-réponse non couplée a 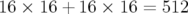 éléments.
éléments.
Pour générer les matrices-réponse, on allume successivement les correcteurs avec un courant de  , soit
approximativement
, soit
approximativement 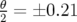 mrad pour un correcteur horizontal et
mrad pour un correcteur horizontal et  mrad pour un correcteur
vertical7,
et on mesure dans chaque BPM le déplacement de l’orbite fermée.
mrad pour un correcteur
vertical7,
et on mesure dans chaque BPM le déplacement de l’orbite fermée.
L’ajustement entre matrices expérimentale et modèle est réalisé en faisant varier les forces quadripolaires soit en familles (4), soit individuellement (32), les gains des correcteurs horizontaux (16) et verticaux (16), les gains des BPM horizontaux (16) et verticaux (16). Pour finir, dans les sections dispersives, le déplacement supplémentaire de l’orbite associé au glissement en énergie est pris en compte (parfois appelé facteur d’Amman [Amman, 1971]),
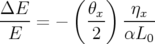 | (5.9) |
avec  le facteur d’allongement du premier ordre et
le facteur d’allongement du premier ordre et  la circonférence de la machine.
la circonférence de la machine.
En effet, la déviation 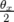 produite par le correcteur dipolaire engendre — si la fonction
dispersion
produite par le correcteur dipolaire engendre — si la fonction
dispersion 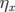 est non nulle — une modification de la longueur
est non nulle — une modification de la longueur 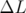 de l’orbite de la
particule :
de l’orbite de la
particule :
 | (5.10) |
allongement équivalent à une modification de l’énergie de la particule :
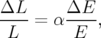 | (5.11) |
ce qui ajoute 16 nouveaux paramètres8. Au total, l’ajustement est réalisé sur 84 (ou 112) paramètres.
Cependant, on ne peut pas faire varier de manière indépendante l’ensemble des gains des BPM et des correcteurs sous peine de dégénérescence. En effet, si tous les gains des BPM sont augmentés d’un même facteur alors que ceux des correcteurs sont diminués proportionnellement alors la matrice-réponse reste inchangée : la SVD donne deux valeurs propres nulles. Pour lever cette dégénérescence, il suffit de fixer par exemple le gain d’un correcteur horizontal et d’un correcteur vertical.
Pour l’optique de Super-ACO utilisée, le courant stocké était de  mA dans 24 paquets, en
faisceau « plat »
mA dans 24 paquets, en
faisceau « plat »  , ceci avec les quatre familles d’hexapôles éteintes.
Cette possibilité d’éteindre les hexapôles avec un faisceau circulant dans l’anneau est un
avantage qui permettra de déterminer les défauts de gradients indépendamment de ceux
induits par les hexapôles lorsqu’il existe une orbite résiduelle
, ceci avec les quatre familles d’hexapôles éteintes.
Cette possibilité d’éteindre les hexapôles avec un faisceau circulant dans l’anneau est un
avantage qui permettra de déterminer les défauts de gradients indépendamment de ceux
induits par les hexapôles lorsqu’il existe une orbite résiduelle 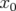 en leur centre (cf.
section 5.1.6).
en leur centre (cf.
section 5.1.6).
|
|
Le modèle utilisé est déduit des mesures de courant dans les
quadripôles9 :
c’est notre modèle de référence de Super-ACO (cf. Tab 5.6). Le point de fonctionnement
théorique devient alors  . Notons que par rapport au point de
fonctionnement nominal, le courant dans
. Notons que par rapport au point de
fonctionnement nominal, le courant dans  ayant changé, les valeurs de la fonction dispersion
théorique sont également légèrement modifiées. Les nombres d’ondes mesurés valent :
ayant changé, les valeurs de la fonction dispersion
théorique sont également légèrement modifiées. Les nombres d’ondes mesurés valent :
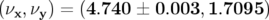 . L’incertitude sur
. L’incertitude sur  provient de la faible valeur du courant
provient de la faible valeur du courant
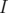 (à l’oscilloscope au lieu d’un pic unique, on en observe plusieurs).
(à l’oscilloscope au lieu d’un pic unique, on en observe plusieurs).
Les résultats sont résumés par la figure 5.4 et le tableau 5.7.
 mm ; l’écart modèle/expérience est
grand, en moyenne de 130%.
mm ; l’écart modèle/expérience est
grand, en moyenne de 130%.
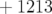 mm ; l’écart modèle/expérience est en
moyenne de 5%.
mm ; l’écart modèle/expérience est en
moyenne de 5%.|
|
|
|
La principale raison de ces écarts est la création d’orbite fermée par les défauts de champs
quadripolaires 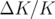 (cf. sous-section 5.1.5.4) suivant la loi (Nadji, 1992).
(cf. sous-section 5.1.5.4) suivant la loi (Nadji, 1992).
En utilisant les résultats de la section suivante, la formule 5.12 donne comme écart moyen sur la
dispersion  mm rms alors que la valeur issue des mesures expérimentales est presque
trois fois plus grande
mm rms alors que la valeur issue des mesures expérimentales est presque
trois fois plus grande 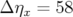 mm rms.
mm rms.
Ajustement sur quatre familles :
Avant l’ajustement, le désaccord entre les orbites mesurées et théoriques est supérieur en valeurs
rms à 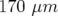 horizontalement (H) et à
horizontalement (H) et à 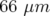 verticalement (V).
verticalement (V).
Après un ajustement sur les quatre familles de quadripôle l’accord est de  (réduction
d’un facteur 5) et
(réduction
d’un facteur 5) et 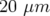 (réduction d’un facteur 3) respectivement dans les plans horizontal et
vertical avec un
(réduction d’un facteur 3) respectivement dans les plans horizontal et
vertical avec un  de 2 080. En suivant les résultats énoncés précédemment, la valeur escomptée
du
de 2 080. En suivant les résultats énoncés précédemment, la valeur escomptée
du 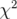 devrait être idéalement au mieux
devrait être idéalement au mieux 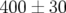 , sachant qu’il y a (
, sachant qu’il y a ( ) points de donnée
et (
) points de donnée
et ( ) paramètres indépendants ajustés. Le point de fonctionnement devient alors
) paramètres indépendants ajustés. Le point de fonctionnement devient alors
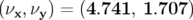 soit
soit  , ce qui est en excellent accord avec
la mesure expérimentale des nombres d’ondes. Les gradients des familles de quadripôles ont varié
de moins de
, ce qui est en excellent accord avec
la mesure expérimentale des nombres d’ondes. Les gradients des familles de quadripôles ont varié
de moins de 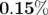 (cf. Tab. 5.8, Fig. 5.5). Il faut remarquer que les écarts relatifs
obtenus pour les gradients sont tous négatifs : ceci ne peut pas être dû à un phénomène
aléatoire.
(cf. Tab. 5.8, Fig. 5.5). Il faut remarquer que les écarts relatifs
obtenus pour les gradients sont tous négatifs : ceci ne peut pas être dû à un phénomène
aléatoire.
|
Les nouvelles fonctions  sont tracées sur la figure 5.6 ; le battement (Fig. 5.7) de la fonction
sont tracées sur la figure 5.6 ; le battement (Fig. 5.7) de la fonction
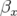 est de
est de  autour de
autour de 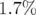 (traduit le glissement
(traduit le glissement  ) et celui de
) et celui de 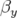 est de
est de
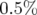 autour de
autour de  (
(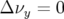 ).
).
Les bruits et gains des BPM ainsi que ceux des correcteurs sont donnés par la figure 5.8. Les
valeurs sont raisonnables ; en moyenne, on retrouve la bonne valeur de kick dipolaire vertical
 . Par contre dans le plan horizontal, la valeur attendue
. Par contre dans le plan horizontal, la valeur attendue 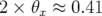 , n’est pas
atteinte dans les régions dispersives. Cet écart est à corréler avec l’écart en dispersion donné par
LOCO (cf. Fig. 5.4).
, n’est pas
atteinte dans les régions dispersives. Cet écart est à corréler avec l’écart en dispersion donné par
LOCO (cf. Fig. 5.4).
|
|
Ajustement sur les quadripôles individuels :
Lorsque l’ajustement est réalisé sur les 32 gradients des quadripôles, la symétrie 4 de l’anneau
est brisée. La convergence semble meilleure : 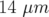 et
et 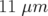 , horizontalement et verticalement
avec comme nombres d’ondes
, horizontalement et verticalement
avec comme nombres d’ondes 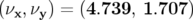 et un
et un  de
de 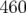 . Les gradients des
quadripôles ont varié de façon plus significative jusqu’à
. Les gradients des
quadripôles ont varié de façon plus significative jusqu’à  (Fig. 5.9). Cependant, cette
variation ne semble pas aléatoire comme l’on s’y attendrait ; bien au contraire, il semble que la
variation sur un quadripôle est rattrapée immédiatement sur le quadripôle suivant. Néanmoins, les
variations en moyenne pour chaque famille correspondent à celles trouvées en symétrie 4.
(Fig. 5.9). Cependant, cette
variation ne semble pas aléatoire comme l’on s’y attendrait ; bien au contraire, il semble que la
variation sur un quadripôle est rattrapée immédiatement sur le quadripôle suivant. Néanmoins, les
variations en moyenne pour chaque famille correspondent à celles trouvées en symétrie 4.
|
|
Ces résultats sont assez surprenants. En effet, briser la symétrie 4 de l’anneau devrait
simplement se traduire par une distribution aléatoire des gradients quadripolaires autour
des valeurs trouvées précédemment pour chaque famille. En aucun cas, la justification
de variation de l’ordre du pourcentage ne semble plausible, ce qui est bien au-delà des
valeurs provenant des mesures magnétiques (Barthès et al., 1990, voir Fig. 3.22, p. §). De
plus, une aussi faible valeur du 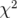 suggère, ou bien que la machine est parfaitement
connue, ou bien que le nombre de paramètres ajustés est trop important. La dernière
hypothèse semble la plus raisonnable : nous essayons d’ajuster 32 valeurs de gradients en
utilisant les mesures de 16 BPM à quatre électrodes. Les autres paramètres, les gains des
correcteurs et des BPM et les facteurs d’Amman, peuvent être vus comme de poids secondaire
dans l’ajustement. Le même type de problème est par exemple rencontré à l’ALS où il y
a 104 gradients quadripolaires à ajuster sur 96 BPM (communication personnelle, C.
Steier).
suggère, ou bien que la machine est parfaitement
connue, ou bien que le nombre de paramètres ajustés est trop important. La dernière
hypothèse semble la plus raisonnable : nous essayons d’ajuster 32 valeurs de gradients en
utilisant les mesures de 16 BPM à quatre électrodes. Les autres paramètres, les gains des
correcteurs et des BPM et les facteurs d’Amman, peuvent être vus comme de poids secondaire
dans l’ajustement. Le même type de problème est par exemple rencontré à l’ALS où il y
a 104 gradients quadripolaires à ajuster sur 96 BPM (communication personnelle, C.
Steier).
Nous voudrions connaître, parmi ces 104 paramètres, combien ont une influence réelle
sur l’ajustement. La réponse à cette question est fournie par l’analyse du spectre des
valeurs propres résultant de la décomposition en valeurs singulières. Sur la figure 5.10, les
valeurs propres (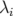 ) sont rangées par ordre décroissant de l’amplitude. On observe une
décroissance rapide des amplitudes avec deux seuils : le premier en
) sont rangées par ordre décroissant de l’amplitude. On observe une
décroissance rapide des amplitudes avec deux seuils : le premier en  , le second en
, le second en 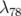 .
.
|
|
Ces résultats suggèrent de réaliser l’ajustement en rejetant tous les paramètres conduisant à des
valeurs propres inférieures au seuil 1 ou 2. Il s’avère que ne rejeter que les valeurs propres plus petites que le
seuil 2 n’améliore pas les résultats précédents. Comme attendu à la lecture du spectre, seul le seuil 1 est
significatif10 :
la convergence est maintenant de  (H) et
(H) et 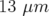 (V) avec comme nouveaux nombres
d’ondes
(V) avec comme nouveaux nombres
d’ondes 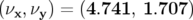 et un
et un 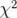 plus élevé de 1 050. La variation des gradients
individuels est aléatoire et avec des amplitudes très voisines de celles obtenues pour les familles de
quadripôles (Fig. 5.11).
plus élevé de 1 050. La variation des gradients
individuels est aléatoire et avec des amplitudes très voisines de celles obtenues pour les familles de
quadripôles (Fig. 5.11).
|
|
La convergence est acceptable si l’on considère la valeur moyenne du bruit des BPM, sachant que de toute manière les mesures ne sont faites avec seulement deux chiffres significatifs, i.e. une bien faible résolution inhérente à Super-ACO.
A titre indicatif, la figure 5.12 illustre les variations relatives des gradients par rapport aux valeurs déduites de l’ajustement en familles.
|
|
Les nouvelles fonctions  sont tracées sur la figure 5.13. et leurs battements sur la figure 5.14.
Les battements,
sont tracées sur la figure 5.13. et leurs battements sur la figure 5.14.
Les battements, 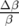 , sont plus importants horizontalement (
, sont plus importants horizontalement (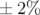 autour de
autour de 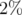 ) que
verticalement
) que
verticalement  . Ils s’expriment en première approximation suivant la formule classique
(Rice et Cornell in Chao et Tigner, 1998) :
. Ils s’expriment en première approximation suivant la formule classique
(Rice et Cornell in Chao et Tigner, 1998) :
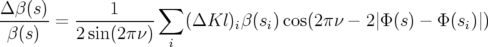 | (5.13) |
où 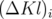 est le gradient intégré du i-ème quadripôle,
est le gradient intégré du i-ème quadripôle,  son avance de phase.
son avance de phase.
Soit avec une formule statistique (Nadji, 1992) :
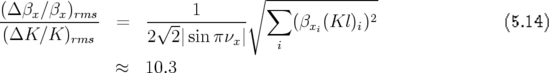
 , ce qui est en accord
avec la figure 5.14.
, ce qui est en accord
avec la figure 5.14.
On remarque que le battement des fonctions d’ondes est maximum pour un déphasage
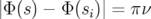 soit pour un défaut dans un quadripôle situé de manière diamétralement
opposée à la position
soit pour un défaut dans un quadripôle situé de manière diamétralement
opposée à la position  du BPM où il est observé.
du BPM où il est observé.
Enfin, LOCO réalisant un ajustement sur le glissement en énergie induit dans les régions dispersives, on peut en déduire les valeurs des dispersions dans les correcteurs, celles dans les BPM ont déjà été mesurées (cf. Eq. 5.9). L’ensemble des résultats en comparaison avec les dispersions déduites de l’ajustement est illustré par la figure 5.15 : l’accord est correct dans les BPM compte tenu des erreurs de mesure. Cependant, il faut noter des écarts dans les correcteurs entre la dispersion déduite du facteur d’Amman et celle donnée par le modèle ajusté. De plus, la dépendance en énergie de la matrice-réponse est traitée trop simplement dans le code LOCO (communication personnelle, H. Zyngier).
La figure 5.16 donne les nouveaux gains des BPM ainsi que le niveau de bruit de chaque BPM et
correcteur et également la valeur ajustée du kick. On remarquera qu’à la convergence, le bruit rms
du BPM  rapporté au bruit total rms de tous les BPM n’est pas voisin de l’unité comme il
devrait l’être théoriquement pour une convergence atteignant le niveau de bruit des
BPM.
rapporté au bruit total rms de tous les BPM n’est pas voisin de l’unité comme il
devrait l’être théoriquement pour une convergence atteignant le niveau de bruit des
BPM.
En conclusion, l’algorithme LOCO ajuste correctement les fonctions 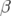 , les nombres d’ondes.
Les défauts de gradients trouvés sont relativement faibles, ce qui suggère un assez bon accord entre
la théorie et l’expérience.
, les nombres d’ondes.
Les défauts de gradients trouvés sont relativement faibles, ce qui suggère un assez bon accord entre
la théorie et l’expérience.
|
|
|
|
|
|