 :
:  .
.
Super-ACO est considéré comme machine parfaite, i.e. sans défauts avec sa 4-périodicité. Les
onduleurs ou wigglers ne sont pas modélisés et de plus les forces des lentilles décapolaires sont
surestimées17
d’un facteur  :
:  .
.
Le point de fonctionnement a pour nombres d’ondes  et
et 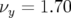 et les hexapôles
chromatiques sont ajustés pour une chromaticité nulle dans les deux plans (tableau 3.5). L’ensemble
des calculs est réalisé pour des particules d’énergie nominale (
et les hexapôles
chromatiques sont ajustés pour une chromaticité nulle dans les deux plans (tableau 3.5). L’ensemble
des calculs est réalisé pour des particules d’énergie nominale ( ). Les fonctions optiques pour
une super-période sont données par la figure 3.17.
). Les fonctions optiques pour
une super-période sont données par la figure 3.17.
|
Les calculs effectués avec le logiciel BETA diffèrent de ceux du logiciel MAD tout particulièrement pour des intégrations à grandes amplitudes. Nous l’avons déjà vérifié dans la section précédente. Les courbes de glissement des nombres d’ondes (Fig. 3.18) sont obtenues en utilisant l’intégrateur LIE4 de MAD.
Il est intéressant de comparer les ouvertures dynamiques calculées avec le logiciel BETA et avec
le code MAD (Fig. 3.19). La méthode de calcul de l’ouverture dynamique de BETA et celle
présentée avec MAD sont radicalement différentes. La philosophie de BETA est de ne tracer que le
bord de l’ouverture dynamique selon le schéma suivant. On se donne une amplitude  à
à
 fixé, on commence l’intégration, si l’on est stable (resp. instable), on incrémente
(resp. décrémente)
fixé, on commence l’intégration, si l’on est stable (resp. instable), on incrémente
(resp. décrémente) 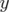 jusqu’à être instable (resp. stable). Ensuite,
jusqu’à être instable (resp. stable). Ensuite,  est incrémenté et
l’on réitère le processus précédent. Notons que par cette méthode, on n’explore pas
l’intérieur de l’ouverture dynamique qui peut alors contenir des régions conduisant à des
mouvements instables. Un des points forts de cette méthode est la rapidité du temps de calcul
qui permet de l’utiliser pour l’optimisation d’une machine pour un faible nombre de
tours.
est incrémenté et
l’on réitère le processus précédent. Notons que par cette méthode, on n’explore pas
l’intérieur de l’ouverture dynamique qui peut alors contenir des régions conduisant à des
mouvements instables. Un des points forts de cette méthode est la rapidité du temps de calcul
qui permet de l’utiliser pour l’optimisation d’une machine pour un faible nombre de
tours.
|
|
Dans le second cas, on n’utilise MAD que pour réaliser l’intégration numérique de la trajectoire.
On se donne une grille de conditions initiales 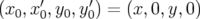 et pour chaque nœud du
maillage, on effectue l’intégration et l’on ne garde que les conditions initiales qui ont conduit à un
mouvement stable. Ce type de calcul est beaucoup plus long, mais il est exhaustif au sens où l’on est
assuré de ne pas avoir de région instable contenue dans l’ouverture dynamique, pourvu que le
maillage soit assez fin (typiquement 150
et pour chaque nœud du
maillage, on effectue l’intégration et l’on ne garde que les conditions initiales qui ont conduit à un
mouvement stable. Ce type de calcul est beaucoup plus long, mais il est exhaustif au sens où l’on est
assuré de ne pas avoir de région instable contenue dans l’ouverture dynamique, pourvu que le
maillage soit assez fin (typiquement 150 150 conditions initiales avec un pas suivant une loi en
racine carrée).
150 conditions initiales avec un pas suivant une loi en
racine carrée).
Dans la présente étude, cette méthode donne des résultats peu différents qualitativement mais complètement différents quantitativement (bijection entre ouverture dynamique et carte en fréquence, localisation des résonances, stabilité).
L’ouverture dynamique (figure 3.20-d) et la carte en fréquence (figure 3.20-c) ont été calculées en
intégrant la trajectoire de 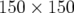 conditions initiales réparties dans le premier quadrant
(
conditions initiales réparties dans le premier quadrant
( ) de l’espace des configurations
) de l’espace des configurations ![(x,y) ∈ [0,50] × [0,60] mm](these1183x.png) . L’intégration est
effectuée sur deux fois 1 000 tours. Les 1 000 premiers tours sont utilisés pour calculer
les fréquences associées au mouvement d’une particule survivante et les 1 000 suivants
pour calculer la diffusion de l’orbite. Ce choix n’est pas arbitraire mais est justifié par
une rapide convergence de l’application fréquence. Rappelons que, grâce aux propriétés
de l’Analyse en Fréquence, l’on est dispensé de réaliser une intégration numérique des
trajectoires pour un nombre de tours de 75 000 correspondant au temps d’amortissement de
Super-ACO.
. L’intégration est
effectuée sur deux fois 1 000 tours. Les 1 000 premiers tours sont utilisés pour calculer
les fréquences associées au mouvement d’une particule survivante et les 1 000 suivants
pour calculer la diffusion de l’orbite. Ce choix n’est pas arbitraire mais est justifié par
une rapide convergence de l’application fréquence. Rappelons que, grâce aux propriétés
de l’Analyse en Fréquence, l’on est dispensé de réaliser une intégration numérique des
trajectoires pour un nombre de tours de 75 000 correspondant au temps d’amortissement de
Super-ACO.
Nous pouvons succintement commenter l’ouverture dynamique calculée (Fig. 3.20-d) :
A première vue, l’ouverture dynamique semble très grande : extension horizontale jusqu’à
50 mm et verticale au-delà de 50 mm. Cependant, on observe que pour des conditions initiales
verticales ( ) excédant 23 mm (pour x=0 mm), la zone de stabilité résiduelle n’est qu’une
immense île de résonance
) excédant 23 mm (pour x=0 mm), la zone de stabilité résiduelle n’est qu’une
immense île de résonance 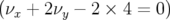 . De plus aux grandes amplitudes, la diffusion est
importante.
. De plus aux grandes amplitudes, la diffusion est
importante.
Une étude plus fine permet d’affirmer que toutes les particules survivantes ayant des conditions initiales dans la sus-dite zone ont leurs nombres d’ondes situés soit sur la résonance principale soit au-delà.
En conclusion, les dimensions de l’ouverture dynamique pour le premier quadrant
(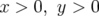 ) doivent être ramenées à des valeurs plus raisonnables :
) doivent être ramenées à des valeurs plus raisonnables : ![[0, 50 ] × [0, 23]](these1195x.png) mm.
mm.
La carte en fréquence associée (Fig. 3.20-c) a également une grande extension dans l’espace des
fréquences. La figure 3.20-c ne la montre pas dans sa totalité : elle est tronquée dans sa partie basse
qui s’étend jusqu’à  . Cependant cette partie n’a pas d’intérêt pour la dynamique, car elle
ne sera jamais atteinte pour la machine réelle (hors de l’ouverture physique, la résonance principale
ne peut être traversée). La description de la carte en fréquence peut être décomposée en deux
parties séparée par la résonance
. Cependant cette partie n’a pas d’intérêt pour la dynamique, car elle
ne sera jamais atteinte pour la machine réelle (hors de l’ouverture physique, la résonance principale
ne peut être traversée). La description de la carte en fréquence peut être décomposée en deux
parties séparée par la résonance 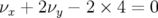 (voir aussi Fig. 3.21 et les cartes en
couleur B.3) :
(voir aussi Fig. 3.21 et les cartes en
couleur B.3) :
(1) une première partie au voisinage du point de fonctionnement 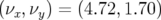 , coin
supérieur droit de la figure. Cette partie est très régulière avec une diffusion faible (équipartition
des points, diffusion faible :
, coin
supérieur droit de la figure. Cette partie est très régulière avec une diffusion faible (équipartition
des points, diffusion faible : 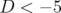 ).
).
(Frontière 1-2) la dynamique est dominée par la résonance systématique d’ordre 3,
 . En pratique, en son voisinage, on observe une grande vitesse d’éjection des
particules. Sur la carte en fréquence soit les particules sont capturées dans l’île de résonance soit il
y a désertion de points : très proche de la résonance, la diffusion est très élevée (
. En pratique, en son voisinage, on observe une grande vitesse d’éjection des
particules. Sur la carte en fréquence soit les particules sont capturées dans l’île de résonance soit il
y a désertion de points : très proche de la résonance, la diffusion est très élevée (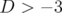 )
correspondant à la proximité des zones hyperboliques associées à la résonance (les particules
vont être perdues si l’intégration est poursuivie). La largeur de la résonance est grande :
)
correspondant à la proximité des zones hyperboliques associées à la résonance (les particules
vont être perdues si l’intégration est poursuivie). La largeur de la résonance est grande :
 .
.
(2) au-delà de la résonance d’ordre 3, la diffusion est importante, la stabilité est faible (les particules ayant des amplitudes initiales horizontales presque nulles sont tout de même stables). Les résonances révélées par la carte en fréquence sont répertoriées dans le tableau 3.6 et localisées sur la figure 3.21.
|
La carte en fréquence est repliée dans la région  (cf. Fig. 3.21). Il semble
qu’au-delà de ce repliement plus aucune trajectoire ne soit stable. Ce repliement correspond dans
l’ouverture dynamique aux amplitudes horizontales supérieures à
(cf. Fig. 3.21). Il semble
qu’au-delà de ce repliement plus aucune trajectoire ne soit stable. Ce repliement correspond dans
l’ouverture dynamique aux amplitudes horizontales supérieures à  (cf. Fig. 3.20-d).
(cf. Fig. 3.20-d).
La figure 3.20-b exhibe le second quadrant (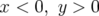 ) de l’ouverture dynamique. La
carte en fréquence (figure 3.20-a) est bien entendu inchangée si ce n’est le caractère
hyperbolique ou elliptique des résonances rencontrées (et l’échantillonnage dans l’espace des
fréquences).
) de l’ouverture dynamique. La
carte en fréquence (figure 3.20-a) est bien entendu inchangée si ce n’est le caractère
hyperbolique ou elliptique des résonances rencontrées (et l’échantillonnage dans l’espace des
fréquences).
L’ouverture dynamique négative a comme extension ![[− 55, 0] × [0, 23] mm](these1217x.png) . Comme
précédemment, toutes les conditions initiales des particules au deçà de la résonance principale
. Comme
précédemment, toutes les conditions initiales des particules au deçà de la résonance principale
 conduisent à des mouvements peu stables (
conduisent à des mouvements peu stables (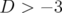 ).
).
La résonance principale,  , est maintenant de nature hyperbolique : c’est
pourquoi on n’observe plus d’île de résonance dans l’ouverture dynamique.
, est maintenant de nature hyperbolique : c’est
pourquoi on n’observe plus d’île de résonance dans l’ouverture dynamique.
La modélisation de Super-ACO peut être améliorée en introduisant les défauts de gradient des quadripôles droits. Les valeurs utilisées sont celles mesurées en 1990 (Barthès et al., 1990) sur l’ensemble des quadripôles de la machine pour un point de fonctionnement équivalent.
|
|
La figure 3.22 indique les valeurs relatives des gradients de chacun des 32 quadripôles de Super-ACO en prenant le troisième quadripôle comme référence. Ces valeurs sont aléatoires et relativement faibles (de l’ordre du pour mille) ; la dynamique globale devrait être peu modifiée bien que la périodicité de l’anneau soit réduite de 4 à 1 : de nouvelles résonances devraient apparaître .
En comparant les cartes en fréquence et ouvertures dynamiques de la machine idéale (Fig. 3.20-a et b) et de la machine avec les défauts de gradients déduits des mesures magnétiques (Fig. 3.23), plusieurs remarques peuvent être faites (voir aussi la carte en couleur B.4).
Le point de fonctionnement est légèrement différent :  , contre
auparavant
, contre
auparavant 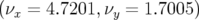 ; toutes les résonances vont être atteintes avec des
amplitudes plus faibles. Cette différence s’explique par la modification des gradients des familles
quadripolaires
; toutes les résonances vont être atteintes avec des
amplitudes plus faibles. Cette différence s’explique par la modification des gradients des familles
quadripolaires 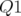 et
et  (le point de fonctionnement n’a pas été réajusté après l’introduction
des défauts).
(le point de fonctionnement n’a pas été réajusté après l’introduction
des défauts).
L’ouverture dynamique est très légèrement réduite. La diffusion est partout plus élevée et en
particulier au voisinage des lignes de résonance (cf. Fig. 3.22-b) et au-delà de la résonance
d’ordre 3 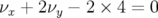 (grandes amplitudes). Le nœud des résonances d’ordre 3,
(grandes amplitudes). Le nœud des résonances d’ordre 3,
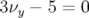 , 9,
, 9,  , 10,
, 10, 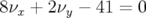 et 7,
et 7,  est
excité.
est
excité.
En conclusion, une détérioration globale de la dynamique est observée mais elle reste faible.