 et des ouvertures dynamiques à
et des ouvertures dynamiques à 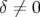 presque nulles
conduisent une durée de vie du faisceau très faible (cf. dynamique longitudinale, limitation par
l’acceptance en énergie).
presque nulles
conduisent une durée de vie du faisceau très faible (cf. dynamique longitudinale, limitation par
l’acceptance en énergie).
Les machines de rayonnement synchrotron de troisième génération sont construites sur des optiques à forte focalisation afin d’atteindre de performances toujours plus extrêmes : les petites émittances créées permettent d’obtenir les hautes brillances recherchées. Cependant, de telles contraintes impliquent l’utilisation de champs magnétiques de forte intensité qui eux-mêmes vont exciter de nombreuses résonances et risquent ainsi de détériorer la dynamique globale du faisceau et de conduire à une faible ouverture dynamique et une faible acceptance en énergie. Il en résulte une injection lente et une faible durée de vie. Ces effets indésirables doivent être minimisés tout en concervant une haute brillance. Une des tâches principales du physicien des accélérateurs se résume d’abord à déterminer la meilleure optique possible de la machine, ensuite à définir une modélisation aussi proche que possible de la réalité et enfin, à développer des méthodes susceptibles d’améliorer la stabilité de la dynamique du faisceau.
L’optique des sources de lumière de troisième génération est construite généralement sur une maille dite Chasman-Green ou double bend achromat1 (Super-ACO, SOLEIL, ESRF) ou une maille triple bend achromat2 (ALS). Les faibles émittances y sont créées en minimisant les fonctions bétatrons dans les dipôles, ce qui se traduit par l’utilisation de forts champs dans les quadripôles adjacents. Nous avons vu (chap. 1, p. § sqq.) que ces derniers créent alors une grande chromaticité naturelle dans les deux plans qui est compensée par l’introduction de lentilles hexapolaires : deux familles, dites chromatiques, suffisent. Cependant très souvent, d’autres familles d’hexapôles sont également introduites dans la maille pour minimiser les largeurs des résonances. La principale difficulté est de déterminer l’emplacement optimum de ces hexapôles autour de l’anneau ainsi que leur force. Seuls des choix judicieux permettent de réduire les nonlinéarités.
La dynamique des particules individuelles est une des causes principales de la limitation des performances des sources de lumière. Si les orbites sont instables aux grandes amplitudes, alors les électrons diffusés à ces grandes amplitudes lors de collisions avec les atomes du gaz résiduel ou avec d’autres électrons (effet Touschek) vont être perdus par le faisceau. Il en sera de même pour les particules injectées à grande amplitude (optimisation de l’injection).
A la connaissance de l’auteur, seule l’ouverture dynamique des particules d’énergie nominale est
optimisée3
pour réduire l’influence des phénomènes nonlinéaires ; ces derniers peuvent conduire à la divergence
rapide des trajectoires des particules et à une chute drastique des performances globales de la
machine. Les ouvertures dynamiques des particules off momentum ne sont que rarement optimisées
pour les sources de lumière. Ce point peut conduire à des situations paradoxales : par exemple, une
très grande ouverture dynamique à  et des ouvertures dynamiques à
et des ouvertures dynamiques à 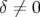 presque nulles
conduisent une durée de vie du faisceau très faible (cf. dynamique longitudinale, limitation par
l’acceptance en énergie).
presque nulles
conduisent une durée de vie du faisceau très faible (cf. dynamique longitudinale, limitation par
l’acceptance en énergie).
Cependant à l’heure actuelle, il n’existe pas de méthode analytique systématique pour arriver à
ces fins (même pour l’optimisation on momentum, i.e. pour  ), la difficulté provenant de la
détermination des amplitudes des résonances. Généralement, le schéma retenu consiste à utiliser
des familles d’hexapôles pour minimiser l’influence des résonances d’ordre trois, considérées comme
les plus néfastes pour la dynamique. Il est souvent admis, mais à tort, que seules les résonances
d’ordre faible sont à corriger (voir le rapport du CERN de Guignard, 1978 où l’auteur reformule
une théorie des perturbations du premier ordre). Pourtant les hexapôles excitent les
résonances de tout ordre (comme nous l’avons observé pour l’application d’Hénon, p. §
sqq.). La méthode utilisée pour Super-ACO ou SOLEIL repose sur le travail réalisé par
Audy (1989) : les coefficients analytiques des amplitudes des résonances d’ordre 3 sont
calculés puis minimisés par ajustement (c’est une méthode de perturbation du premier
ordre).
), la difficulté provenant de la
détermination des amplitudes des résonances. Généralement, le schéma retenu consiste à utiliser
des familles d’hexapôles pour minimiser l’influence des résonances d’ordre trois, considérées comme
les plus néfastes pour la dynamique. Il est souvent admis, mais à tort, que seules les résonances
d’ordre faible sont à corriger (voir le rapport du CERN de Guignard, 1978 où l’auteur reformule
une théorie des perturbations du premier ordre). Pourtant les hexapôles excitent les
résonances de tout ordre (comme nous l’avons observé pour l’application d’Hénon, p. §
sqq.). La méthode utilisée pour Super-ACO ou SOLEIL repose sur le travail réalisé par
Audy (1989) : les coefficients analytiques des amplitudes des résonances d’ordre 3 sont
calculés puis minimisés par ajustement (c’est une méthode de perturbation du premier
ordre).
Deux questions viennent tout de suite à l’esprit : (1) est-il possible de prédire quelles résonances sont susceptibles d’être excitées sur la machine réelle ? (2) est-il possible d’établir une méthode pour identifier facilement les résonances et d’estimer leurs amplitudes ?
Un début de réponse peut être apporté par l’utilisation de la théorie des perturbations en calculant des formes normales. Elles ont été introduites en Physique des Accélérateurs principalement par Dragt et Forest (Université de Maryland) et sont très utilisées au CERN. Bien que donnant de bons résultats (voir par exemple Todesco, Gemmi et Giovannozzi, 1997 et une application au LHC par Papaphilippou et Schmidt, 1998), cette méthode est assez lourde à mettre en œuvre. Des corrections locales sont possibles mais cette méthode dépend fortement de la modélisation et ne permet pas d’effectuer simplement des comparaisons directes entre le modèle et la machine en fonctionnement.
L’Analyse en Fréquence est au contraire une méthode numérique qui permet de manière assez intuitive et pratique d’identifier des résonances et d’estimer leur amplitude. Nous allons l’appliquer à quatre sources de lumière : le Projet SOLEIL, l’ESRF, Super-ACO et l’ALS. Pour chacune de ces machines, nous calculerons des cartes en fréquence ainsi que les ouvertures dynamiques associées. Les résultats seront présentés soit pour une modélisation purement théorique, soit pour une machine en fonctionnement (cf. résultats expérimentaux, chapitres sur l’ALS et Super-ACO). Nous montrerons la grande sensibilité de la dynamique aux réglages magnétiques.
Par soucis de clarification, je tiens à dire que ces deux approches sont complémentaires. La théorie des perturbations a été introduite à une époque où les gros ordinateurs n’existaient pas. Elle a permis et permet encore d’obtenir des formules analytiques relativement simples utilisées pour améliorer le réglage d’un accélérateur et comprendre sa dynamique (e.g. glissement des nombres d’ondes avec l’amplitude, déformation de l’espace des phases, largeur des résonances). Cette méthode ne fonctionne plus si le système est trop perturbé. Elle est moins précise que les intégrateurs numériques pour déterminer les équations du mouvement. La seconde approche repose sur les outils numériques. Elle permet une détermination précise de la trajectoire d’une particule (intégrateurs, codes de tracking) aussi bien pour un régime faiblement que fortement perturbé. Son inconvénient majeur est d’être une « boîte noire » qui fournit peu d’informations pour une compréhension théorique du mouvement nonlinéaire (approche qualitative).
Pour l’ensemble des résultats qui vont être présentés, nous ne prenons en compte que la
dynamique transverse en négligeant le mouvement longitudinal. Ce choix est justifié dans la mesure
où le nombre d’ondes longitudinal 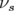 est très faible devant les nombres d’ondes transverses : par
exemple pour SOLEIL, la fréquence longitudinale est
est très faible devant les nombres d’ondes transverses : par
exemple pour SOLEIL, la fréquence longitudinale est  et les nombres d’ondes sont
et les nombres d’ondes sont
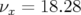 et
et 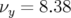 .
.
La majorité des cartes en noir et blanc du corps du mémoire sont reproduites en couleur en annexe B.
SOLEIL [110], acronyme pour Source Optimisée de Lumière d’Energie Intermédiaire de LURE, est une source de rayonnement de hautes performances. Après de nombreux et longs atermoiements, sa construction devrait débuter sur le plateau de Saclay à partir de l’automne 2001 pour des premiers photons fin 2005. La machine vise à remplacer les installations vieillissantes du LURE et à doter la communauté française d’une installation de troisième génération optimisée dans une gamme spectrale complémentaire de l’ESRF, la source européenne de rayonnement synchrotron localisée à Grenoble.
La maille standard de SOLEIL est construite sur une structure dite Chasman-Green modifiée4 (APD SOLEIL, 1999) avec dispersion répartie5. Les principales caractéristiques et les fonctions optiques de la machine sont données par le tableau 3.1 et la figure 3.1. Pour cette étude, la maille de SOLEIL est sans défaut avec sa 4-périodicité. Les chromaticités naturelles sont parfaitement compensées. Les calculs ont été faits pour des particules ayant l’énergie nominale de la machine.
En appliquant le schéma de construction précédemment énoncé (p. §), les cartes en fréquence et les
ouvertures dynamiques ont été calculées pour les deux optiques retenues pour SOLEIL. L’ensemble
des calculs a été réalisé avec le code de tracking DESPOT [42] en intégrant la trajectoire d’une
particule « test » sur  tours. Ce choix est justifié par un temps d’amortissement transverse
de 8.73 ms, i.e. 7 771 tours et un temps d’amortissement longitudinal de 4.35 ms soit 3 872 tours.
Des intégrations à très long terme ont été également entreprises afin de vérifier la validité de
ces hypothèses. Les deux optiques faible émittance retenues et optimisées par l’équipe
faisceau de SOLEIL sont appelées optique faible émittance 1 et 2 (APD SOLEIL, chap. IV
Sources).
tours. Ce choix est justifié par un temps d’amortissement transverse
de 8.73 ms, i.e. 7 771 tours et un temps d’amortissement longitudinal de 4.35 ms soit 3 872 tours.
Des intégrations à très long terme ont été également entreprises afin de vérifier la validité de
ces hypothèses. Les deux optiques faible émittance retenues et optimisées par l’équipe
faisceau de SOLEIL sont appelées optique faible émittance 1 et 2 (APD SOLEIL, chap. IV
Sources).
Pour la première optique, le point de fonctionnement est 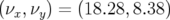 ; Les glissements
des nombres d’ondes avec l’amplitude sont donnés par la figure 3.2-a. Cette optique a été optimisée
pour contraindre la variation du nombre d’ondes horizontal
; Les glissements
des nombres d’ondes avec l’amplitude sont donnés par la figure 3.2-a. Cette optique a été optimisée
pour contraindre la variation du nombre d’ondes horizontal  entre les résonances
entre les résonances
 et
et  .
.
|
A la lecture de la figure 3.3-b, l’ouverture dynamique semble très grande : ![[0, 40] × [0, 24]
y=0 x=0](these1032x.png) mm
cependant ces dimensions doivent être légèrement réduites à
mm
cependant ces dimensions doivent être légèrement réduites à  mm selon
mm selon  (présence d’une île
due à la résonance d’ordre 9) et
(présence d’une île
due à la résonance d’ordre 9) et  mm selon
mm selon  .
.
Le point de fonctionnement est représenté par une croix (en pointillés sur la carte 3.2-b). Il est
presque confondu avec le coin en haut à droite de la carte en fréquence. Le bord supérieur (resp.
inférieur) de la carte correspond au glissement des nombres d’ondes avec l’amplitude horizontale
(resp. verticale) pour la seconde amplitude fixée à  (faible couplage). Pour déchiffrer la
carte 3.3-a (voir aussi la carte en couleur B.1), il est utile de distinguer trois types de
zones :
(faible couplage). Pour déchiffrer la
carte 3.3-a (voir aussi la carte en couleur B.1), il est utile de distinguer trois types de
zones :
 ). Le mouvement est typiquement un mouvement bétatron régulier comme au
voisinage du point de fonctionnement
). Le mouvement est typiquement un mouvement bétatron régulier comme au
voisinage du point de fonctionnement  — aux faibles amplitudes
bétatrons, le mouvement est évidemment linéaire —.
— aux faibles amplitudes
bétatrons, le mouvement est évidemment linéaire —.
 . Selon que la
résonance est traversée au voisinage d’une zone elliptique ou hyperbolique, on observe
soit une accumulation de points soit une désertion (cf. Analyse en Fréquence et pendule
p. §). De manière générale, la diffusion est plus élevée. La particule aura tendance à
osciller transversalement à la résonance. Si la région est bornée de zones régulières, le
mouvement est confiné (cf. discussion sur la diffusion p. §, le schéma 2.11 et infra).
. Selon que la
résonance est traversée au voisinage d’une zone elliptique ou hyperbolique, on observe
soit une accumulation de points soit une désertion (cf. Analyse en Fréquence et pendule
p. §). De manière générale, la diffusion est plus élevée. La particule aura tendance à
osciller transversalement à la résonance. Si la région est bornée de zones régulières, le
mouvement est confiné (cf. discussion sur la diffusion p. §, le schéma 2.11 et infra).
 ) et
qui peut conduire à un comportement fortement nonlinéaire et même chaotique, par
exemple aux grandes amplitudes et sur les bords de l’ouverture dynamique.
) et
qui peut conduire à un comportement fortement nonlinéaire et même chaotique, par
exemple aux grandes amplitudes et sur les bords de l’ouverture dynamique.Pour l’optique ici considérée, la carte en fréquence révèle une dynamique relativement stable, néanmoins plusieurs résonances sont mises en évidence.
La résonance d’ordre 7,  , est atteinte pour
, est atteinte pour  mm (voir la
carte 3.2-b où l’ordre des résonances est le triplet p :q :r défini p. §). On remarquera également un
nœud de résonances juste au-dessus entre cette même résonance et les résonances
mm (voir la
carte 3.2-b où l’ordre des résonances est le triplet p :q :r défini p. §). On remarquera également un
nœud de résonances juste au-dessus entre cette même résonance et les résonances  ,
,
 ,
,  et
et  . Nous pouvons supposer
que si ce nœud de résonances ou la résonance d’ordre 7 sont excités, par exemple par les inévitables
défauts magnétiques, alors la symétrie 4 de l’anneau sera brisée et toutes les orbites
au-delà seront instables. Dans ce cas, l’ouverture dynamique horizontale ne serait plus
que de 24 mm selon
. Nous pouvons supposer
que si ce nœud de résonances ou la résonance d’ordre 7 sont excités, par exemple par les inévitables
défauts magnétiques, alors la symétrie 4 de l’anneau sera brisée et toutes les orbites
au-delà seront instables. Dans ce cas, l’ouverture dynamique horizontale ne serait plus
que de 24 mm selon  . Cet effet est observé lorsque que l’on simule le déplacement
(sciemment exagéré) d’un hexapôle dans l’anneau (cf. carte en fréquence 3.4 à comparer avec
Fig. 3.2-b).
. Cet effet est observé lorsque que l’on simule le déplacement
(sciemment exagéré) d’un hexapôle dans l’anneau (cf. carte en fréquence 3.4 à comparer avec
Fig. 3.2-b).
Plus inquiétant pour la stabilité du faisceau est le nœud entre les résonances d’ordre 7,
 , d’ordre 9,
, d’ordre 9, 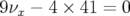 , d’ordre 11,
, d’ordre 11,  et
d’ordre 5,
et
d’ordre 5,  (cf. carte 3.2-b).
(cf. carte 3.2-b).
Il est important de noter que la dynamique est fortement contrainte non seulement par les résonances d’ordre faible, mais aussi par d’ordres plus élevés 9, 11, 13, et ceci, même pour une machine idéale7 . Leur influence est importante à grande amplitude et au voisinage des nœuds de résonances — recouvrement des largeurs de résonances, critère de Chirikov —. Voir pour cela (Laskar, 1993).
Le calcul exhaustif de l’ouverture dynamique ainsi que l’utilisation de la diffusion permet
d’établir une bijection entre l’ouverture dynamique et la carte en fréquence (sauf dans les
régions elliptiques). La localisation des résonances est plus aisée dans les deux espaces, en
particulier celles qui limitent l’ouverture dynamique. Par exemple, la région dans l’ouverture
dynamique vers  mm (protubérance du la figure 3.3-b) correspond aux îles
de la résonance d’ordre 9,
mm (protubérance du la figure 3.3-b) correspond aux îles
de la résonance d’ordre 9,  . Les résonances apparaissent nettement
dans l’ouverture dynamique : ce sont les courbes où la diffusion est plus importante (cf.
Fig. 3.3-b).
. Les résonances apparaissent nettement
dans l’ouverture dynamique : ce sont les courbes où la diffusion est plus importante (cf.
Fig. 3.3-b).
|
|
Enfin, remarquons que la carte en fréquence admet une torsion non définie au voisinage du point de fonctionnement ainsi qu’aux grandes amplitudes. La carte en fréquence 3.2-b se replie sur elle-même (le lecteur peut également s’aider de la figure 3.2-a). Il n’y a alors plus de bijection globale entre la carte en fréquence et l’ouverture dynamique. La torsion non définie a des implications sur la stabilité du faisceau, car elle permet en particulier des directions où la diffusion peut être très rapide (Laskar, 1999).
Pour illustrer différents processus de diffusion, la figure 3.5 (partie inférieure gauche de la carte 3.2-b) représente trois orbites intégrées à long terme, sur 100 000 tours (l’amortissement n’est pas pris en compte, seule la diffusion au voisinage d’une résonance est étudiée).
 mm et de nombres d’ondes
initiaux
mm et de nombres d’ondes
initiaux  . La particule est stable et reste sur la résonance
d’ordre 7,
. La particule est stable et reste sur la résonance
d’ordre 7,  .
.
 mm et de nombres
d’ondes initiaux
mm et de nombres
d’ondes initiaux  , i.e. au voisinage de la résonance
, i.e. au voisinage de la résonance
 . L’orbite diffuse rapidement transversalement à la ligne
de résonance et lentement longitudinalement (diffusion souvent appelée diffusion
d’Arnold). La particule est perdue au bout de 75 000 tours de machine.
. L’orbite diffuse rapidement transversalement à la ligne
de résonance et lentement longitudinalement (diffusion souvent appelée diffusion
d’Arnold). La particule est perdue au bout de 75 000 tours de machine.
 mm et de nombres
d’ondes initiaux
mm et de nombres
d’ondes initiaux  , i.e. au voisinage dans une région de forte
diffusion. La particule diffuse dans l’espace des fréquences rapidement, puis reste
capturée 2 000 tours par la résonance
, i.e. au voisinage dans une région de forte
diffusion. La particule diffuse dans l’espace des fréquences rapidement, puis reste
capturée 2 000 tours par la résonance  et est perdue au bout
de 5 380 tours.
et est perdue au bout
de 5 380 tours.Les résultats précédents m’ont amené à proposer avec P. Nghiem une optique modifiée
(Nadolski, 1998 et chap. IV de l’APD SOLEIL) : comme la résonance d’ordre 9 et le nœud
associé semblent être néfastes pour la dynamique, tout en gardant le même point de
fonctionnement, nous avons contraint la courbe en fréquence de sorte qu’elle n’atteigne
pas cette résonance. Pour cela, nous avons modifié la pente à l’origine de la courbe en
fréquence modifiée de la valeur  à
à  en utilisant les hexapôles (cf.
Fig. 3.7).
en utilisant les hexapôles (cf.
Fig. 3.7).
Comme attendu, le but est atteint tout en conservant pratiquement la même ouverture dynamique (cf. Fig. 3.9 et carte en couleur B.2). Les principales résonances identifiées pour ce réglage sont données par le tableau 3.2 et localisées sur la figure 3.6.
|
|
Dans ce cas, l’extension de la carte en fréquence est réduite, moins de résonances perturbent la dynamique mais en contrepartie, la carte en fréquence est plus repliée sur elle-même (cf. au voisinage du point de fonctionnement et sur la partie gauche de la carte en fréquence 3.6).
Il doit être remarqué que l’allure d’une carte en fréquence est très sensible à une faible modification des forces hexapolaires. La dynamique associée est alors complètement différente alors que les tailles des ouvertures dynamiques ont peu changé (comparer les cartes 3.3-a et 3.9-a).
|
|
Pour l’optique faible émittance numéro 2, le point de fonctionnement est déplacé à
 de manière à ne jamais traverser la résonance d’ordre 7,
de manière à ne jamais traverser la résonance d’ordre 7,  (cf. courbes en fréquence 3.8).
(cf. courbes en fréquence 3.8).
La carte en fréquence et l’ouverture dynamique sont données par la figure 3.10 : bien que l’ouverture dynamique soit légèrement plus petite, elle reste néanmoins plus grande que l’ouverture physique (cf. Tab. 3.2) et surtout la diffusion est bien plus faible que pour la première optique (comparer avec les cartes 3.3 et 3.10).
La carte est deux fois repliée sur elle-même pour cette optique : elle a une faible extension dans l’espace des fréquences et le nombre de résonances rencontrées est bien plus faible. L’influence du repliement de la carte en fréquence sur la dynamique n’a pas fait l’objet d’une étude approfondie pour le présent travail (pour une discussion, voir Laskar, 1999).
|
|
Parmi les deux optiques principales retenues pour SOLEIL, l’optique faible émittance numéro 2 est la plus prometteuse en termes de stabilité du faisceau, taille de l’ouverture dynamique (grande vis-à-vis de l’ouverture physique) avec un très faible nombre de résonances excitées. En particulier, à ouverture dynamique égale, l’optique numéro 2 décrit une dynamique avec une plus faible diffusion que l’optique numéro 1. Nous avons vu néanmoins qu’il est possible d’améliorer l’optique faible émittance 1 sans diminution particulière des autres paramètres caractéristiques (cf. optique 1 modifiée).
En effet le groupe faisceau de SOLEIL a choisi de réaliser une machine relativement souple en termes de réglages et ajustements magnétiques. Six des huit familles d’hexapôles peuvent être utilisées pour modifier l’optimisation sans avoir besoin de déplacer le point de fonctionnement ; des ajustements fins et la réduction de l’influence des résonances peuvent être ainsi facilement envisagés8. Nous devons cependant constater la très grande sensibilité de la dynamique aux forces hexapolaires : l’allure (repliement, extension spatiale) des cartes en fréquence des trois optiques présentées est complètement différente alors que les forces hexapolaires ont été faiblement modifiées.
Ces études devraient être complétées par le calcul de cartes en fréquence et d’ouvertures dynamiques off momentum pour évaluer l’impact des optiques sur l’efficacité d’injection et la durée de vie du faisceau. L’introduction de défauts magnétiques réalistes devrait permettre d’obtenir une estimation raisonnable des performances réelles de la machine en fonctionnement.
Super-ACO [75] est la première machine en France dédiée dès sa construction au rayonnement synchrotron. Mise en fonctionnement en 1987 afin de remplacer l’Anneau de Collision d’Orsay (ACO), Super-ACO est la première source de lumière ayant toutes ses sections droites libres équipées de dispositifs d’insertion9 ; à ce titre, c’est une machine intermédiaire entre la deuxième et la troisième génération (son émittance verticale est trop grande pour être classée dans la dernière catégorie). Les particules stockées sont des positrons.
Super-ACO est une machine d’énergie intermédiaire,  , constituée de quatre
super-périodes (cf. synoptique de la machine 3.11). La maille standard, i.e. une super-période, suit
une structure Chasman-Green avec un plan de symétrie (cf. schéma 3.12). Les principales
caractéristiques de l’anneau de stockage sont rassemblées dans le tableau 3.3.
, constituée de quatre
super-périodes (cf. synoptique de la machine 3.11). La maille standard, i.e. une super-période, suit
une structure Chasman-Green avec un plan de symétrie (cf. schéma 3.12). Les principales
caractéristiques de l’anneau de stockage sont rassemblées dans le tableau 3.3.
|
|
De par leurs particularités, il est intéressant de donner une brève description des différents éléments magnétiques de Super-ACO :
 .
La valeur de l’angle des coins des dipôles est ajustée sur les mesures expérimentales
(Level et Nghiem, 1986). Pour obtenir la même avance de phase, l’angle n’est pas
.
La valeur de l’angle des coins des dipôles est ajustée sur les mesures expérimentales
(Level et Nghiem, 1986). Pour obtenir la même avance de phase, l’angle n’est pas
 ˚mais
˚mais  ˚(cf. le schéma d’un aimant à faces parallèles 2.2 p. §).
˚(cf. le schéma d’un aimant à faces parallèles 2.2 p. §).
 , une bobine hexapolaire de champ maximum
, une bobine hexapolaire de champ maximum  , une
bobine dipolaire, pour compenser la composante dipolaire créée par la bobine hexapolaire et
deux bobines de correction (pour correction dipolaire horizontale, dipolaire verticale ou
quadripolaire). L’hexapôle (
, une
bobine dipolaire, pour compenser la composante dipolaire créée par la bobine hexapolaire et
deux bobines de correction (pour correction dipolaire horizontale, dipolaire verticale ou
quadripolaire). L’hexapôle ( ) possède un terme décapolaire important simulé par
une lentille décapolaire (
) possède un terme décapolaire important simulé par
une lentille décapolaire ( ). Le quadripôle est ainsi modélisé par un champ
quadripolaire, une composante hexapolaire et une lentille décapolaire (cf. schéma
équivalent 3.14).
). Le quadripôle est ainsi modélisé par un champ
quadripolaire, une composante hexapolaire et une lentille décapolaire (cf. schéma
équivalent 3.14).
Le point de fonctionnement est ajusté à l’aide des familles quadripolaires  et
et  , la
fonction dispersion à l’aide des familles
, la
fonction dispersion à l’aide des familles  et
et  .
.
|
|
 et
et  situées dans
l’achromat11
sont utilisées pour ajuster les chromaticités ; les familles
situées dans
l’achromat11
sont utilisées pour ajuster les chromaticités ; les familles  et
et  sont réglées pour
minimiser l’amplitude des résonances d’ordre trois induites par les hexapôles (Audy,
1989).
sont réglées pour
minimiser l’amplitude des résonances d’ordre trois induites par les hexapôles (Audy,
1989).
 ) et hexapolaires (
) et hexapolaires ( ) sont reliées par la
relation
) sont reliées par la
relation  (Brunelle et al., 1999 et communication personnelle de Pascale
Brunelle).
(Brunelle et al., 1999 et communication personnelle de Pascale
Brunelle).L’ouverture physique horizontale est limitée par le
septum12
situé à  mm vers l’intérieur de l’anneau et vers l’extérieur par la chambre à vide à
mm vers l’intérieur de l’anneau et vers l’extérieur par la chambre à vide à
 mm. Verticalement, la limite est donnée par les dimensions de la chambre à vide dans les
onduleurs, soit
mm. Verticalement, la limite est donnée par les dimensions de la chambre à vide dans les
onduleurs, soit  mm.
mm.
Pour effectuer cette étude, plusieurs logiciels pouvaient être utilisés13 :
Le programme DESPOT a dû être abandonné dès le début pour cette étude, car il ne modélise pas les champs de fuite d’un dipôle : tout le code est écrit dans l’approximation des grandes machines.
Le programme BETA a l’inconvénient d’être lourdement interfacé et interactif, rendant son utilisation difficile pour des calculs longs tels ceux d’une carte en fréquence. Cependant étant utilisé au LURE, dans un premier temps, il n’a pas été écarté.
L’ensemble de la discussion va porter sur une description de Super-ACO sans défaut, i.e. pour une machine idéale.
Lorsque les champs de fuite sont inclus dans le modèle de la dynamique, les calculs
effectués avec le code BETA à l’ordre 2 ne sont plus symplectiques. En fait, leur inclusion
dans le développement de Taylor d’ordre 2 « tue » la symplecticité de l’intégrateur (cf.
Fig. 3.15). Si l’on appelle 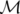 l’application de transfert et
l’application de transfert et  sa matrice jacobienne,
alors par définition la transformation est symplectique si et seulement si (Goldstein,
1980) :
sa matrice jacobienne,
alors par définition la transformation est symplectique si et seulement si (Goldstein,
1980) :
 |
avec 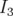 et
et 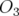 respectivement les matrices identité et nulle de rang 3. Ces conditions de
symplecticité se traduisent par 15 relations pour un système à 3 degrés de liberté. Dans le logiciel
BETA, la matrice de transfert prend en compte les termes du second ordre. Ainsi programmé, le
nombre de relations de symplecticité est plus élevé (quelques conditions devant être théoriquement
nulles, si le schéma d’intégration est symplectique, sont données par le tableau 3.4). Il ne
faut donc pas utiliser BETA au second ordre pour Super-ACO mais utiliser l’ordre dit
scaling14
qui prend correctement en compte les champs de fuite.
respectivement les matrices identité et nulle de rang 3. Ces conditions de
symplecticité se traduisent par 15 relations pour un système à 3 degrés de liberté. Dans le logiciel
BETA, la matrice de transfert prend en compte les termes du second ordre. Ainsi programmé, le
nombre de relations de symplecticité est plus élevé (quelques conditions devant être théoriquement
nulles, si le schéma d’intégration est symplectique, sont données par le tableau 3.4). Il ne
faut donc pas utiliser BETA au second ordre pour Super-ACO mais utiliser l’ordre dit
scaling14
qui prend correctement en compte les champs de fuite.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Si les champs de fuite des dipôles sont négligés, au second ordre, le système intégré reste
symplectique (comme on l’attend), mais uniquement à très faible amplitude (e.g.  mm).
Par contre dès
mm).
Par contre dès 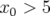 mm, l’espace des phases se peuple de trajectoires spirales caractéristiques
ici encore de la non-symplecticité. Après quelques discussions fructueuses avec J. Payet, il s’avère
que la seconde raison de non-symplecticité est le faible rayon de courbure de Super-ACO,
mm, l’espace des phases se peuple de trajectoires spirales caractéristiques
ici encore de la non-symplecticité. Après quelques discussions fructueuses avec J. Payet, il s’avère
que la seconde raison de non-symplecticité est le faible rayon de courbure de Super-ACO,
 m. Notons cependant que ce problème est général pour pratiquement tous les logiciels de
tracking — second ordre de MAD compris — car l’approximation des grands rayons de courbure,
abusivement utilisée, est souvent oubliée.
m. Notons cependant que ce problème est général pour pratiquement tous les logiciels de
tracking — second ordre de MAD compris — car l’approximation des grands rayons de courbure,
abusivement utilisée, est souvent oubliée.
La conclusion est l’obligation d’utiliser le code BETA à l’ordre scaling pour tous les calculs de Super-ACO.
Une fois ces premiers problèmes cernés, une comparaison des résultats obtenus avec les logiciels BETA et MAD a été réalisée. Rappelons que parmi les critères recherchés, la rapidité de calcul et la validité du code à grandes amplitudes sur un grand nombre de tours sont primordiales pour utiliser l’Analyse en Fréquence.
La figure 3.16 illustre un bogue lors du calcul de la contribution des multipôles dans BETA. Alors qu’à l’ordre scaling, les résultats devraient être strictement identiques en mode15 XZ ou QXZ, ils sont totalement dissemblables, en particulier pour la variation du nombre d’ondes horizontal avec l’amplitude. Après discussion avec J. Payet, il s’avère que les calculs doivent être réalisés en mode XZ (plus lent que le mode QXZ mais « moins imprécis » !).
|
|
Ajoutons enfin, que l’ordre scaling est une approximation qui est valide seulement à faible
amplitude. En comparant les résultats entre BETA et MAD, il s’avère que les résultats diffèrent dès
 mm16,
amplitude relativement faible puisque l’acceptance physique de la machine est
mm16,
amplitude relativement faible puisque l’acceptance physique de la machine est  mm !
Au-delà, les résultats de BETA sont complètement faux, car les approximations de calcul ne sont
plus vérifiées.
mm !
Au-delà, les résultats de BETA sont complètement faux, car les approximations de calcul ne sont
plus vérifiées.
Dans la suite, sauf cas explicitement dit, je n’utilise plus que l’intégrateur LIE4 de MAD qui est assez lent mais « exact » à grande amplitude car symplectique d’ordre quatre.
Pour finir, remarquons qu’on n’observe pas de différence notable pour le calcul de  avec BETA mode QXZ, XZ ou LIE4 de MAD. Ce résultat se comprend immédiatement, car les
lentilles décapolaires induisent le champ magnétique suivant :
avec BETA mode QXZ, XZ ou LIE4 de MAD. Ce résultat se comprend immédiatement, car les
lentilles décapolaires induisent le champ magnétique suivant :
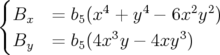 | (3.1) |
où 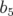 est la force octupolaire (cf. l’expression générale 1.46 du champ magnétique, p. §). Or les
calculs précédents ont été réalisés pour
est la force octupolaire (cf. l’expression générale 1.46 du champ magnétique, p. §). Or les
calculs précédents ont été réalisés pour  ou
ou  (couplage non pris en compte dans ce
type de calcul par le code BETA) ; les champs magnétiques se simplifient dans le premier cas à
(couplage non pris en compte dans ce
type de calcul par le code BETA) ; les champs magnétiques se simplifient dans le premier cas à
 et dans le second cas à
et dans le second cas à  . Donc, il n’y a pas d’influence
notable dans le plan vertical.
. Donc, il n’y a pas d’influence
notable dans le plan vertical.
Malgré ses qualités, le code BETA n’est pas adapté pour effectuer de longues intégrations numériques et des optimisations à grandes amplitudes (pour une machine à faible rayon de courbure). D’ailleurs, il n’a pas été écrit dans cette optique (cf. les approximations réalisées).
Super-ACO est considéré comme machine parfaite, i.e. sans défauts avec sa 4-périodicité. Les
onduleurs ou wigglers ne sont pas modélisés et de plus les forces des lentilles décapolaires sont
surestimées17
d’un facteur  :
:  .
.
Le point de fonctionnement a pour nombres d’ondes  et
et 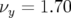 et les hexapôles
chromatiques sont ajustés pour une chromaticité nulle dans les deux plans (tableau 3.5). L’ensemble
des calculs est réalisé pour des particules d’énergie nominale (
et les hexapôles
chromatiques sont ajustés pour une chromaticité nulle dans les deux plans (tableau 3.5). L’ensemble
des calculs est réalisé pour des particules d’énergie nominale ( ). Les fonctions optiques pour
une super-période sont données par la figure 3.17.
). Les fonctions optiques pour
une super-période sont données par la figure 3.17.
|
Les calculs effectués avec le logiciel BETA diffèrent de ceux du logiciel MAD tout particulièrement pour des intégrations à grandes amplitudes. Nous l’avons déjà vérifié dans la section précédente. Les courbes de glissement des nombres d’ondes (Fig. 3.18) sont obtenues en utilisant l’intégrateur LIE4 de MAD.
Il est intéressant de comparer les ouvertures dynamiques calculées avec le logiciel BETA et avec
le code MAD (Fig. 3.19). La méthode de calcul de l’ouverture dynamique de BETA et celle
présentée avec MAD sont radicalement différentes. La philosophie de BETA est de ne tracer que le
bord de l’ouverture dynamique selon le schéma suivant. On se donne une amplitude  à
à
 fixé, on commence l’intégration, si l’on est stable (resp. instable), on incrémente
(resp. décrémente)
fixé, on commence l’intégration, si l’on est stable (resp. instable), on incrémente
(resp. décrémente) 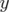 jusqu’à être instable (resp. stable). Ensuite,
jusqu’à être instable (resp. stable). Ensuite,  est incrémenté et
l’on réitère le processus précédent. Notons que par cette méthode, on n’explore pas
l’intérieur de l’ouverture dynamique qui peut alors contenir des régions conduisant à des
mouvements instables. Un des points forts de cette méthode est la rapidité du temps de calcul
qui permet de l’utiliser pour l’optimisation d’une machine pour un faible nombre de
tours.
est incrémenté et
l’on réitère le processus précédent. Notons que par cette méthode, on n’explore pas
l’intérieur de l’ouverture dynamique qui peut alors contenir des régions conduisant à des
mouvements instables. Un des points forts de cette méthode est la rapidité du temps de calcul
qui permet de l’utiliser pour l’optimisation d’une machine pour un faible nombre de
tours.
|
|
Dans le second cas, on n’utilise MAD que pour réaliser l’intégration numérique de la trajectoire.
On se donne une grille de conditions initiales 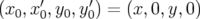 et pour chaque nœud du
maillage, on effectue l’intégration et l’on ne garde que les conditions initiales qui ont conduit à un
mouvement stable. Ce type de calcul est beaucoup plus long, mais il est exhaustif au sens où l’on est
assuré de ne pas avoir de région instable contenue dans l’ouverture dynamique, pourvu que le
maillage soit assez fin (typiquement 150
et pour chaque nœud du
maillage, on effectue l’intégration et l’on ne garde que les conditions initiales qui ont conduit à un
mouvement stable. Ce type de calcul est beaucoup plus long, mais il est exhaustif au sens où l’on est
assuré de ne pas avoir de région instable contenue dans l’ouverture dynamique, pourvu que le
maillage soit assez fin (typiquement 150 150 conditions initiales avec un pas suivant une loi en
racine carrée).
150 conditions initiales avec un pas suivant une loi en
racine carrée).
Dans la présente étude, cette méthode donne des résultats peu différents qualitativement mais complètement différents quantitativement (bijection entre ouverture dynamique et carte en fréquence, localisation des résonances, stabilité).
L’ouverture dynamique (figure 3.20-d) et la carte en fréquence (figure 3.20-c) ont été calculées en
intégrant la trajectoire de 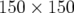 conditions initiales réparties dans le premier quadrant
(
conditions initiales réparties dans le premier quadrant
( ) de l’espace des configurations
) de l’espace des configurations ![(x,y) ∈ [0,50] × [0,60] mm](these1183x.png) . L’intégration est
effectuée sur deux fois 1 000 tours. Les 1 000 premiers tours sont utilisés pour calculer
les fréquences associées au mouvement d’une particule survivante et les 1 000 suivants
pour calculer la diffusion de l’orbite. Ce choix n’est pas arbitraire mais est justifié par
une rapide convergence de l’application fréquence. Rappelons que, grâce aux propriétés
de l’Analyse en Fréquence, l’on est dispensé de réaliser une intégration numérique des
trajectoires pour un nombre de tours de 75 000 correspondant au temps d’amortissement de
Super-ACO.
. L’intégration est
effectuée sur deux fois 1 000 tours. Les 1 000 premiers tours sont utilisés pour calculer
les fréquences associées au mouvement d’une particule survivante et les 1 000 suivants
pour calculer la diffusion de l’orbite. Ce choix n’est pas arbitraire mais est justifié par
une rapide convergence de l’application fréquence. Rappelons que, grâce aux propriétés
de l’Analyse en Fréquence, l’on est dispensé de réaliser une intégration numérique des
trajectoires pour un nombre de tours de 75 000 correspondant au temps d’amortissement de
Super-ACO.
|
|
Nous pouvons succintement commenter l’ouverture dynamique calculée (Fig. 3.20-d) :
A première vue, l’ouverture dynamique semble très grande : extension horizontale jusqu’à
50 mm et verticale au-delà de 50 mm. Cependant, on observe que pour des conditions initiales
verticales ( ) excédant 23 mm (pour x=0 mm), la zone de stabilité résiduelle n’est qu’une
immense île de résonance
) excédant 23 mm (pour x=0 mm), la zone de stabilité résiduelle n’est qu’une
immense île de résonance 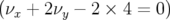 . De plus aux grandes amplitudes, la diffusion est
importante.
. De plus aux grandes amplitudes, la diffusion est
importante.
Une étude plus fine permet d’affirmer que toutes les particules survivantes ayant des conditions initiales dans la sus-dite zone ont leurs nombres d’ondes situés soit sur la résonance principale soit au-delà.
En conclusion, les dimensions de l’ouverture dynamique pour le premier quadrant
(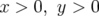 ) doivent être ramenées à des valeurs plus raisonnables :
) doivent être ramenées à des valeurs plus raisonnables : ![[0, 50 ] × [0, 23]](these1195x.png) mm.
mm.
La carte en fréquence associée (Fig. 3.20-c) a également une grande extension dans l’espace des
fréquences. La figure 3.20-c ne la montre pas dans sa totalité : elle est tronquée dans sa partie basse
qui s’étend jusqu’à  . Cependant cette partie n’a pas d’intérêt pour la dynamique, car elle
ne sera jamais atteinte pour la machine réelle (hors de l’ouverture physique, la résonance principale
ne peut être traversée). La description de la carte en fréquence peut être décomposée en deux
parties séparée par la résonance
. Cependant cette partie n’a pas d’intérêt pour la dynamique, car elle
ne sera jamais atteinte pour la machine réelle (hors de l’ouverture physique, la résonance principale
ne peut être traversée). La description de la carte en fréquence peut être décomposée en deux
parties séparée par la résonance 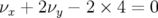 (voir aussi Fig. 3.21 et les cartes en
couleur B.3) :
(voir aussi Fig. 3.21 et les cartes en
couleur B.3) :
(1) une première partie au voisinage du point de fonctionnement 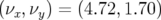 , coin
supérieur droit de la figure. Cette partie est très régulière avec une diffusion faible (équipartition
des points, diffusion faible :
, coin
supérieur droit de la figure. Cette partie est très régulière avec une diffusion faible (équipartition
des points, diffusion faible : 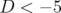 ).
).
(Frontière 1-2) la dynamique est dominée par la résonance systématique d’ordre 3,
 . En pratique, en son voisinage, on observe une grande vitesse d’éjection des
particules. Sur la carte en fréquence soit les particules sont capturées dans l’île de résonance soit il
y a désertion de points : très proche de la résonance, la diffusion est très élevée (
. En pratique, en son voisinage, on observe une grande vitesse d’éjection des
particules. Sur la carte en fréquence soit les particules sont capturées dans l’île de résonance soit il
y a désertion de points : très proche de la résonance, la diffusion est très élevée (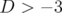 )
correspondant à la proximité des zones hyperboliques associées à la résonance (les particules
vont être perdues si l’intégration est poursuivie). La largeur de la résonance est grande :
)
correspondant à la proximité des zones hyperboliques associées à la résonance (les particules
vont être perdues si l’intégration est poursuivie). La largeur de la résonance est grande :
 .
.
(2) au-delà de la résonance d’ordre 3, la diffusion est importante, la stabilité est faible (les particules ayant des amplitudes initiales horizontales presque nulles sont tout de même stables). Les résonances révélées par la carte en fréquence sont répertoriées dans le tableau 3.6 et localisées sur la figure 3.21.
|
La carte en fréquence est repliée dans la région  (cf. Fig. 3.21). Il semble
qu’au-delà de ce repliement plus aucune trajectoire ne soit stable. Ce repliement correspond dans
l’ouverture dynamique aux amplitudes horizontales supérieures à
(cf. Fig. 3.21). Il semble
qu’au-delà de ce repliement plus aucune trajectoire ne soit stable. Ce repliement correspond dans
l’ouverture dynamique aux amplitudes horizontales supérieures à  (cf. Fig. 3.20-d).
(cf. Fig. 3.20-d).
La figure 3.20-b exhibe le second quadrant (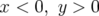 ) de l’ouverture dynamique. La
carte en fréquence (figure 3.20-a) est bien entendu inchangée si ce n’est le caractère
hyperbolique ou elliptique des résonances rencontrées (et l’échantillonnage dans l’espace des
fréquences).
) de l’ouverture dynamique. La
carte en fréquence (figure 3.20-a) est bien entendu inchangée si ce n’est le caractère
hyperbolique ou elliptique des résonances rencontrées (et l’échantillonnage dans l’espace des
fréquences).
L’ouverture dynamique négative a comme extension ![[− 55, 0] × [0, 23] mm](these1217x.png) . Comme
précédemment, toutes les conditions initiales des particules au deçà de la résonance principale
. Comme
précédemment, toutes les conditions initiales des particules au deçà de la résonance principale
 conduisent à des mouvements peu stables (
conduisent à des mouvements peu stables (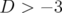 ).
).
La résonance principale,  , est maintenant de nature hyperbolique : c’est
pourquoi on n’observe plus d’île de résonance dans l’ouverture dynamique.
, est maintenant de nature hyperbolique : c’est
pourquoi on n’observe plus d’île de résonance dans l’ouverture dynamique.
La modélisation de Super-ACO peut être améliorée en introduisant les défauts de gradient des quadripôles droits. Les valeurs utilisées sont celles mesurées en 1990 (Barthès et al., 1990) sur l’ensemble des quadripôles de la machine pour un point de fonctionnement équivalent.
|
|
La figure 3.22 indique les valeurs relatives des gradients de chacun des 32 quadripôles de Super-ACO en prenant le troisième quadripôle comme référence. Ces valeurs sont aléatoires et relativement faibles (de l’ordre du pour mille) ; la dynamique globale devrait être peu modifiée bien que la périodicité de l’anneau soit réduite de 4 à 1 : de nouvelles résonances devraient apparaître .
En comparant les cartes en fréquence et ouvertures dynamiques de la machine idéale (Fig. 3.20-a et b) et de la machine avec les défauts de gradients déduits des mesures magnétiques (Fig. 3.23), plusieurs remarques peuvent être faites (voir aussi la carte en couleur B.4).
Le point de fonctionnement est légèrement différent :  , contre
auparavant
, contre
auparavant 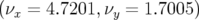 ; toutes les résonances vont être atteintes avec des
amplitudes plus faibles. Cette différence s’explique par la modification des gradients des familles
quadripolaires
; toutes les résonances vont être atteintes avec des
amplitudes plus faibles. Cette différence s’explique par la modification des gradients des familles
quadripolaires 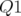 et
et  (le point de fonctionnement n’a pas été réajusté après l’introduction
des défauts).
(le point de fonctionnement n’a pas été réajusté après l’introduction
des défauts).
L’ouverture dynamique est très légèrement réduite. La diffusion est partout plus élevée et en
particulier au voisinage des lignes de résonance (cf. Fig. 3.22-b) et au-delà de la résonance
d’ordre 3 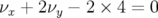 (grandes amplitudes). Le nœud des résonances d’ordre 3,
(grandes amplitudes). Le nœud des résonances d’ordre 3,
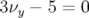 , 9,
, 9,  , 10,
, 10, 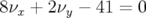 et 7,
et 7,  est
excité.
est
excité.
En conclusion, une détérioration globale de la dynamique est observée mais elle reste faible.
Suite aux études précédentes, nous souhaitions calculer une carte en fréquence correspondant aux conditions expérimentales nominales en termes de chromaticités, valeurs de courants quadripolaires et hexapolaires. Peut-être comprendrions-nous alors mieux les performances actuelles de Super-ACO. Seuls les dispositifs d’insertions n’ont pas été modélisés.
Le point de fonctionnement a pour nombres d’ondes : 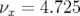 et
et  (cf. tableau
3.7). Les valeurs des chromaticités réduites désormais non nulles,
(cf. tableau
3.7). Les valeurs des chromaticités réduites désormais non nulles, 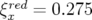 et
et 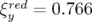 ,
sont réglées par ajustement des forces de deux familles hexapolaires
,
sont réglées par ajustement des forces de deux familles hexapolaires  et
et  . Les
valeurs des courants des quadripôles et hexapôles sont données dans le tableau 3.8 et les
fonctions optiques par la figure 3.24. La fonction dispersion est toujours nulle en dehors des
achromats.
. Les
valeurs des courants des quadripôles et hexapôles sont données dans le tableau 3.8 et les
fonctions optiques par la figure 3.24. La fonction dispersion est toujours nulle en dehors des
achromats.
|
|
Les glissements de nombres d’ondes avec l’amplitude sont donnés en comparaison avec ceux calculés par le code BETA (Fig. 3.25).
L’ouverture dynamique est réduite dans le plan horizontal à -30 mm (cf. Fig. 3.26-b). La carte
en fréquence (cf. Fig. 3.26-a, voir aussi la carte en couleur B.5) présente un repliement important,
sa lecture est alors difficile. La dynamique est fortement marquée par la résonance d’ordre 3,
 qui limite l’ouverture dynamique verticale à 20 mm. Il faut cependant noter qu’en
expérience, l’ouverture dynamique verticale mesurée est bien plus petite, de l’ordre de 12 mm
(l’ouverture physique est à 15 mm).
qui limite l’ouverture dynamique verticale à 20 mm. Il faut cependant noter qu’en
expérience, l’ouverture dynamique verticale mesurée est bien plus petite, de l’ordre de 12 mm
(l’ouverture physique est à 15 mm).
Nous avons vu que Super-ACO est une machine singulière de par son faible rayon de courbure, ses champs de fuite et coins dipolaires non négligeables. L’approximation traditionnelle des grandes machines n’est plus valable et l’approximation hard edge n’est plus suffisante. Nous avons insisté également à plusieurs reprises sur le fait que le code BETA n’est pas adapté pour réaliser des études d’optimisation de la dynamique à long terme et pour des amplitudes supérieures à environ 20 mm pour une machine telle que Super-ACO, même si l’optique linéaire est toujours bien traitée.
Des cartes en fréquence et ouvertures dynamiques ont été calculées pour différentes
configurations machines qui juste qu’en l’an 2000 étaient considérées comme reflétant la machine en
fonctionnement. Cependant, cette étude n’a pas permis d’expliquer correctement certaines
observations expérimentales. En effet, l’ouverture dynamique est limitée dans le plan vertical en
expérience, la dynamique du faisceau est sensible à une résonance d’ordre 3 (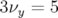 ). Or nous
n’avons pas réussi à confirmer ses observations (à faibles amplitudes) à partir du modèle de
l’anneau.
). Or nous
n’avons pas réussi à confirmer ses observations (à faibles amplitudes) à partir du modèle de
l’anneau.
Un problème crucial est de pouvoir arriver à définir un modèle aussi réaliste que possible de l’anneau de stockage. Ce besoin se justifie, car d’une part, il permettrait de mieux prédire le comportement de la machine réelle et d’autre part de pouvoir rapidement identifier les causes d’une modification des performances de l’accélérateur.
Il est utile de dresser un bref tableau des principaux accords et désaccords entre le modèle actuel et l’expérience — en nous restreignant à la seule dynamique transverse —.
|
|
Nous disposons d’un excellent modèle de l’optique linéaire : point de fonctionnement, faible battement des fonctions bétatrons, bonne efficacité des correcteurs dipolaires utilisés pour corriger l’orbite fermée.
Les valeurs des coins et champs de fuite des dipôles ont été ajustées sur l’expérience (Level et Nghiem, 1986). La caractérisation nonlinéaire des forces des quadripôles et hexapôles a été faite en 1989 par P. Nghiem, des mesures magnétiques sur banc d’essai à la fin des années 1990 (Barthès et al., 1990). Le glissement des nombres d’ondes avec l’énergie est également en accord avec les mesures expérimentales suite à l’introduction d’une composante décapolaires induites par les hexapôles qui sont créés par un « mauvais dipôle » (Brunelle et al., 1999). Un important travail de caractérisation de l’impact des éléments d’insertion sur la dynamique transverse a été réalisé à Super-ACO (Brunelle, 1992, Sommer et al., 1992)
Par contre, les mesures de durée de vie Touschek, de valeurs de chromaticités, de taille de l’ouverture dynamique et d’acceptance en énergie ne sont pas encore bien comprises.
Nous devons également rappeler que Super-ACO n’est pas équipé de moniteur de position tour par tour ni de perturbateur vertical. Si bien qu’aucune caractérisation de la variation des nombres d’ondes avec l’amplitude n’a été réalisée (nous verrons qu’une des caractéristiques de l’ALS est de disposer d’un grand nombre d’outils de diagnostic et d’exploration de la dynamique de l’anneau).
Dans la seconde partie dédiée aux résultats expérimentaux, nous verrons comment nous pouvons améliorer le modèle de Super-ACO. La première idée sera d’obtenir une estimation réaliste des défauts magnétiques de la machine. Peut-être, qu’à l’image de l’ALS (voir page § sqq.), la dynamique se trouverait fortement modifiée. Puis, nous explorerons la dynamique de l’anneau à travers les glissements des nombres d’ondes avec l’amplitude horizontale en utilisant une électrode tour par tour, le perturbateur horizontal et l’Analyse en Fréquence.
L’installation européenne de radiation synchrotron (European Synchrotron Radiation Facility,
ESRF [38] et [37]) est actuellement la meilleure source de lumière de troisième génération en termes
de performances. Mise en service en 1992 (premiers photons), l’optique possède une périodicité 16,
ce qui permet de réduire drastiquement le nombre de résonances permises. La maille suit un schéma
Chasman-Green avec dispersion distribuée et des sections droites alternant faibles et grandes
fonctions bétatrons (cf. Fig. 3.27). En opération, il est nécessaire de surcompenser les chromaticités
à des valeurs légèrement positives. Les principaux paramètres de l’ESRF sont donnés par le
tableau 3.9. L’acceptance en énergie mesurée est de 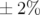 , l’injection est réalisée au voisinage du
point
, l’injection est réalisée au voisinage du
point  mm.
mm.
La présente étude est restreinte aux deux jeux hexapolaires nominaux. Expérimentalement, le second semble meilleur pour un fort courant par paquet où la durée de vie est plus courte (communication personnelle de A. Ropert, 1999). Nous allons essayer de le comprendre à travers l’Analyse en Fréquence. L’intégration numérique a été effectuée avec le programme MAD version 8 [50] pour des particules on et off momemtum, sur deux fois 1 000 tours d’une machine constituée d’une seule super-période, soit 125 tours de machine réelle. Le temps d’amortissement de l’ESRF est d’environ 2 000 tours.
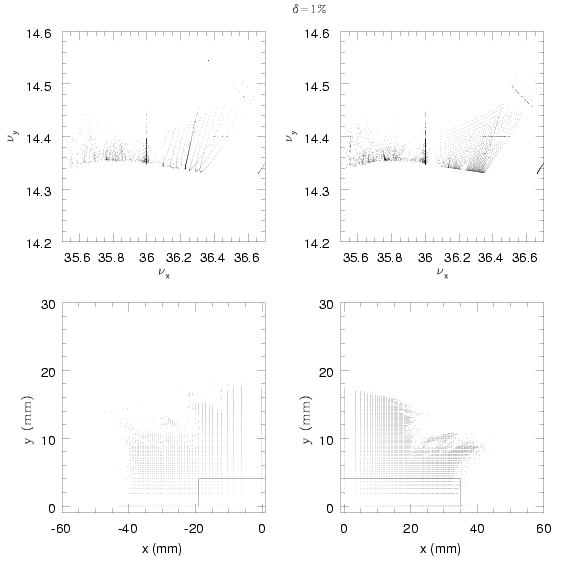
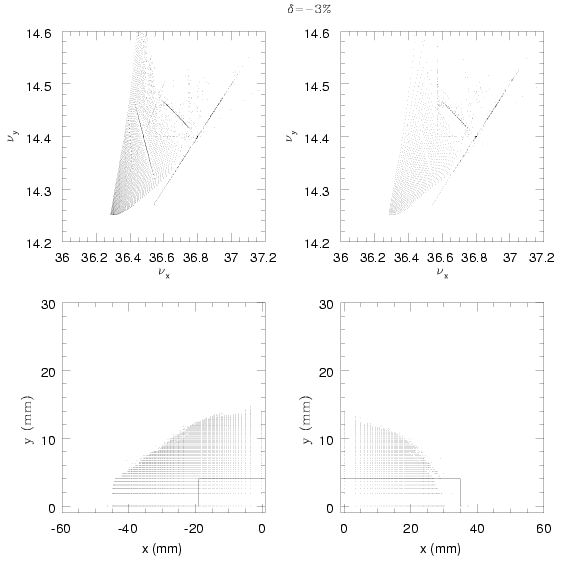
La figure 3.28 exhibe l’ouverture dynamique on momentum de l’ESRF ; à première vue, elle
semble très grande, irrégulière, fortement marquée par les résonances et dissymétrique :
![[−56,42]y=0 × [− 16,16]x=0](these1303x.png) mm (
mm ( et
et  ). Néanmoins, ces dimensions sont
beaucoup trop optimistes et doivent être réduites. En effet, une analyse plus détaillée de l’intérieur
de l’ouverture dynamique révèle de nombreux îlots de résonance.
). Néanmoins, ces dimensions sont
beaucoup trop optimistes et doivent être réduites. En effet, une analyse plus détaillée de l’intérieur
de l’ouverture dynamique révèle de nombreux îlots de résonance.
|
|
Pour lever tout hypothétique interrogation au sujet des calculs des cartes en fréquence, je
rappelle au lecteur que la dynamique de la particule ne change pas si les conditions initiales des
particules sont choisies dans le quart de l’espace des configurations ( ) ou
(
) ou
( ).
).
La lecture d’une carte en fréquence de l’ESRF (Fig. 3.29-a, voir aussi les cartes B.10) est plus délicate que celle de SOLEIL, puisque la carte présente un repliement important. Afin de faciliter la lecture, la carte peut être divisée en deux parties (voir Fig. 3.30) :
 mm selon
mm selon  ; les limites sont
données par la résonance entière
; les limites sont
données par la résonance entière  et l’amplitude verticale
et l’amplitude verticale  mm ;
la diffusion y est faible. Notons cependant la présence de la résonance d’ordre 5,
mm ;
la diffusion y est faible. Notons cependant la présence de la résonance d’ordre 5,
 atteinte pour
atteinte pour  mm dans l’espace des configurations
(
mm dans l’espace des configurations
( mm si l’on considère l’ouverture dynamique négative).
mm si l’on considère l’ouverture dynamique négative).
![x ∈ [− 41, − 28] ∪ [20, 30]](these1318x.png) mm sont capturées dans l’île de la résonance
entière
mm sont capturées dans l’île de la résonance
entière  .
.Le codage de la diffusion sur l’ouverture dynamique met bien en exergue les régions
hyperboliques, les régions elliptiques et les résonances. L’injection est réalisée au voisinage de la
résonance d’ordre 5,  .
.
Forts de ces résultats, nous pouvons donner des dimensions de l’ouverture dynamique plus
réalistes, sachant qu’en pratique une résonance entière ne peut être traversée sans perte
significative des performances du faisceau : ![[− 27, 21]y=0 × [− 7, 7]x=0](these1321x.png) mm, soit une réduction d’un
facteur deux dans les deux directions transverses.
mm, soit une réduction d’un
facteur deux dans les deux directions transverses.
Bien évidemment, si l’on prend en compte les défauts multipolaires, la symétrie 16 est brisée, les largeurs de résonance sont plus importantes et risquent de se recouvrir ; la zone de stabilité dans l’espace des fréquences sera encore plus petite.
|
|
|
|
Enfin lorsque l’on calcule le glissement des nombres d’ondes avec l’énergie, la résonance entière
 risque d’être atteinte plus tôt pour des particules off-momentum. C’est ce que nous
allons maintenant vérifier.
risque d’être atteinte plus tôt pour des particules off-momentum. C’est ce que nous
allons maintenant vérifier.
A l’ESRF, la chromaticité est surcompensée à une valeur légèrement positive :  et
et
 . Pour différents écarts à l’énergie nominale, le point de fonctionnement va donc varier
avec
. Pour différents écarts à l’énergie nominale, le point de fonctionnement va donc varier
avec  suivant une courbe
suivant une courbe  (Fig. 3.32). En particulier, les résonances vont être
atteintes avec des amplitudes différentes par rapport au cas on momentum. D’autres résonances
vont également apparaître puisque d’autres régions de l’espace des fréquences vont être
explorées.
(Fig. 3.32). En particulier, les résonances vont être
atteintes avec des amplitudes différentes par rapport au cas on momentum. D’autres résonances
vont également apparaître puisque d’autres régions de l’espace des fréquences vont être
explorées.
|
|
Les cartes en fréquence ont été tracées en balayant à la fois les ouvertures dynamiques positive
et négative en  pour des écarts à l’énergie nominale de
pour des écarts à l’énergie nominale de  ,
,  et
et  (Fig. 3.33).
Nous allons donner une brève description des cartes en fréquence et ouvertures dynamiques
(plusieurs nouvelles résonances apparaissent cf. Tab. 3.10) :
(Fig. 3.33).
Nous allons donner une brève description des cartes en fréquence et ouvertures dynamiques
(plusieurs nouvelles résonances apparaissent cf. Tab. 3.10) :
 L’acceptance dynamique diminue (mais reste encore importante). Aussi bien
pour les positions
L’acceptance dynamique diminue (mais reste encore importante). Aussi bien
pour les positions  positives que négatives, l’ouverture dynamique est fortement
marquée par des résonances (présences d’îles importantes) qui se traduit par des bords
irréguliers et des protubérances.
positives que négatives, l’ouverture dynamique est fortement
marquée par des résonances (présences d’îles importantes) qui se traduit par des bords
irréguliers et des protubérances.
La carte en fréquence est maintenant vraiment irrégulière au-delà de la résonance entière : la diffusion est élevée. Que dira-t-on s’il y a quelques défauts qui viennent perturber la dynamique ? Il y aura augmentation de la diffusion des orbites.
 L’ouverture dynamique se détériore de plus en plus au-delà de la résonance
entière qui est atteinte à amplitude de plus en plus faible de par le glissement du point
de fonctionnement.
L’ouverture dynamique se détériore de plus en plus au-delà de la résonance
entière qui est atteinte à amplitude de plus en plus faible de par le glissement du point
de fonctionnement.
 On observe un trou dans l’ouverture dynamique au voisinage de la résonance
entière (comportement hyperbolique) qui est atteinte très tôt. Si l’on ne considère que
l’acceptance avant cette résonance, alors elle est très petite :
On observe un trou dans l’ouverture dynamique au voisinage de la résonance
entière (comportement hyperbolique) qui est atteinte très tôt. Si l’on ne considère que
l’acceptance avant cette résonance, alors elle est très petite :  mm,
mm,  mm
par rapport à la chambre à vide. On observe nettement la « nocivité » de la résonance
entière.
mm
par rapport à la chambre à vide. On observe nettement la « nocivité » de la résonance
entière.
|
 On note l’apparition d’une nouvelle résonance d’ordre 6. La résonance entière n’est
plus atteinte. La carte en fréquence « se déplie ». La dynamique est dominée par la résonance
d’ordre 5,
On note l’apparition d’une nouvelle résonance d’ordre 6. La résonance entière n’est
plus atteinte. La carte en fréquence « se déplie ». La dynamique est dominée par la résonance
d’ordre 5,  .
.
 L’ouverture dynamique est plus grande qu’à 1% (il n’y a plus la résonance entière).
La carte est presque plate. Au voisinage de la résonance
L’ouverture dynamique est plus grande qu’à 1% (il n’y a plus la résonance entière).
La carte est presque plate. Au voisinage de la résonance  , la dynamique est
perturbée.
, la dynamique est
perturbée.
 L’ouverture dynamique est très grande car à faible amplitude, il y a peu de
résonances. Seuls les bords sont fortement irréguliers et incisés par les résonances.
Paradoxalement, la dynamique est plus régulière dans ce cas que pour les particules on
momentum.
L’ouverture dynamique est très grande car à faible amplitude, il y a peu de
résonances. Seuls les bords sont fortement irréguliers et incisés par les résonances.
Paradoxalement, la dynamique est plus régulière dans ce cas que pour les particules on
momentum.|
|
La dynamique est très altérée par les résonances qui détériorent fortement la dynamique (diffusion élevée). Les deux résonances principales sont la résonance d’ordre 5 au voisinage de laquelle est faite l’injection et la résonance entière qui va réduire l’ouverture dynamique. Si l’on fait l’hypothèse que cette résonance ne peut pas être traversée, alors l’acceptance dynamique peut limiter la durée de vie du faisceau comme nous allons le voir.
Dans un anneau de stockage, le faisceau a une durée de vie finie du fait des différents mécanismes de perte : excitation quantique, diffusions simples ou multiples entre les électrons, diffusions sur les atomes du gaz résiduel. Pour les sources de lumière de troisième génération (faible émittance) comme l’ESRF, la durée de vie est déterminée principalement par la durée de vie Touschek que nous allons définir. Lors d’une collision entre deux électrons d’un même paquet, une partie de leurs moments transverses est transférée en moments longitudinaux. Si ces transferts sont plus grands que l’acceptance en énergie donnée par le système RF, les électrons sont perdus après la collision. De plus, les électrons diffusés qui restent à l’intérieur de l’acceptance longitudinale peuvent aussi être perdus dans le plan transverse dû à la limite de l’ouverture physique ou dynamique pour l’écart en énergie considéré.
La durée de vie Touschek a été calculée en mode multipaquets et en mode faible nombre de paquets qui sont deux des principaux modes de fonctionnement de l’ESRF. Les paramètres adoptés pour les calculs avec le logiciel BETA sont donnés par le tableau 3.11.
Les calculs ont été faits en approximation linéaire et nonlinéaire et sont présentés dans le
tableau 3.12. Dans chaque cas, nous avons pris comme longueur de paquet la longueur
naturelle  à courant nul ; en fonctionnement réel, le paquet s’allonge, e.g. d’un facteur
3 à 16 mA par paquet et la durée de vie est environ trois fois plus grande (Besnier,
Laclare, Limborg, 1996). En approximation linéaire, la durée de vie Touschek (
à courant nul ; en fonctionnement réel, le paquet s’allonge, e.g. d’un facteur
3 à 16 mA par paquet et la durée de vie est environ trois fois plus grande (Besnier,
Laclare, Limborg, 1996). En approximation linéaire, la durée de vie Touschek ( ) est
donnée par la formule classique (voir par exemple Le Duff, 1995 ou chap. XXX de Bruck,
1966) :
) est
donnée par la formule classique (voir par exemple Le Duff, 1995 ou chap. XXX de Bruck,
1966) :
 | =  D(ξ), ξ = D(ξ), ξ =  2 2 | (3.2) | |
| D(ξ) | =   |
 ,
,  les dimensions transverses et
les dimensions transverses et 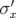 la divergence horizontale du faisceau,
la divergence horizontale du faisceau,  l’acceptance en énergie de la machine,
l’acceptance en énergie de la machine,  m le rayon classique de l’électron,
m le rayon classique de l’électron,  le
nombre d’électrons par paquet.
le
nombre d’électrons par paquet.
Pour le calcul dit nonlinéaire, nous avons pris en compte l’orbite fermée chromatique nonlinéaire et la dépendance en l’énergie des fonctions optiques. Pour une description détaillée, le lecteur peut se reporter à la méthode développée pour SOLEIL (Nadji et al., 1997).
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
De manière générale, la durée de vie Touschek est limitée soit par l’acceptance physique, soit par l’acceptance dynamique ou soit par l’acceptance en tension RF. Pour ces calculs, nous avons inclus les dimensions de l’ouverture dynamique off momentum (cf. Fig. 3.35).
A 8 MV, nous constatons que la tension RF est limitative ( ) alors qu’à 12 MV
c’est l’acceptance physique (
) alors qu’à 12 MV
c’est l’acceptance physique ( ) et même l’acceptance dynamique si toute la dynamique
au-delà de la résonance entière est négligée.
) et même l’acceptance dynamique si toute la dynamique
au-delà de la résonance entière est négligée.
|
|
Dans tous les cas, il est absolument nécessaire prendre en compte le second ordre pour calculer la durée de vie Touschek. En effet, au-delà de 8 MV, les résultats obtenus par les calculs linéaire et nonlinéaire sont très différents ; cette différence atteint un facteur 3 à 12 MV (cf. Fig. 3.34).
Le second jeu hexapolaire est une tentative d’optimisation du point de
fonctionnement précédent (pas d’améliorations expérimentales notables sauf à fort
courant18).
Seule la pente à l’origine de la courbe en fréquence est modifiée de  à
à 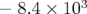 en
modifiant les réglages hexapolaires. Cependant la dynamique du faisceau est complètement modifiée
(cf. Fig. 3.36). Nous nous attarderons sur la comparaison des deux optiques.
en
modifiant les réglages hexapolaires. Cependant la dynamique du faisceau est complètement modifiée
(cf. Fig. 3.36). Nous nous attarderons sur la comparaison des deux optiques.
|
|
L’ouverture dynamique (cf. Fig. 3.36) est encore plus grande que celle obtenue pour le premier
réglage (cf. Fig. 3.28) : ![[− 80,45]y=0 × [− 15,15]x=0](these1412x.png) mm, plus régulière mais elle est
toujours surestimée. Comme précédemment, la carte en fréquence (Fig. 3.37, voir aussi les
cartes en couleur B.11) présente un repliement et peut être scindée en deux parties
(Fig. 3.38) :
mm, plus régulière mais elle est
toujours surestimée. Comme précédemment, la carte en fréquence (Fig. 3.37, voir aussi les
cartes en couleur B.11) présente un repliement et peut être scindée en deux parties
(Fig. 3.38) :
![[− 30, 20] × [− 8, 8]](these1413x.png) mm dans l’espace des configurations, avec un
glissement des nombres d’ondes très faible (
mm dans l’espace des configurations, avec un
glissement des nombres d’ondes très faible ( ). Cette partie est
extrêmement régulière et pratiquement exempte de résonances avec peu de diffusion.
). Cette partie est
extrêmement régulière et pratiquement exempte de résonances avec peu de diffusion.
 ne soit
jamais atteinte, la résonance d’ordre 5,
ne soit
jamais atteinte, la résonance d’ordre 5,  est déjà fortement
excitée pour une machine idéale puisqu’elle capture toutes les particules de conditions
initiales
est déjà fortement
excitée pour une machine idéale puisqu’elle capture toutes les particules de conditions
initiales ![x ∈ [− 74, − 42] ∪ [32, 35]](these1417x.png) mm.
mm.De manière générale pour ce réglage, la dynamique est moins « compliquée » et beaucoup plus
stable. Le glissement des nombres d’ondes avec l’amplitude est plus faible, si bien que la résonance
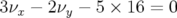 est atteinte à une amplitude
est atteinte à une amplitude  mm soit aussi grande que l’ouverture
physique (
mm soit aussi grande que l’ouverture
physique (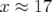 mm pour le premier réglage hexapolaire).
mm pour le premier réglage hexapolaire).
|
|
|
|
Deux orbites particulières ont été intégrées pour illustrer la diffusion au voisinage d’une résonance dans une zone de mouvement régulier et irrégulier (Fig. 3.40-a,b) :
La première orbite (O1) correspond aux conditions initiales  mm avec
pour nombres d’ondes initiaux
mm avec
pour nombres d’ondes initiaux 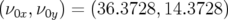 . L’intégration est réalisée sur 1
million de tours, les fréquences sont recalculées tous les 1 000 tours ; la particule oscille rapidement
transversalement à la résonance
. L’intégration est réalisée sur 1
million de tours, les fréquences sont recalculées tous les 1 000 tours ; la particule oscille rapidement
transversalement à la résonance  et lentement longitudinalement (voir aussi
Fig. 3.39).
et lentement longitudinalement (voir aussi
Fig. 3.39).
|
|
La seconde orbite (O2) est perdue au bout de 38 026 tours de l’anneau. Ses conditions initiales
en amplitudes et en fréquences sont 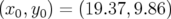 mm et
mm et 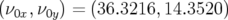 ,
soit au voisinage de la résonance
,
soit au voisinage de la résonance  . La particule y reste environ 15 000
tours avant de diffuser rapidement L’évolution de la partie fractionnaire des nombres d’ondes avec le
nombre de tours est donné par la figure 3.40-b.
. La particule y reste environ 15 000
tours avant de diffuser rapidement L’évolution de la partie fractionnaire des nombres d’ondes avec le
nombre de tours est donné par la figure 3.40-b.
Comme pour le premier réglage, les valeurs réduites des chromaticités sont légèrement positives
( et
et  ). Le glissement des nombres d’ondes avec l’énergie
). Le glissement des nombres d’ondes avec l’énergie 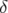 est illustré par la
figure 3.42.
est illustré par la
figure 3.42.
Les cartes en fréquence ont été tracées pour des écarts à l’énergie nominale compris entre
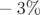 et
et 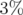 (Fig. 3.41) en considérant toujours une machine parfaite.
(Fig. 3.41) en considérant toujours une machine parfaite.
|
|
L’ouverture dynamique diminue avec  (cf. Fig. 3.43) ; cette diminution est plus importante
pour des écarts à l’énergie positifs.
(cf. Fig. 3.43) ; cette diminution est plus importante
pour des écarts à l’énergie positifs.
L’allure et le repliement des cartes varient beaucoup avec  . Pour de grands écarts en énergie,
les cartes sont pratiquement « plates » ; notons cependant que pour
. Pour de grands écarts en énergie,
les cartes sont pratiquement « plates » ; notons cependant que pour  , les nombres d’ondes
diminuent avec l’amplitudes (distances au centre du faisceau) alors que pour
, les nombres d’ondes
diminuent avec l’amplitudes (distances au centre du faisceau) alors que pour 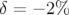 , ils
augmentent avec l’amplitude.
, ils
augmentent avec l’amplitude.
|
|
Pour 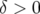 , la résonance d’ordre 5,
, la résonance d’ordre 5,  est atteinte beaucoup plus tôt, et surtout,
la résonance
est atteinte beaucoup plus tôt, et surtout,
la résonance  , systématique d’ordre 4 et destructive ici, limite la dynamique ; ce
qui explique la diminution drastique de plus de 50 % de l’ouverture dynamique entre
0% et +2%. Par contre au-delà de +3%, la résonance
, systématique d’ordre 4 et destructive ici, limite la dynamique ; ce
qui explique la diminution drastique de plus de 50 % de l’ouverture dynamique entre
0% et +2%. Par contre au-delà de +3%, la résonance  n’est plus destructive
pour une machine idéale : l’ouverture dynamique est de nouveau plus grande (frontière
2.3%).
n’est plus destructive
pour une machine idéale : l’ouverture dynamique est de nouveau plus grande (frontière
2.3%).
Pour  , de nouvelles résonances de couplages (Tab. 3.13) apparaissent de par le
déplacement du point de fonctionnement avec l’énergie.
, de nouvelles résonances de couplages (Tab. 3.13) apparaissent de par le
déplacement du point de fonctionnement avec l’énergie.
|
Comme annoncé précédemment, les résonances 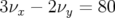 et
et  ont une grande
amplitude qu’il faudrait essayer de réduire pour améliorer l’ouverture dynamique pour
ont une grande
amplitude qu’il faudrait essayer de réduire pour améliorer l’ouverture dynamique pour
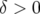 .
.
Pour 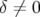 , l’extension des cartes en fréquence est plus importante que pour l’énergie
nominale. D’autres résonances vont alors dominer dans la dynamique aux différentes
amplitudes.
, l’extension des cartes en fréquence est plus importante que pour l’énergie
nominale. D’autres résonances vont alors dominer dans la dynamique aux différentes
amplitudes.
L’acceptance dynamique diminue avec 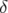 , mais dans le pire des cas elle reste comparable avec
l’acceptance physique.
, mais dans le pire des cas elle reste comparable avec
l’acceptance physique.
La surcompensation de la chromaticité a l’inconvénient majeur de compliquer l’optimisation, puisque les points de fonctionnement dépendent fortement de l’énergie de la particule. Idéalement, il faudrait pouvoir optimiser la dynamique aux différentes énergies.
La durée de vie Touschek est calculée de la même manière que pour le premier réglage hexapolaire. Les résultats sont rassemblés dans le tableau 3.14 (voir aussi les figures 3.44-a et b).
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
En comparant les durées de vie Touschek obtenues pour les deux réglages hexapolaires de
l’ESRF (Fig. 3.34 et Fig. 3.44), nous constatons que le second réglage est meilleur. Ce résultat se
comprend bien si l’on se rappelle que la dynamique off momentum du premier réglage est fortement
marquée par la résonance entière  , si bien qu’il faut prendre en compte dans les calculs
l’ouverture dynamique off momentum qui est alors le facteur limitatif. Ces résultats tendraient à
corroborer les mesures expérimentales. Il faut toutefois reconnaître que les durées de vie mesurées
sont bien plus faibles.
, si bien qu’il faut prendre en compte dans les calculs
l’ouverture dynamique off momentum qui est alors le facteur limitatif. Ces résultats tendraient à
corroborer les mesures expérimentales. Il faut toutefois reconnaître que les durées de vie mesurées
sont bien plus faibles.
Pour le point de fonctionnement 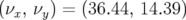 la dynamique du deuxième jeu
hexapolaire semble être la plus « stable » : peu de résonances au voisinage du point de
fonctionnement, faible diffusion, ouverture dynamique plus grande que l’acceptance physique jusqu’à
la dynamique du deuxième jeu
hexapolaire semble être la plus « stable » : peu de résonances au voisinage du point de
fonctionnement, faible diffusion, ouverture dynamique plus grande que l’acceptance physique jusqu’à
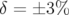 .
.
Pour le premier jeu hexapolaire, nous constatons qu’il y a plus de résonances qui induisent une diffusion globalement plus importante. La dynamique est fortement perturbée par la résonance entière. Si nous faisons l’hypothèse que celle-ci limite l’ouverture dynamique, la durée de vie Touschek serait alors réduite.
|
|
Le point de fonctionnement historique de l’ESRF avait pour nombres d’ondes
 . Une étude a également été faite pour comprendre pourquoi les
performances de l’anneau étaient bien trop faibles pour les deux réglages hexapolaires
nominaux. En fait la dynamique est globalement plus mauvaise, car la résonance entière, plus
proche du point de fonctionnement, est atteinte à plus faible amplitude. Les cartes en
fréquence pour les deux réglages hexapolaires (cf. Fig. 3.45) sont peuplées de résonances
avec une diffusion des orbites très élevée et des ouvertures dynamiques petites. Pour le
premier jeu hexapolaire (cf. Fig. 3.45-a), la dynamique est « catastrophique » : le point de
fonctionnement est trop proche des résonances entières
. Une étude a également été faite pour comprendre pourquoi les
performances de l’anneau étaient bien trop faibles pour les deux réglages hexapolaires
nominaux. En fait la dynamique est globalement plus mauvaise, car la résonance entière, plus
proche du point de fonctionnement, est atteinte à plus faible amplitude. Les cartes en
fréquence pour les deux réglages hexapolaires (cf. Fig. 3.45) sont peuplées de résonances
avec une diffusion des orbites très élevée et des ouvertures dynamiques petites. Pour le
premier jeu hexapolaire (cf. Fig. 3.45-a), la dynamique est « catastrophique » : le point de
fonctionnement est trop proche des résonances entières  et
et 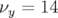 , résonances qui sont
les premières à éviter lorsque l’on choisi le point de fonctionnement d’un accélérateur.
L’auteur est perplexe et ne comprend pas quels critères ont pu amener à ce choix. Le
point de fonctionnement actuel de l’ESRF, choisi à la suite de discussion avec le groupe
faisceau du projet SOLEIL, diffère uniquement par l’éloignement de la résonance entière
, résonances qui sont
les premières à éviter lorsque l’on choisi le point de fonctionnement d’un accélérateur.
L’auteur est perplexe et ne comprend pas quels critères ont pu amener à ce choix. Le
point de fonctionnement actuel de l’ESRF, choisi à la suite de discussion avec le groupe
faisceau du projet SOLEIL, diffère uniquement par l’éloignement de la résonance entière
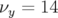 .
.
La Source de Lumière Avancée du Ernest Orlando Lawrence Berkeley National Laboratory (Advanced Light Source, ALS [3] et [4]) a eu sa première lumière en 1993. Mise en service juste après l’ESRF, son énergie est plus basse, 1.5–1.9 GeV contre 6 GeV, elle est donc plus optimisée pour les rayons UV et « X-mou ».
Une première étude théorique de l’ALS avec l’Analyse en Fréquence a été réalisée dès 1993 par Dumas et Laskar. Le point de fonctionnement actuel de l’ALS est très voisin de celui proposés en 1996 par Laskar et Robin.
L’ALS a une périodicité 12, sa maille est construite sur une structure triple bend achromat (TBA)
avec symétrie centrale (cf. fonctions optiques Fig. 3.46). Les nonlinéarités sont introduites par les
deux uniques familles d’hexapôles utilisées pour corriger la chromaticités à des valeurs légèrement
positives, 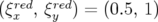 (cf. Tab. 3.15). Les logiciels DESPOT [42] et TRACY2 [11] ont été
utilisés pour intégrer les particules « test » sur deux fois 1 000 tours, i.e. deux fois un vingtième du
temps d’amortissement de l’anneau.
(cf. Tab. 3.15). Les logiciels DESPOT [42] et TRACY2 [11] ont été
utilisés pour intégrer les particules « test » sur deux fois 1 000 tours, i.e. deux fois un vingtième du
temps d’amortissement de l’anneau.
Nous avons commencé par étudier une maille parfaite de l’ALS. L’anneau a alors sa périodicité 12
permettant de réduire grandement le nombre de résonances permises. Il s’ensuit que l’ouverture
dynamique est très grande ![[0, 22] × [0, 10]](these1515x.png) mm alors qu’expérimentalement, le faisceau commence
a être perdu dès l’amplitude
mm alors qu’expérimentalement, le faisceau commence
a être perdu dès l’amplitude 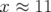 mm (cf. Fig. 3.47).
mm (cf. Fig. 3.47).
Contrairement autres machines étudiées, la carte en fréquence est très simple sans repliement : le
point de fonctionnement 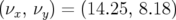 est le coin supérieur droit de la carte en
fréquence 3.47. Le bord supérieur (respectivement inférieur) de la carte correspond à la variation
des nombres d’ondes avec l’amplitude pour
est le coin supérieur droit de la carte en
fréquence 3.47. Le bord supérieur (respectivement inférieur) de la carte correspond à la variation
des nombres d’ondes avec l’amplitude pour  (respectivement
(respectivement  ). L’ensemble des
résonances principales identifiées est donné par la figure 3.48. Les deux résonances les
plus néfastes pour la dynamique sont la résonance entière
). L’ensemble des
résonances principales identifiées est donné par la figure 3.48. Les deux résonances les
plus néfastes pour la dynamique sont la résonance entière  et la résonance de
couplage19
et la résonance de
couplage19
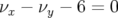 . Loin du point de fonctionnement, les largeurs de résonance se recouvrent
induisant des mouvements de nature chaotique avec une diffusion élevée. C’est également vrai sur
les bords de l’ouverture dynamique (cf. Fig. 3.47, voir aussi la carte en couleur B.12).
. Loin du point de fonctionnement, les largeurs de résonance se recouvrent
induisant des mouvements de nature chaotique avec une diffusion élevée. C’est également vrai sur
les bords de l’ouverture dynamique (cf. Fig. 3.47, voir aussi la carte en couleur B.12).
|
|
Une maille plus réaliste de l’ALS peut être modélisée en prenant en compte les erreurs de gradients déduites de l’analyse de la matrice-réponse20 non couplée (Robin, Safranek et Decking, 1998 et 1999) en utilisant le programme LOCO (Safranek, 1997). Les matrices-réponse de l’anneau sont mesurées chaque semaine pour déterminer si l’optique de la machine a changé ou non de manière significative. Les défauts mesurés sur les forces quadripolaires correspondent en moyenne à des variations de 0.36% rms des valeurs nominales pour les quadripôles défocalisants et 0.2% rms pour les quadripôles focalisant ; ces variations sont loin d’être négligeables et vont induire de profondes modifications de la dynamique.
Les nouvelles carte en fréquence et ouverture dynamique sont données par la figure 3.49 (voir
aussi la carte en couleur B.13) : la dynamique globale est complètement modifiée, la
12-périodicité brisée, donc la condition de résonance est beaucoup moins sévère. En particulier la
résonance entière  est excitée par les défauts quadripolaires comme la théorie le
prévoit (voir par exemple chap. II in Accelerator Physics, Lee, 1998) et toutes les orbites
dans son voisinage et à plus grandes amplitudes sont instables (quelques centaines de
tours).
est excitée par les défauts quadripolaires comme la théorie le
prévoit (voir par exemple chap. II in Accelerator Physics, Lee, 1998) et toutes les orbites
dans son voisinage et à plus grandes amplitudes sont instables (quelques centaines de
tours).
Les nouvelles dimensions de l’ouverture dynamique sont maintenant ![[0, 12] × [0, 8]](these1532x.png) mm.
L’ouverture dynamique horizontale est maintenant plus petite que l’ouverture
physique (cf. Tab. 3.15). En effet dans le plan horizontal, elle est limitée par
la résonance de couplage
mm.
L’ouverture dynamique horizontale est maintenant plus petite que l’ouverture
physique (cf. Tab. 3.15). En effet dans le plan horizontal, elle est limitée par
la résonance de couplage  . Expérimentalement, en utilisant un
scraper21
horizontal ou en déplaçant le faisceau, nous retrouvons une ouverture dynamique similaire (Decking
et Robin, 1999).
. Expérimentalement, en utilisant un
scraper21
horizontal ou en déplaçant le faisceau, nous retrouvons une ouverture dynamique similaire (Decking
et Robin, 1999).
|
|
L’extension de la carte en fréquence est réduite verticalement d’un facteur deux. Les résonances
d’ordre 5 sont excitées :  ,
,  et
et 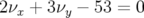 , ce sont
des résonances non permises par la 12-périodicité (cf. Fig. 3.51).
, ce sont
des résonances non permises par la 12-périodicité (cf. Fig. 3.51).
De manière générale, la zone de stabilité est réduite au voisinage du point de fonctionnement. Toutes les particules ayant un indice de diffusion inférieur à moins six seront sans doute perdues si l’on intègre les trajectoires plus longtemps.
Le modèle de l’ALS peut encore être affiné en introduisant du couplage modélisé par des erreurs de gradients de quadripôles tournés. Ces défauts sont également déduits des mesures de matrices-réponses couplées (Robin, Safranek, Decking, 1999) pour avoir un couplage effectif de 1%. Les écarts en valeur rms sont de l’ordre de 0.3%.
Il apparaît clairement à la lecture de la nouvelle carte en fréquence (cf. Fig. 3.50 à comparer
avec Fig. 3.49, voir aussi la carte en couleur B.14) que la dynamique est encore plus instable : la
diffusion est plus élevée, les largeurs de résonances sont plus grandes ; la majorité des orbites situées
sur la carte en fréquence à gauche de la résonance d’ordre 5, 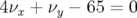 ont un coefficient
de diffusion très élevé (
ont un coefficient
de diffusion très élevé ( ) : les lignes de résonances sont moins lisibles dénotant la
superposition des largeurs de résonances. Les particules peuvent plus facilement et rapidement
diffuser, toute structure régulière est perdue. En fonctionnement réel, la dynamique du faisceau de
l’ALS est certainement encore moins stable : en effet d’autres défauts magnétiques ainsi que
l’influence de la dynamique longitudinale ont été négligés dans cette étude. La résonance
) : les lignes de résonances sont moins lisibles dénotant la
superposition des largeurs de résonances. Les particules peuvent plus facilement et rapidement
diffuser, toute structure régulière est perdue. En fonctionnement réel, la dynamique du faisceau de
l’ALS est certainement encore moins stable : en effet d’autres défauts magnétiques ainsi que
l’influence de la dynamique longitudinale ont été négligés dans cette étude. La résonance
 peut être considérée comme limitant l’ouverture dynamique (cf.
Fig. 3.51).
peut être considérée comme limitant l’ouverture dynamique (cf.
Fig. 3.51).
|
|
La dynamique off momentum de l’ALS n’a pas été étudiée de manière exhaustive. Elle a pourtant
un rôle déterminant sur la durée de vie du faisceau. Les figures 3.52 représentent la variation des
nombres d’ondes en fonction de l’énergie,  ainsi que la variation du point de
fonctionnement dans l’espace des fréquences. Les cartes en fréquence (Fig. 3.53) ont été
tracées pour une machine idéale 12-périodique et pour des écarts à l’énergie nominale
ainsi que la variation du point de
fonctionnement dans l’espace des fréquences. Les cartes en fréquence (Fig. 3.53) ont été
tracées pour une machine idéale 12-périodique et pour des écarts à l’énergie nominale
 . En s’appuyant sur la comparaison des cartes en fréquence 3.47, 3.49 et 3.50
le lecteur pourra aisément prédire l’évolution des cartes en fréquence 3.53 si les défauts
magnétiques mesurés sont incorporés au modèle.
. En s’appuyant sur la comparaison des cartes en fréquence 3.47, 3.49 et 3.50
le lecteur pourra aisément prédire l’évolution des cartes en fréquence 3.53 si les défauts
magnétiques mesurés sont incorporés au modèle.
Nous donnons quelques indices de lecture de ces cartes en fréquence. L’introduction des défauts magnétiques ne peut que détériorer la dynamique du faisceau. S’ils sont suffisamment élevés, comme nous l’avons vu, alors la 12-périodicité de l’anneau est brisée. Les résonances non permises vont en particulier être plus excitées. Ceci se traduit par l’augmentation des largeurs des résonances et une plus grande probabilité de recouvrement des résonances, siège du chaos. Cette détérioration globale de la dynamique est d’autant plus importante que les particules oscillent avec de plus grandes amplitudes.
Une des caractéristiques de l’Analyse en Fréquence est sa capacité de prédiction lorsque l’on lit
une carte en fréquence. Par exemple, la dynamique off momentum de l’ALS est déjà, pour une
machine idéale, fortement marquée par le nœud entre les résonances  ,
,
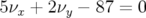 et
et  (cf. carte 3.53 pour
(cf. carte 3.53 pour  ) et le nœud entre les
résonances
) et le nœud entre les
résonances 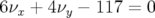 ,
,  et
et  (cf. carte pour
(cf. carte pour
 ). Toute la dynamique en leur voisinage respectif et aux amplitudes plus élevées sera
instable pour la machine réelle.
). Toute la dynamique en leur voisinage respectif et aux amplitudes plus élevées sera
instable pour la machine réelle.
|
|
|
|
L’ALS est une machine relativement « simple ». Les cartes en fréquence sont « plates » sans repliement. Il n’y a que deux familles d’hexapôles utilisées pour ajuster la chromaticité. En contrepartie, si la dynamique est très nonlinéaire, le seul recourt est de déplacer le point de fonctionnement dans une région du diagramme des résonances vierge de résonance. Il n’existe pas de famille hexapolaire pour réduire les largeurs des résonances. L’Analyse en Fréquence permet de mettre en évidence clairement toutes les résonances principales, en particulier les résonances de couplage (couplées) non vues ni étudiées dans les processus d’optimisation traditionnels.
Pour étudier l’influence des défauts magnétiques sur la dynamique globale du faisceau, on procède habituellement par tirages aléatoires de jeux de défauts (méthodes statistiques, Méthode de Monte Carlo). Cette méthode est très coûteuse en termes de temps de calcul mais est la seule possible lorsque la machine n’est pas encore construite.
La méthode que nous avons retenue est d’utiliser les défauts magnétiques mesurés sur l’anneau de stockage — uniquement possible si la machine est en fonctionnement —. Cette méthode ne nécessite qu’un seul jeu de défaut et donne des résultats très satisfaisants comme nous l’avons vu pour l’ALS
Les cartes en fréquence calculées pour l’ALS permettent d’expliquer un certain nombre de résultats expérimentaux, en particulier l’efficacité de l’injection ; la prise en compte de la dynamique off momentum devrait permettre d’obtenir des durées de vie s’approchant des mesures expérimentales. Les dimensions de l’ouverture dynamique déduite de cette étude sont compatibles avec les mesures sur l’anneau. Ce dernier point est également remarquable, car généralement l’écart entre théorie et expérience est souvent supérieur à un facteur deux sur la plupart des sources de lumière (e.g. à l’ESRF). D’autres résultats plus spectaculaires ont été obtenus sur l’ALS. Je renvoie le lecteur à la partie expérimentale de cette thèse (chapitre suivant).
Je voudrais insister sur le fait que ces premiers résultats n’ont été possibles que parce qu’au préalable un long travail de caractérisation de la machine avait été réalisé. L’ALS est un anneau de stockage équipé d’un grand nombre d’outils de diagnostic prévus dès la construction : moniteurs de position tour par tour, aimants rapides permettant de perturber le faisceau sur un seul tour de machine, perturbateurs horizontal et vertical. Ce sont les « yeux et les oreilles » du physicien des accélérateurs. Il est ainsi possible d’explorer la dynamique du faisceau. A cela, il convient d’ajouter que chaque année, de nombreuses heures ont été et sont encore réservées uniquement à l’amélioration de la modélisation de l’anneau.