Nous avons vu qu’il est difficile de modéliser correctement la dynamique réelle d’un anneau de stockage, car il faut être capable d’identifier les principales résonances pour essayer ensuite de limiter leur influence. Ce travail est délicat si bien que souvent l’écart entre les performances escomptées et réelles pour une machine donnée peut atteindre plus d’un facteur deux. L’Analyse en Fréquence est ici utilisée pour réaliser ce lien entre théorie et expérience.
Dans le chapitre précédent, nous avons calculé des cartes en fréquence de l’ALS considérée soit comme une machine idéale avec sa 12-périodicité, soit comme une machine réelle, i.e. incorporant les défauts magnétiques mesurés. Pour mémoire, les nombres d’ondes choisis correspondent au point de fonctionnement nominal de l’ALS, tout comme les chromaticités qui sont légèrement surcompensées. Les deux cartes en fréquence obtenues (voir figure 4.1) mettent en évidence combien la dynamique est sensible aux défauts magnétiques : leur introduction réduit d’un facteur deux l’extension spatiale de la carte en fréquence, les largeurs de résonances sont plus importantes, de nouvelles droites de résonance apparaissent et la stabilité du faisceau est fortement détériorée. Les performances déduites de ce nouveau modèle sont maintenant beaucoup plus proches de l’expérience. L’ultime étape est désormais de pouvoir comparer notre modélisation de l’ALS directement avec la machine en fonctionnement.
Les résultats que nous avons obtenus s’inscrivent dans une longue collaboration entre J. Laskar et le groupe accélérateur de D. Robin à Berkeley. Une première étude théorique de l’ALS avec l’Analyse en Fréquence a été réalisée dès 1993 (Dumas et Laskar, 1993). Les réglages magnétiques utilisés actuellement sur l’ALS sont très voisins de ceux proposés en 1996 (Laskar et Robin, 1996) et avaient permis d’améliorer significativement les performances machine (temps d’injection du faisceau dans l’anneau, durée de vie). Cependant des écarts encore importants subsistaient entre la théorie et l’expérience. Un long et délicat travail de caractérisation des défauts magnétiques expérimentaux de chaque type d’aimant a été entrepris jusqu’à ce jour.
Cette étape préliminaire est fondamentale et est une condition sine qua non
avant toute tentative d’étude de la dynamique nonlinéaire. Elle a permis d’obtenir
une calibration du modèle linéaire de l’ALS. Pour cela, les matrices-réponse
expérimentales1
sont analysées depuis de nombreuses années (Robin, Safranek et Decking, 1999) en utilisant le
programme LOCO (Safranek, 1997) que nous décrirons dans le chapitre 5. Dans cette analyse, tous
les gradients quadripolaires (naturels et induits dans les hexapôles) sont déterminés avec une
précision d’environ un millième. Après correction, les battements des fonctions 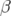 sont
relativement faibles, 1% et 2% respectivement dans les plans horizontal et vertical. De plus, le
programme LOCO a été récemment modifié pour permettre de modéliser le couplage à
partir des matrices-réponse de l’anneau en un temps de calcul non prohibitif (Steier,
2000).
sont
relativement faibles, 1% et 2% respectivement dans les plans horizontal et vertical. De plus, le
programme LOCO a été récemment modifié pour permettre de modéliser le couplage à
partir des matrices-réponse de l’anneau en un temps de calcul non prohibitif (Steier,
2000).
Les questions que l’on se pose actuellement sont : quelle fiabilité accorder à ce modèle de
l’anneau ? Que se passe-t-il si nous modifions l’optique de la machine ? Quel est l’impact des
sections à faible fonction 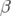 (low beta insertion straight sections), l’impact de l’introduction de
nouveaux éléments ? Par exemple, au mois d’août 2001, trois des trente-six dipôles (à 1.3 Tesla) de
l’ALS seront remplacés par des aimants supraconducteurs (à 5 Tesla). Comment améliorer les
performances de l’anneau aujourd’hui ?
(low beta insertion straight sections), l’impact de l’introduction de
nouveaux éléments ? Par exemple, au mois d’août 2001, trois des trente-six dipôles (à 1.3 Tesla) de
l’ALS seront remplacés par des aimants supraconducteurs (à 5 Tesla). Comment améliorer les
performances de l’anneau aujourd’hui ?
Pour commencer, il est important de rappeler, que le type de mesure que nous allons décrire étaient les premières de cette catégorie, si bien qu’un certain nombre de petites expériences préparatoires (calibration, réponse de l’électronique, écriture des routines de contrôles) ont été faites dès mon arrivée dans le groupe théorie de l’Advanced Light Source.
Deux outils fondamentaux ont permis de réaliser les mesures. Le premier consiste en un couple
d’aimants rapides capables de donner une impulsion au faisceau ; l’un délivre une impulsion
horizontale (H), l’autre une impulsion verticale (V). Chaque aimant a un temps de réponse de
600 ns, soit un temps inférieur à celui mis par le faisceau pour faire un tour de machine
(660 ns). Les deux aimants synchronisés permettent d’imprimer au faisceau des conditions
initiales  . Le second outil est un jeu de deux moniteurs de position (BPM : Beam
Position Monitor) tour par tour. Chaque BPM peut stocker 1 024 données consécutives et
est synchronisé avec les aimants rapides. Les deux BPM ont été choisis de manière à
avoir un bon rapport signal-sur-bruit respectivement dans le plan horizontal et vertical.
Les amplitudes données aux faisceaux restent dans la gamme linéaire de réponse des
BPM2 .
Il est ainsi possible d’enregistrer la position du faisceau pendant les 1 024 premiers tours après
l’impulsion.
. Le second outil est un jeu de deux moniteurs de position (BPM : Beam
Position Monitor) tour par tour. Chaque BPM peut stocker 1 024 données consécutives et
est synchronisé avec les aimants rapides. Les deux BPM ont été choisis de manière à
avoir un bon rapport signal-sur-bruit respectivement dans le plan horizontal et vertical.
Les amplitudes données aux faisceaux restent dans la gamme linéaire de réponse des
BPM2 .
Il est ainsi possible d’enregistrer la position du faisceau pendant les 1 024 premiers tours après
l’impulsion.
Durant une expérience, l’anneau est rempli avec 40 paquets soit un huitième de l’anneau. Ce
nombre a été choisi pour permettre tout à la fois d’obtenir une résolution satisfaisante sur les BPM
et de ne pas avoir d’oscillation inter-paquets (phénomènes collectifs, champ de sillage, charge
d’espace). Le courant injecté est de  mA, soit environ
mA, soit environ  électrons.
électrons.
Pour chaque expérience, deux jeux de mesures sont réalisés. D’abord, la matrice-réponse est enregistrée pour permettre de calibrer ultérieurement le modèle linéaire. Ensuite, les données tour par tour sont collectées pour construire la carte en fréquence. Comme en théorie et par soucis de temps d’expérience, le pas d’incrément des tensions des aimants rapides est choisi suivant une loi en racine carrée, ce qui permet d’obtenir des points espacés régulièrement dans l’espace des fréquences. Le temps d’acquisition est de 20 secondes pour chaque point (principalement dû à la réponse de l’électronique et à la bande passante du réseau), soit environ 4 heures pour une carte en fréquence complète.
Pour la première expérience, nous nous sommes placés dans les conditions de fonctionnement
standard en ce qui concerne les nombres d’ondes et les chromaticités (cf. Tab. 4.1). L’optique
linéaire a été mesurée et ajustée de telle manière à être aussi proche que possible d’une
symétrie 12. Les battements de fonctions  sont de l’ordre de 2–3%, le couplage est de
1%.
sont de l’ordre de 2–3%, le couplage est de
1%.
|
|
L’étalonnage des aimants rapides avait antérieurement été réalisé :  (H) et
(H) et
 (V).
(V).
Avant de présenter les cartes en fréquence expérimentales, il est intéressant de dire quelques mots sur l’analyse des données expérimentales.
La principale différence entre les résultats théoriques que nous avons présentés jusqu’ici et les
mesures expérimentales tient dans le fait que nous observons non pas le mouvement d’un seul
électron mais du centroïde d’un paquet d’environ un milliard d’électrons. La dynamique d’un
paquet de particules est bien plus complexe à étudier, l’objectif étant d’extraire la dynamique
d’une particule individuelle. Le nouveau phénomène mis en cause est la décohérence du
faisceau3.
En effet, avant qu’une impulsion ne soit donnée, le faisceau est amorti. Juste après l’impulsion
(temps  ), les particules d’un paquet oscillent toutes avec pratiquement la même amplitude et la
même phase, on parle alors d’oscillations cohérentes. A cause de la dispersion des fréquences
avec l’amplitude, les particules vont avoir un mouvement bétatron avec des fréquences
d’oscillation également différentes. Petit à petit, les particules vont se déphaser les unes
par rapport aux autres (temps
), les particules d’un paquet oscillent toutes avec pratiquement la même amplitude et la
même phase, on parle alors d’oscillations cohérentes. A cause de la dispersion des fréquences
avec l’amplitude, les particules vont avoir un mouvement bétatron avec des fréquences
d’oscillation également différentes. Petit à petit, les particules vont se déphaser les unes
par rapport aux autres (temps  ). Au bout d’un temps suffisamment long dit temps
de décohérence, les phases des particules du paquet seront distribuées uniformément
sur l’intervalle
). Au bout d’un temps suffisamment long dit temps
de décohérence, les phases des particules du paquet seront distribuées uniformément
sur l’intervalle  ; il n’y a plus aucune cohérence des oscillations et l’amplitude
moyenne du faisceau, i.e. celle du centroïde, tend vers zéro. Ce processus est illustré par le
schéma 4.2 où le paquet est constitués de
; il n’y a plus aucune cohérence des oscillations et l’amplitude
moyenne du faisceau, i.e. celle du centroïde, tend vers zéro. Ce processus est illustré par le
schéma 4.2 où le paquet est constitués de  particules dont les amplitudes sont distribuées
selon une gaussienne autour de la valeur imprimée par l’aimant rapide. On a supposé
que le temps de décohérence est beaucoup plus court que les temps d’amortissement
tranverses du faisceau. La décohérence a deux origines principale : la dépendance nonlinéaire
des nombres d’ondes avec l’amplitude bétatron et la dépendance linéaire des nombres
d’ondes avec l’énergie (en première approximation) que nous allons décrire de manière
exhaustive.
particules dont les amplitudes sont distribuées
selon une gaussienne autour de la valeur imprimée par l’aimant rapide. On a supposé
que le temps de décohérence est beaucoup plus court que les temps d’amortissement
tranverses du faisceau. La décohérence a deux origines principale : la dépendance nonlinéaire
des nombres d’ondes avec l’amplitude bétatron et la dépendance linéaire des nombres
d’ondes avec l’énergie (en première approximation) que nous allons décrire de manière
exhaustive.
|
|
Une question légitime est de savoir quelle va être l’influence de la décohérence sur l’analyse des résultats, et en particulier sur les nombres d’ondes déterminés.
Le modèle que nous allons présenter est inspiré de la publication de Lee (1992), donnée lors du
Workshop on Nonlinear Problems In Accelerator Physics de Berlin. Ce modèle est bidimensionnel,
les particules sont supposées distribuées transversalement et longitudinalement suivant une loi de
Gauss et la variation des nombres d’ondes est supposée linéaire en l’écart en énergie  et
quadratique en l’amplitude, i.e. :
et
quadratique en l’amplitude, i.e. :
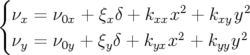 | (4.1) |
D’autres papiers ont été également très instructifs, voir par exemple Meller et al. (1987) et Ian (1990), ainsi que pour une formulation en variables actions-angles Shi et Ohnuma (1993).
Pour la présente formulation de la décohérence, les phénomènes suivants sont négligés :
Considérons une particule animée d’un mouvement bétatron (cf. chap. 1, Eq. 1.60). La variation du nombre d’ondes horizontal dépend de l’énergie de la particule à travers la chromaticité :
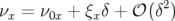 | (4.2) |
où  est la fonction chromaticité et
est la fonction chromaticité et 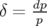 l’écart à l’énergie
nominale4.
l’écart à l’énergie
nominale4.
Si l’on appelle 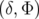 ses coordonnées
canoniques5
dans l’espace des phases longitudinal, alors dans l’approximation linéaire, la dynamique
longitudinale est gouvernée par le Hamiltonien (voir par exemple Lee, 1998) :
ses coordonnées
canoniques5
dans l’espace des phases longitudinal, alors dans l’approximation linéaire, la dynamique
longitudinale est gouvernée par le Hamiltonien (voir par exemple Lee, 1998) :
| H | =  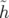 w0ηcδ2 − w0ηcδ2 −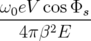 Φ2 Φ2 | ||
=  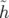 w0ηcδ2 + w0ηcδ2 +   Φ2 Φ2 | (4.3) |
 la fréquence synchrotron,
la fréquence synchrotron,  la fréquence de révolution,
la fréquence de révolution, 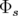 la
phase synchrone,
la
phase synchrone,  la tension radiofréquence effective,
la tension radiofréquence effective, 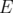 l’énergie de la particule,
l’énergie de la particule,
 ,
,  le nombre d’harmoniques et
le nombre d’harmoniques et 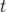 la variable indépendante.
la variable indépendante.
La trajectoire de phase est une ellipse d’équation dont nous choisissons d’écrire le paramétrage sous la forme :
 | (4.4) |
avec 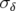 et
et  les dimensions d’équilibre des variables
les dimensions d’équilibre des variables 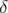 et
et 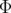 et
et  , l’aire de
l’ellipse de phase. Le glissement de la fréquence bétatron mesuré au n-ième tour s’écrit (Eq. 4.2 et
4.4) :
, l’aire de
l’ellipse de phase. Le glissement de la fréquence bétatron mesuré au n-ième tour s’écrit (Eq. 4.2 et
4.4) :
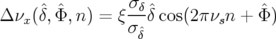 | (4.5) |
et le déphasage induit sur 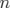 tours pour la particule considérée est par définition :
tours pour la particule considérée est par définition :
Δφx(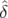 , ,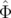 ,n) ,n) | = 2π ∫
0nΔν
x(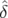 , ,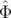 ,k) dk ,k) dk | ||
| soit en utilisant l’expression 4.5 : | |||
Δφx(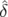 , , ,n) ,n) | = ξ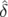  νs−1(sin(2πν
sn + νs−1(sin(2πν
sn + 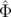 ) − sin( ) − sin(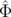 )) )) | ||
= ![[ −1 ]
2ξνs σδ sin(π νsn)](these1629x.png)  cos(πνsn + cos(πνsn +  ) ) | |||
= 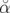  cos(πνsn + cos(πνsn +  ) avec ) avec 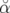 = = ![[ − 1 ]
2ξνs σδ sin(πνsn)](these1636x.png) | |||
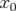 obéit à la
loi :
obéit à la
loi :
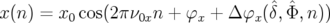 | (4.6) |
Le mouvement du centroïde d’un paquet de particules distribuées en
amplitude et phase selon une densité de probabilités 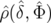 s’exprime alors
comme6 :
s’exprime alors
comme6 :
 | (4.7) |
Si les lois de distribution en amplitudes 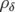 et en phases
et en phases  des particules sont des gaussiennes de
moyennes nulles et d’écart-types respectifs
des particules sont des gaussiennes de
moyennes nulles et d’écart-types respectifs 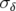 et
et 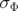 , alors la fonction de densité de probabilité
conjointe est :
, alors la fonction de densité de probabilité
conjointe est :
| ρ(δ, Φ) | = ρδ(δ)ρΦ(Φ) | ||
= 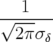 e− e−
 e− e−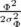
| |||
=  e− e−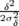 − −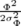
| (4.8) |
La fonction densité de probabilité  dans les nouvelles variables amplitude-phase
dans les nouvelles variables amplitude-phase  se
déduit immédiatement (Eq. 4.4 et 4.8) :
se
déduit immédiatement (Eq. 4.4 et 4.8) :
 | (4.9) |
où  est le jacobien de la transformation continue de coordonnées 4.4 :
est le jacobien de la transformation continue de coordonnées 4.4 : 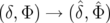 .
.
Le mouvement du centroïde (Eq. 4.7) devient en utilisant l’équation 4.9 :
| < x(n) > | = x0 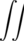  ( (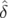 , ,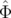 ){cos(2πνxn + φx) cos(Δφx( ){cos(2πνxn + φx) cos(Δφx(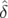 , ,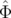 ,n)) ,n)) | ||
− sin(2πνxn + φx) sin(Δφx(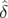 , , ,n))}d ,n))}d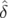 d d | (4.10) | ||
| la sommation sur les sinus s’annule, car la fonction intégrée est impaire, d’où : | |||
| < x(n) > | = x0 cos(2πνxn + φx) ∫
0+∞ d d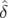 | (4.11) | |
| en utilisant la fonction de Bessel J0 (formule 9.1.18 in Abramowitz et Stegun, 1972) : | |||
| J0 (z) | =  ∫
0π cos(z cos(θ)) dθ ∫
0π cos(z cos(θ)) dθ | (4.12) | |
| < x(n) > | = x0 cos(2πνxn + φx) ∫
0+∞ e− e− 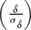 2
J0 2
J0 d d | (4.13) | |
| et finalement avec la formule 11.4.29 (in Abramowitz et Stegun, 1972) : | |||
∫
0+∞e−μ2t2
tη+1J
η(λt) dt =  e− e−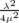
| (4.14) | ||
 | (4.15) |
Le centroïde du faisceau effectue des oscillations bétatrons modulées par le facteur chromatique
 . Ce dernier est une fonction
. Ce dernier est une fonction  -périodique dont les extrema
sont
-périodique dont les extrema
sont 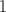 et
et 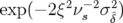 . Au premier ordre, la fréquence d’oscillation du centroïde n’est pas
modifiée, car la distribution des phases bétatrons est symétrique par rapport à la phase
synchrone.
. Au premier ordre, la fréquence d’oscillation du centroïde n’est pas
modifiée, car la distribution des phases bétatrons est symétrique par rapport à la phase
synchrone.
Supposons que la fréquence transverse dépende quadratiquement de l’amplitude d’oscillation 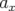 ,
i.e. :
,
i.e. :
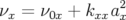 | (4.16) |
Alors le déphase au n-ième tour s’écrit :
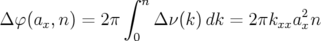 | (4.17) |
L’oscillation bétatron de la particule devient (cf. formule 1.60 p. § avec  ) :
) :
 | (4.18) |
et celle du centroïde de particules distribuées statistiquement selon  :
:
 | (4.19) |
Si 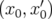 sont les variables de l’espace des phases transverse, alors on sait que l’invariant linéaire
est l’intégrale d’action (cf. définition de l’émittance p. §) :
sont les variables de l’espace des phases transverse, alors on sait que l’invariant linéaire
est l’intégrale d’action (cf. définition de l’émittance p. §) :
![1 2 ′ 2
Jx0 = 2β--[x 0 + (αxx0 + βxx 0) ]
x](these1691x.png) | (4.20) |
avec 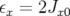 . En supposant des distributions gaussiennes, la fonction densité de probabilité
avant l’impulsion est alors donnée par :
. En supposant des distributions gaussiennes, la fonction densité de probabilité
avant l’impulsion est alors donnée par :
 | (4.21) |
avec  . La distribution dans les variables amplitude-phase
. La distribution dans les variables amplitude-phase 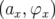 est
alors :
est
alors :
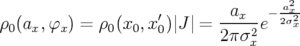 | (4.22) |
avec  et
et
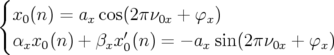 | (4.23) |
La distribution recherchée est celle obtenue immédiatement après que le faisceau a reçu une
impulsion  . On suppose ici que le faisceau est déplacé d’un bloc instantanément au temps
. On suppose ici que le faisceau est déplacé d’un bloc instantanément au temps
 . On déduit alors (cf. Eq. 4.22 et Fig. 4.3) :
. On déduit alors (cf. Eq. 4.22 et Fig. 4.3) :
 | (4.24) |
avec l’amplitude de l’impulsion transverse  .
.
|
|
Le mouvement du centroïde du paquet de particules se réécrit alors (Eq. 4.19 et 4.24) :
| < x(n) > | = ∫
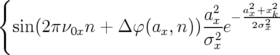 | ||
 dax dax | (4.25) | ||
| l’intégrale sur les cosinus étant nulle, | |||
| < x(n) > | = ∫
 e− e− 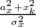 I1
I1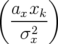 sin(2πν0xn + Δφ(ax,n)) dax sin(2πν0xn + Δφ(ax,n)) dax | (4.26) | |
| avec la fonction de Bessel modifiée I1(x) : | |||
| I1(x) | =  ∫
0π cos(θ)eix cos θ dθ ∫
0π cos(θ)eix cos θ dθ | (4.27) | |
| < x(n) > | = −xkFx sin  | (4.28) | |
| avec | Fx = 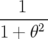 exp exp 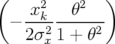 , θ = 4πkxxσx2n , θ = 4πkxxσx2n | ||
 .
.
La décohérence avec l’amplitude d’oscillation introduit le facteur de décohérence 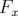 qui
est une gaussienne pour
qui
est une gaussienne pour 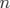 petit et tend asymptotiquement vers une loi en puissance
petit et tend asymptotiquement vers une loi en puissance
 . Le centroïde,
. Le centroïde, 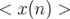 , de phase
, de phase 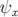 (Eq. 4.28), oscille à la fréquence
instantannée :
(Eq. 4.28), oscille à la fréquence
instantannée :
| νx | =   | (4.29) |
= ν0x + kxx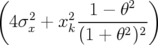 | (4.30) |
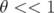 : le faisceau oscille
approximativement à la fréquence
: le faisceau oscille
approximativement à la fréquence 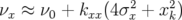 . Le second pour
. Le second pour  , la fréquence
devient
, la fréquence
devient  , ce qui correspond au cas où le faisceau a entièrement « décohéré » (son
amplitude d’oscillation moyenne est nulle).
, ce qui correspond au cas où le faisceau a entièrement « décohéré » (son
amplitude d’oscillation moyenne est nulle).
De manière similaire, on déduit la formule générale pour deux degrés de liberté. On
suppose que le glissement des nombres d’ondes avec l’amplitude est donné en première
approximation par la loi :  et
et  . On déduit alors les
formules :
. On déduit alors les
formules :
| < x(n) > | = −xkFxxFxy sin  | (4.31) |
| < y(n) > | = −ykFyyFyx sin  | (4.32) |
 ,
, 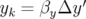 et
et
| θxx = 4πkxxσx2n, θ xy = 4πkxyσy2n | ||
| θyy = 4πkyyσy2n, θ yx = 4πkyxσx2n |
Fxx =  exp exp  , , | Fxy =  exp exp  | ||
Fyy =  exp exp 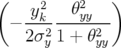 , , | Fyx =  exp exp  |
 :
:
 | (4.33) |
Le phénomène de décohérence complique la dynamique du centroïde observé dont le mouvement peut être décrit par une loi de la forme7 (Eq. 4.15 et 4.32) :
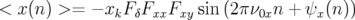 | (4.34) |
avec  .
.
La chromaticité ne modifie pas la fréquence d’oscillation mais introduit un facteur de
modulation périodique de l’enveloppe du faisceau, le facteur chromatique 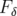 . Par contre, le
glissement des nombres d’ondes introduit non seulement un facteur de décohérence non
périodique par degré de liberté
. Par contre, le
glissement des nombres d’ondes introduit non seulement un facteur de décohérence non
périodique par degré de liberté  et
et  , mais aussi un glissement des nombres
d’ondes. Remarquons que dans le cas où ce dernier terme est important, le signal n’est plus
quasi-périodique.
, mais aussi un glissement des nombres
d’ondes. Remarquons que dans le cas où ce dernier terme est important, le signal n’est plus
quasi-périodique.
Avant le début des mesures, l’orbite fermée (défauts dipolaires) a été corrigée avec le plus grand
soin. Les données tour par tour sont ensuite collectées sur un BPM constitué de quatre électrodes
numérotées de 1 à 4 (cf. schéma 4.4). Les signaux horizontal et vertical sont alors reconstruits
connaissant les gains 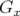 et
et  du BPM :
du BPM :
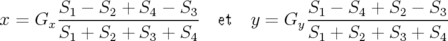 | (4.35) |
avec 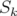 le signal collecté sur la k-ième électrode.
le signal collecté sur la k-ième électrode.
La décohérence est nettement observée (cf. Fig. 4.5) : aux faibles amplitudes, elle a lieu sur environ 600 tours, i.e. qu’au-delà le signal est noyé dans le bruit ; aux grandes, la décohérence est très rapide : 150 tours environ. Pratiquement, les implications sont les suivantes : le signal n’est pas quasi-périodique, il va être difficile d’extraire la fréquence avec une grande précision. Lorsque que le signal utile est contenu uniquement dans les 150 premières données, l’utilisation d’une FFT traditionnelle est presque illusoire et l’Analyse en Fréquence doit être utilisée avec grande précaution.
|
|
La réduction des données peut alors se faire avec plus ou moins de succès de différentes manières :
Aux grandes amplitudes, on observe un début de saturation des BPM ainsi que l’apparition de comportement nonlinéaires du faisceau, ce qui va induire une diminution de la précision pour la détermination des fréquences qui était déjà compliquée par le faible nombre de données contenant du signal.
|
|
L’Analyse en Fréquence a été réalisée pour  conditions initiales. A la lecture de la
carte en fréquence obtenue (cf. Fig. 4.7-a), il est frappant de voir combien les structures
résonantes se lisent clairement. Deux résonances de couplage d’ordre 5 sont nettement
observées :
conditions initiales. A la lecture de la
carte en fréquence obtenue (cf. Fig. 4.7-a), il est frappant de voir combien les structures
résonantes se lisent clairement. Deux résonances de couplage d’ordre 5 sont nettement
observées : 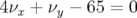 et
et  . Non seulement, leur coefficient
d’excitation est élevé mais de plus, ces résonances sont normalement interdites par la
12-périodicité, et n’étaient donc pas vues aussi nettement sur la carte en fréquence
théorique8.
Elles sont excitées par les gradients résiduels et les erreurs de couplage qui détruisent la symétrie
interne. Une troisième résonance d’ordre 5
. Non seulement, leur coefficient
d’excitation est élevé mais de plus, ces résonances sont normalement interdites par la
12-périodicité, et n’étaient donc pas vues aussi nettement sur la carte en fréquence
théorique8.
Elles sont excitées par les gradients résiduels et les erreurs de couplage qui détruisent la symétrie
interne. Une troisième résonance d’ordre 5 , est plus faiblement excitée. Ceci
prouve que notre modélisation n’est pas encore parfaite en particulier en ce qui concerne les erreurs
aléatoires.
, est plus faiblement excitée. Ceci
prouve que notre modélisation n’est pas encore parfaite en particulier en ce qui concerne les erreurs
aléatoires.
Remarquons que l’espacement régulier des points dans l’espace des fréquences observés à faible amplitude horizontale peut être directement lié à la précision de nos mesures.
De manière à vérifier notre modèle de calibration, nous avons calculé une carte en fréquence en utilisant les défauts de gradients droits et tournés déduits de la matrice-réponse mesurée le même jour — le code DESPOT a été utilisé —. L’accord entre les deux cartes est excellent (cf. Fig. 4.7). Nous pouvons en conclure qu’un modèle utilisant uniquement les forces hexapolaires nominales, les erreurs de couplage et de gradient calibrés à partir de la matrice-réponse expérimentale permet de décrire la dynamique de l’ALS de manière remarquablement précise.
|
|
Dans le futur, nous pourrons réduire le temps d’acquisition d’une carte en fréquence, et utiliser l’Analyse en Fréquence comme outil de diagnostic en ligne de la dynamique du faisceau.
L’Analyse en Fréquence peut être utilisée pour tracer une carte en fréquence de manière
indépendamment de tout modèle. Comme illustration directe, nous avons volontairement modifié le
point de fonctionnement  . Dans ce cas, la carte en fréquence
expérimentale révèle des résonances très fortes,
. Dans ce cas, la carte en fréquence
expérimentale révèle des résonances très fortes,  ,
,  ,
,
 et
et  (cf. Fig. 4.8, voir aussi la carte en couleur B.15). Au
nœud de résonances, la diffusion des particules est très rapide, ce qui correspond expérimentalement
à une réduction de l’efficacité d’injection et de la durée de vie.
(cf. Fig. 4.8, voir aussi la carte en couleur B.15). Au
nœud de résonances, la diffusion des particules est très rapide, ce qui correspond expérimentalement
à une réduction de l’efficacité d’injection et de la durée de vie.
En effet, durant les mesures nous avons enregistré des pertes significatives du faisceau à cette intersection ainsi qu’au-delà, car des particules ayant de plus grandes amplitudes vont traverser cette région à cause de l’amortissement du faisceau. Ce phénomène n’avait pas été observé lors de la première expérience, lorsque le faisceau a été déplacé aux mêmes amplitudes.
Il est clair que lorsque nous observons de tels comportements nous devons soit déterminer une méthode pour réduire l’amplitude des résonances afin d’améliorer la périodicité, soit changer de point de fonctionnement. Il est intéressant de noter que ce point de fonctionnement était le point de fonctionnement choisi à la construction de l’ALS ; il a été utilisé pendant de nombreuses années. Pour ce réglage, l’efficacité d’injection était quelque peu irrégulière. A l’époque, les raisons n’avaient pas été clairement comprises. Le point de fonctionnement avait alors été changé à la valeur actuelle suite à l’application de l’Analyse en Fréquence (Laskar et Robin, 1996).
|
|
Plusieurs cartes en fréquences expérimentales ont été acquises afin de mieux évaluer les effets des wigglers sur la dynamique globale du faisceau. Les résultats n’ont pas encore été complètement exploités. De plus, il n’est pas aisé de modéliser les wigglers de l’ALS et leur influence est très importante sur la dynamique de l’anneau.
Par exemple lorsque le wiggler « W16 » est fermée, il perturbe avant correction fortement
l’optique : il induit un glissement du nombre d’ondes vertical ( ), un fort battement
des fonctions bétatrons (
), un fort battement
des fonctions bétatrons ( ). La 12-périodicité de l’anneau est également altérée. Il
s’ensuit une baisse drastique des performances de l’anneau (durée de vie, taille du faisceau,
émittances). Il est impossible de corriger localement les effets de ce wiggler à l’ALS. Une correction
globale — mais pas totale — est réalisé en utilisant 48 des quadripôles de la machine (Robin,
Safranek, Decking, Nishimura, 1998).
). La 12-périodicité de l’anneau est également altérée. Il
s’ensuit une baisse drastique des performances de l’anneau (durée de vie, taille du faisceau,
émittances). Il est impossible de corriger localement les effets de ce wiggler à l’ALS. Une correction
globale — mais pas totale — est réalisé en utilisant 48 des quadripôles de la machine (Robin,
Safranek, Decking, Nishimura, 1998).
Nous nous contentons ici de présenter une carte en fréquence expérimentale (Fig. 4.9-a) avec
comme point de fonctionnement  . L’accord avec les simulations
numériques (Fig. 4.9-b) est moins probant que précédemment ; notre modèle des wigglers
demande à être amélioré. Les cartes en fréquence (Fig. 4.10) sont tracées en balayant
toute l’ouverture dynamique pour des points de fonctionnement voisins. Ces simulations
prennent en compte le wiggler W16, les défauts quadripolaires droits et tournés déduits des
matrices-réponse mesurées juste avant d’acquérir la carte en fréquence expérimentale
précédente.
. L’accord avec les simulations
numériques (Fig. 4.9-b) est moins probant que précédemment ; notre modèle des wigglers
demande à être amélioré. Les cartes en fréquence (Fig. 4.10) sont tracées en balayant
toute l’ouverture dynamique pour des points de fonctionnement voisins. Ces simulations
prennent en compte le wiggler W16, les défauts quadripolaires droits et tournés déduits des
matrices-réponse mesurées juste avant d’acquérir la carte en fréquence expérimentale
précédente.
|
|
|
|
Même si certaines expériences sur d’autres accélérateurs ont déjà utilisé l’association aimants rapides et de BPM tour par tour pour étudier la dynamique nonlinéaire (Lee, 1992) et si des tentatives pour relier l’Analyse en Fréquence et les mesures de fréquences ont été entreprises (Terebilo et al., 1998 — Bartolini et al., 1999) ; à notre connaissance, les résultats présentés sont les premiers de ce genre.
La réalisation de cartes en fréquence expérimentales à l’ALS montre le réseau complet de résonances d’un système hamiltonien à trois degrés de liberté. La comparaison entre les cartes en fréquence théoriques et mesurées démontre qu’un modèle relativement simple peut être utilisé pour caractériser correctement la dynamique du faisceau, i.e. en prenant en compte les forces nominales des hexapôles et les erreurs de gradients droits et tournés. Cet accord impressionnant nous permet d’utiliser dès maintenant de manière fiable l’Analyse en Fréquence comme outil standard pour faire de la prédiction de l’impact sur dynamique d’une modification de la maille de l’ALS. L’Analyse en Fréquence peut être utilisée pour optimiser nos simulations et pour valider notre modèle de l’anneau. La capacité de pouvoir calculer des cartes en fréquence indépendamment de tout modèle a été démontrée et l’interprétation de la diffusion sur les cartes en fréquence a été validée par les mesures de perte de faisceau sur les structures résonantes.
Toutes les simulations réalisées jusqu’ici ont été faites dans l’hypothèse que la dynamique de
l’anneau de stockage est gouvernée principalement par la dynamique transverse faiblement
perturbée par la dynamique longitudinale — négligée dans nos simulations puisque que le couplage
synchro-bétatron est quasi-nul —. C’est bien ce qui a été observé sur les cartes en fréquence
expérimentales. Au sujet de la diffusion des orbites, le phénomène est plus complexe que nous
l’avons laissé entendre. La dynamique totale de l’accélérateur peut être décrite par un Hamiltonien
à trois degrés de liberté dépendant de la longitude  pris comme variable indépendante. L’espace
des phases est de dimensions
pris comme variable indépendante. L’espace
des phases est de dimensions  , l’application fréquence est alors une application de
, l’application fréquence est alors une application de  dans
dans  :
:

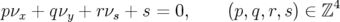 |
Les cartes en fréquence que nous avons tracées dans tout ce manuscrit ne sont qu’une projection
dans le plan 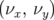 . Ce qui signifie en particulier, que même dans une zone parfaitement
régulière d’une carte en fréquence, il peut y avoir une diffusion due au degré de liberté longitudinal.
Cependant, elle reste généralement très faible vis-à-vis de celles induites par la dynamique
transverse.
. Ce qui signifie en particulier, que même dans une zone parfaitement
régulière d’une carte en fréquence, il peut y avoir une diffusion due au degré de liberté longitudinal.
Cependant, elle reste généralement très faible vis-à-vis de celles induites par la dynamique
transverse.
Au cours de l’été 2001, la maille de l’ALS va connaître sa plus importante modification : trois
des trente-six dipôles de la machine vont être remplacés par des aimants supraconducteurs. La
périodicité de la machine va diminuer pour passer de 12 à 3. Pour une énergie nominale de
1.9 GeV, les fluctuations quantiques des aimants supra-conducteurs augmentent l’émittance
horizontale de 5.5 à 13 nm.rad. Cette dernière peut être réduite en introduisant de la dispersion
dans les sections droites. Le couplage (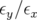 ) est néanmoins inférieur à 1%, et le temps
de vie du faisceau n’est que d’environ deux heures (pour un courant de 1.3 mA par
paquet). Pour retrouver un temps de vie acceptable, l’émittance verticale devra être
augmentée en introduisant une dizaine de nouvelles familles de quadripôles tournés (cf.
simulations de Nishimura et Robin, 1999). Nous comptons utiliser pleinement l’Analyse en
Fréquence pour finir de comprendre l’influence de ses modifications — le but idéal serait
d’arriver à les compenser entièrement — et de continuer d’améliorer les performances de
l’ALS.
) est néanmoins inférieur à 1%, et le temps
de vie du faisceau n’est que d’environ deux heures (pour un courant de 1.3 mA par
paquet). Pour retrouver un temps de vie acceptable, l’émittance verticale devra être
augmentée en introduisant une dizaine de nouvelles familles de quadripôles tournés (cf.
simulations de Nishimura et Robin, 1999). Nous comptons utiliser pleinement l’Analyse en
Fréquence pour finir de comprendre l’influence de ses modifications — le but idéal serait
d’arriver à les compenser entièrement — et de continuer d’améliorer les performances de
l’ALS.