Chapitre 5
Super-ACO
L’étude expérimentale de Super-ACO dans le cadre de ce travail était assez naturelle : après le gel
du projet SOLEIL, l’équipe faisceau de l’Unité de Gestion SOLEIL composée de membres de
l’IN2P3, du CEA et du CNRS a été dissoute. L’équipe de M.P. Level, et en particulier A. Nadji,
m’a tout de suite proposé de poursuivre mon travail au LURE et m’a offert la possibilité de réaliser
de fructueuses et enrichissantes expériences directement sur l’anneau de stockage. Bien que
Super-ACO soit en fonctionnement depuis bientôt quinze ans, les performances atteintes sont encore
mal comprises : durée de vie, efficacité d’injection, limitation de l’acceptance dynamique et en
énergie, résonances.
Un travail important avait déjà été réalisé, mais de nombreuses contraintes extérieures et
utilisateurs ne permettent pas aux physiciens des accélérateurs de caractériser exhaustivement leur
machine comme ils le souhaiteraient.
Différentes études ont été menées durant la dernière année de ma thèse. Tout d’abord une
caractérisation du point de fonctionnement actuel de Super-ACO à travers l’Analyse en Fréquence
(ouverture dynamique, carte en fréquence et résonances cf. chap. 3, p. sqq.). Puis, pour affiner
notre connaissance de la dynamique linéaire, similairement au travail effectué à l’ALS, je désirais
connaître précisément les principaux défauts magnétiques mesurés de l’anneau. Or, nous ne
disposions que de mesures magnétiques réalisées sur banc d’essai à la fin des années
1980. Nous avons donc décidé d’appliquer la méthode développée par J. Safranek : le
programme LOCO que je présenterai succinctement (section 5.1). Enfin, perplexe vis-à-vis des
résultats obtenus sur Super-ACO, j’ai proposé plusieurs expériences visant aux premières
mesures du glissement des nombres d’ondes avec l’amplitude horizontale. Ces derniers
résultats donneront un éclairage nouveau sur la dynamique globale de l’anneau (section 5.2
et section 5.3). Les résultats présentés sont extraits de rapports internes écrits pour
le groupe accélérateur du LURE. Initialement, ces rapports ont été écrits de manière
indépendante sous forme de notes d’expérience. J’espère que le lecteur me pardonnera quelques
redites et un style moins soutenu. Pour faciliter la lecture, les parties techniques non
fondamentales pour la compréhension des résultats sont écrites avec une police plus
petite.
5.1 Acquisition des matrices-réponse
5.1.1 Description du programme LOCO
Dans un anneau de stockage, la périodicité interne permet d’améliorer la dynamique du faisceau en
limitant le nombre de résonances pouvant être excitées ; cependant la présence de défauts
quadripolaires
est une des causes principales de brisure de cette symétrie et entraîne souvent une détérioration de
la durée de vie et du taux d’injection via l’excitation de nonlinéarités. Donc, lorsque l’on désire
optimiser une machine, une connaissance précise des défauts magnétiques est nécessaire pour
établir un modèle aussi réaliste que possible ; alors seulement, les calculs d’ouverture dynamique, de
carte en fréquence prennent tout leur sens.
Le programme LOCO (Linear Optics from Closed Orbits) a été écrit par Safranek (1997) dans cette
optique pour analyser la matrice-réponse du National Synchrotron Light Source de Brookhaven et en
déduire les gradients des quadripôles, les défauts des éléments magnétiques (alignements, rotations des
éléments). Tout le programme repose sur l’analyse de l’orbite fermée en approximation linéaire. Cette
méthode
a déjà eu de nombreuses applications — voir par exemple pour l’Advanced Light Source (Robin et
al., 1996) et pour l’anneau VUV du National Synchrotron Source (Safranek et Kramer, 1997)
—
Dans ce travail, on se propose d’appliquer LOCO à Super-ACO. Dans une première partie, la
méthode de calcul de la matrice-réponse est rappelée. Puis l’utilisation du programme LOCO est
présentée et testée sur un exemple simple. Enfin, l’expérience du 19 juin 2000 est dépouillée : trois
matrices-réponse ont été acquises pour trois configurations distinctes : hexapôles éteints, hexapôles
allumés, hexapôles allumés et onduleurs fermés.
Le principal objectif est d’établir le jeu de défauts des gradients pour chaque cas et de valider la
méthode. En discussion, une application des résultats est proposée pour restaurer la symétrie de
Super-ACO.
5.1.1.1 Perturbation de l’orbite fermée par un kick dipolaire
Soit un dipôle fin de longueur  , situé en
, situé en  , donnant un angle ou impulsion (kick en
anglais)
, donnant un angle ou impulsion (kick en
anglais)  à une particule, avec
à une particule, avec  la rigidité magnétique et
la rigidité magnétique et 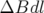 le champ
dipolaire intégré. Si juste avant l’impulsion, l’orbite fermée est
le champ
dipolaire intégré. Si juste avant l’impulsion, l’orbite fermée est  , alors juste après
l’impulsion, elle devient
, alors juste après
l’impulsion, elle devient  . Trouver l’expression de l’orbite fermée
. Trouver l’expression de l’orbite fermée 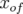 en
en 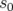 revient à
résoudre la relation de fermeture :
revient à
résoudre la relation de fermeture :
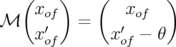 | (5.1) |
où 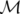 est la matrice de transfert de l’anneau sur un tour. La solution, exprimée en fonction des
paramètres de Twiss
est la matrice de transfert de l’anneau sur un tour. La solution, exprimée en fonction des
paramètres de Twiss 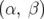 , du nombre d’ondes
, du nombre d’ondes  , est alors :
, est alors :
Pour déduire l’expression de l’orbite fermée résultante en un endroit  quelconque de
l’anneau, il suffit de propager la solution trouvée en
quelconque de
l’anneau, il suffit de propager la solution trouvée en  en utilisant la fonction de Green,
en utilisant la fonction de Green,
 , de l’équation de Hill :
, de l’équation de Hill :
5.1.1.2 Matrice-réponse
Pour un jeu de défauts dipolaires  , en utilisant la linéarité de l’équation de Hill en la
perturbation dipolaire, l’orbite fermée résultante est simplement la superposition des orbites
fermées individuelles créées par une impulsion
, en utilisant la linéarité de l’équation de Hill en la
perturbation dipolaire, l’orbite fermée résultante est simplement la superposition des orbites
fermées individuelles créées par une impulsion  (cf. Eq. 5.2), soit :
(cf. Eq. 5.2), soit :
La matrice 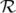 est appelée matrice-réponse linéaire de l’orbite fermée. Elle est constituée de
est appelée matrice-réponse linéaire de l’orbite fermée. Elle est constituée de 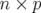 éléments pour une machine comportant
éléments pour une machine comportant  correcteurs dipolaires et
correcteurs dipolaires et 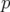 BPM (Beam Position
Monitors : stations de mesure de position).
BPM (Beam Position
Monitors : stations de mesure de position).
En expérience et en simulation avec le programme
MAD
[50], la matrice-réponse est construite en allumant l’un après l’autre les 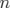 correcteurs et en
enregistrant dans chacun des
correcteurs et en
enregistrant dans chacun des 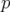 BPM l’orbite fermée générée.
BPM l’orbite fermée générée.
Expérimentalement, deux matrices sont construites : une pour des kicks d’angle  et une
autre pour des kicks d’angle
et une
autre pour des kicks d’angle  . En effet, il subsiste une orbite fermée résiduelle créée par les
nonlinéarités des champs magnétiques. En calculant la différence de ces deux matrices, on élimine
ainsi l’orbite fermée résiduelle et l’on obtient une matrice-réponse équivalente à un kick d’angle
. En effet, il subsiste une orbite fermée résiduelle créée par les
nonlinéarités des champs magnétiques. En calculant la différence de ces deux matrices, on élimine
ainsi l’orbite fermée résiduelle et l’on obtient une matrice-réponse équivalente à un kick d’angle
 .
.
Le choix de la valeur du kick dipolaire est guidé par les deux considérations suivantes : d’une
part, une grande valeur de 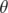 permet d’augmenter le rapport signal sur bruit de la mesure et donc
de réduire la barre d’erreur sur les valeurs de gradients trouvées par rapport au bruit aléatoire des
BPM ; d’autre part, une faible valeur de
permet d’augmenter le rapport signal sur bruit de la mesure et donc
de réduire la barre d’erreur sur les valeurs de gradients trouvées par rapport au bruit aléatoire des
BPM ; d’autre part, une faible valeur de  permet de s’affranchir des nonlinéarités mais aussi de
rester dans une gamme de réponse linéaire de l’électronique. Une valeur intermédiaire doit donc
être choisie : en pratique des kicks de valeur induisant une perturbation de l’orbite fermée de
permet de s’affranchir des nonlinéarités mais aussi de
rester dans une gamme de réponse linéaire de l’électronique. Une valeur intermédiaire doit donc
être choisie : en pratique des kicks de valeur induisant une perturbation de l’orbite fermée de  mm rms (valeur optimale pour le NSLS X-Ray Ring à Brookhaven :
mm rms (valeur optimale pour le NSLS X-Ray Ring à Brookhaven : 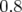 mm rms — Safranek, 1997
—).
mm rms — Safranek, 1997
—).
Le programme LOCO utilise une méthode des moindres carrés pour minimiser le «  » entre
la matrice-réponse modèle,
» entre
la matrice-réponse modèle,  , et la matrice-réponse expérimentale,
, et la matrice-réponse expérimentale, 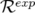 , en ajustant les
gradients quadripolaires :
, en ajustant les
gradients quadripolaires :
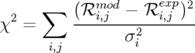 | (5.4) |
où la sommation a lieu sur les BPM  et les correcteurs
et les correcteurs 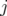 , normalisée par le bruit des BPM
, normalisée par le bruit des BPM  et
en utilisant une méthode de décomposition en valeurs singulières (SVD [96]). Les autres
paramètres pouvant être incorporés dans l’ajustement de la matrice-réponse non couplée sont
les gains des correcteurs (
et
en utilisant une méthode de décomposition en valeurs singulières (SVD [96]). Les autres
paramètres pouvant être incorporés dans l’ajustement de la matrice-réponse non couplée sont
les gains des correcteurs (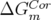 ), les gains des BPM (
), les gains des BPM ( ) et le glissement de
l’énergie (
) et le glissement de
l’énergie (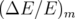 ). Pour la matrice couplée, il faut ajouter la rotation des BPM et des
correcteurs.
). Pour la matrice couplée, il faut ajouter la rotation des BPM et des
correcteurs.
Minimiser le 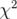 revient à minimiser la norme du vecteur
revient à minimiser la norme du vecteur  dont les composantes sont définies
par :
dont les composantes sont définies
par :
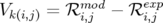 | (5.5) |
où l’indice 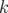 varie de
varie de  à
à 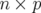 . Alors en approximation linéaire, on
obtient :
. Alors en approximation linéaire, on
obtient :
La valeur escomptée du  est le nombre de degrés de liberté, soit
est le nombre de degrés de liberté, soit  avec un écart
type
avec un écart
type  avec
avec 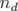 le nombre de données (taille du vecteur
le nombre de données (taille du vecteur  ) et
) et  le
nombre de paramètres ajustés (cf. Modeling of Data, chap. 15 in Numerical Recipes,
1992).
le
nombre de paramètres ajustés (cf. Modeling of Data, chap. 15 in Numerical Recipes,
1992).
5.1.2 Application à Super-ACO
La machine Super-ACO dispose de 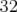 correcteurs,
correcteurs, 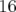 verticaux (dans les
quadripôles défocalisant, i.e. les familles Q1 et Q4) et
verticaux (dans les
quadripôles défocalisant, i.e. les familles Q1 et Q4) et 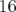 horizontaux (dans les
quadripôles focalisant, i.e. les familles Q2 et Q3). De plus, il existe
horizontaux (dans les
quadripôles focalisant, i.e. les familles Q2 et Q3). De plus, il existe  autres
correcteurs horizontaux, chacun situé dans un dipôle (non utilisés dans la présente
étude ).
autres
correcteurs horizontaux, chacun situé dans un dipôle (non utilisés dans la présente
étude ).
Les  BPM composés de quatre électrodes se trouvent dans chacun des doublets de
quadripôles (cf. maille Fig. 5.1).
BPM composés de quatre électrodes se trouvent dans chacun des doublets de
quadripôles (cf. maille Fig. 5.1).
Je rappelle qu’une des spécificités de Super-ACO tient dans ses quadripôles combinés : dans
chaque quadripôle (Q), il y a aussi un hexapôle (H) possédant un terme décapolaire important
simulé par une lentille décapolaire (LD) et un correcteur dipolaire (cf. Fig. 5.2). Nous verrons plus
tard (cf. section 5.1.6) que le fait d’avoir plusieurs composantes multipolaires et un correcteur dans
un même élément physique peut compliquer la physique de l’anneau et l’interprétation des
données.
5.1.2.1 Procédure adoptée
La version actuelle de LOCO ne peut pas être utilisée de manière automatique : les itérations sont faites
manuellement jusqu’à ce que la convergence soit atteinte. Généralement, trois à quatre itérations suffisent. La
procédure d’utilisation du programme LOCO résulte d’une discussion avec J. Safranek (SLAC), D. Robin (ALS) et
C. Steier (ALS).
Hexapôles éteints
- Ajuster les gains des correcteurs.
- Ajouter les gradients quadripolaires.
- Ajouter les gains des BPM.
- Ajouter tout le reste.
Hexapôles allumés
- Partir des gradients trouvés précédemment.
- Ajuster les gains des correcteurs.
- Ajouter les gradients de hexapôles.
- Ajouter les gains des BPM.
- Ajouter tout le reste.
5.1.3 Etude préliminaire
Pour le début de l’étude, on ne considère que les 32 correcteurs situés dans les quadripôles. Pour s’affranchir des
nonlinéarités, les hexapôles et les lentilles décapolaires sont éteints. Dans un premier temps, on a voulu s’assurer que
si l’on donne à LOCO comme matrice expérimentale la matrice théorique alors LOCO donne l’ajustement
parfait.
5.1.3.1 Conditions du test
L’ajustement est réalisé uniquement sur les gradients des quatre familles de quadripôles  ,
, 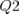 ,
,  ,
, 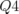 . La
fonction dispersion est supposée nulle tout autour de la machine pour s’affranchir du facteur d’Amman (cf.
infra).
. La
fonction dispersion est supposée nulle tout autour de la machine pour s’affranchir du facteur d’Amman (cf.
infra).
5.1.3.2 Résultats
Au bout de deux itérations, l’algorithme converge. Les petits écarts observés s’expliquent par le nombre de chiffres
significatifs entrés dans la matrice-réponse expérimentale simulée en tant que modèle. A la lecture du tableau 5.1, les
valeurs rms résiduelles sont négligeables compte tenu de la précision (arrondis à deux chiffres significatifs). 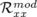 et
et
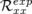 (resp.
(resp.  et
et  ) sont les valeurs rms en millimètres des matrices-réponse théorique
et expérimentale horizontales (resp. verticales).
) sont les valeurs rms en millimètres des matrices-réponse théorique
et expérimentale horizontales (resp. verticales). 
 et
et 
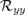 donnent l’écart rms entre ces
matrices.
donnent l’écart rms entre ces
matrices.
En pratique, l’orbite fermée est mesurée sur Super-ACO avec seulement deux chiffres significatifs. Pour avoir une
bonne convergence numérique, les données sont complétées par des zéros pour ces tests. En prenant huit chiffres
significatifs, l’ajustement est parfait, i.e. avec erreur relative de l’ordre de la précision machine (cf.
infra).
5.1.3.3 Test complet du modèle
Pour vérifier le bon fonctionnement du programme LOCO, on simule des défauts sur les gradients des quadripôles en
conservant la symétrie quatre de l’anneau.
Pour commencer, on dérègle le gradient de  de
de 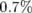 : on observe un glissement des nombres d’ondes :
: on observe un glissement des nombres d’ondes :
 et
et  .
.
Au bout de deux itérations, LOCO retrouve exactement les bonnes valeurs des gradients (comparer les valeurs
attendues et finales du tableau 5.2. Les calculs sont faits en simple précision).
Puis, on dérègle de nouveau le gradient de la première famille 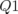 de
de  mais uniquement sur le quadripôle
mais uniquement sur le quadripôle
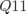 on observe un glissement des nombres d’ondes
on observe un glissement des nombres d’ondes  et
et  . Encore une fois, le programme
LOCO converge en trois itérations vers les valeurs escomptées avec les bons nombres d’ondes (cf. tableau
5.3).
. Encore une fois, le programme
LOCO converge en trois itérations vers les valeurs escomptées avec les bons nombres d’ondes (cf. tableau
5.3).
Objectifs
Le but de l’expérience du 19 juin 2000 était d’acquérir les matrices-réponse expérimentales de
Super-ACO pour le point de fonctionnement nominal afin d’en déduire par ajustement les fonctions
bétatrons de la machine puis les distributions correspondantes de gradients. Trois matrices ont
été acquises, une avec les hexapôles éteints et onduleurs ouverts (section 5.1.5), puis
avec les hexapôles allumés (section 5.1.6) et enfin une dernière en fermant les onduleurs
(section 5.1.7). Dans chacun des cas, le minimum de couplage a été fait mais la chromaticité n’a
pas été mesurée. En utilisant le programme LOCO (Safranek, 1997), on a cherché à
établir le modèle théorique le plus proche possible de la machine réelle via l’optique
linéaire.
5.1.4 Etapes préliminaires à l’analyse des matrices-réponse
Pour utiliser le programme LOCO, il est nécessaire de faire deux mesures supplémentaires :
- une mesure du bruit rms des 16 BPM.
- une mesure de la fonction dispersion dans chaque BPM.
5.1.4.1 Bruit moyen des BPM
Deux jeux de données ont été mesurés :
- 1 000 orbites au début de l’expérience, avec les hexapôles éteints et les onduleurs ouverts.
- 100 orbites en fin d’expériences, hexapôles allumés et les onduleurs fermés.
Les figures 5.3 donnent les résultats moyennés pour chaque BPM  ainsi que les valeurs de bruit
rms,
ainsi que les valeurs de bruit
rms, 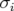 , pour les deux cas considérés. De manière générale, les valeurs de bruits sont plus élevées
en début qu’en fin d’expérience (Tab. 5.4). Le bruit des BPM a également été mesuré le mercredi
20 septembre et mercredi 4 novembre 2000 ; les valeurs rms de bruit dans les deux plans valent
, pour les deux cas considérés. De manière générale, les valeurs de bruits sont plus élevées
en début qu’en fin d’expérience (Tab. 5.4). Le bruit des BPM a également été mesuré le mercredi
20 septembre et mercredi 4 novembre 2000 ; les valeurs rms de bruit dans les deux plans valent
 ,
ce qui correspond à la précision des BPM. Ces valeurs de bruit donnent la limite de convergence
qu’on peut espérer atteindre avec l’algorithme LOCO.
,
ce qui correspond à la précision des BPM. Ces valeurs de bruit donnent la limite de convergence
qu’on peut espérer atteindre avec l’algorithme LOCO.
5.1.4.2 Mesure de la fonction dispersion dans les BPM
La fonction dispersion, 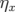 , dans les BPM est calculée avec la formule usuelle (Rice in Chao et
Tigner, 1998) :
, dans les BPM est calculée avec la formule usuelle (Rice in Chao et
Tigner, 1998) :
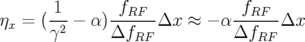 | (5.7) |
avec  , le facteur d’allongement du premier ordre (momentum compaction) et
, le facteur d’allongement du premier ordre (momentum compaction) et 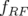 , la
fréquence RF de l’anneau. Pour cela, on réalise deux mesures d’orbite fermée (
, la
fréquence RF de l’anneau. Pour cela, on réalise deux mesures d’orbite fermée ( ), pour deux
fréquences RF distinctes (
), pour deux
fréquences RF distinctes ( ) juste avant l’acquisition de chacune des matrices-réponse (cf.
paramètres Tab. 5.5). L’erreur relative sur la valeur des dispersions est donnée par la formule :
) juste avant l’acquisition de chacune des matrices-réponse (cf.
paramètres Tab. 5.5). L’erreur relative sur la valeur des dispersions est donnée par la formule :
soit en moyenne 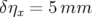 .
.
5.1.5 Matrice-réponse hexapôles éteints et onduleurs ouverts
5.1.5.1 Introduction
On dispose de  BPM,
BPM, 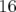 correcteurs horizontaux et 16 correcteurs verticaux, donc la
matrice-réponse non couplée a
correcteurs horizontaux et 16 correcteurs verticaux, donc la
matrice-réponse non couplée a 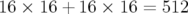 éléments.
éléments.
Pour générer les matrices-réponse, on allume successivement les correcteurs avec un courant de  , soit
approximativement
, soit
approximativement 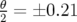 mrad pour un correcteur horizontal et
mrad pour un correcteur horizontal et  mrad pour un correcteur
vertical,
et on mesure dans chaque BPM le déplacement de l’orbite fermée.
mrad pour un correcteur
vertical,
et on mesure dans chaque BPM le déplacement de l’orbite fermée.
L’ajustement entre matrices expérimentale et modèle est réalisé en faisant varier les forces
quadripolaires soit en familles (4), soit individuellement (32), les gains des correcteurs
horizontaux (16) et verticaux (16), les gains des BPM horizontaux (16) et verticaux (16). Pour
finir, dans les sections dispersives, le déplacement supplémentaire de l’orbite associé au
glissement en énergie est pris en compte (parfois appelé facteur d’Amman [Amman,
1971]),
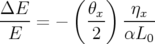 | (5.9) |
avec  le facteur d’allongement du premier ordre et
le facteur d’allongement du premier ordre et  la circonférence de la machine.
la circonférence de la machine.
En effet, la déviation 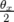 produite par le correcteur dipolaire engendre — si la fonction
dispersion
produite par le correcteur dipolaire engendre — si la fonction
dispersion 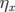 est non nulle — une modification de la longueur
est non nulle — une modification de la longueur 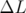 de l’orbite de la
particule :
de l’orbite de la
particule :
 | (5.10) |
allongement équivalent à une modification de l’énergie de la particule :
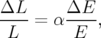 | (5.11) |
ce qui ajoute 16 nouveaux paramètres.
Au total, l’ajustement est réalisé sur 84 (ou 112) paramètres.
Cependant, on ne peut pas faire varier de manière indépendante l’ensemble des gains des BPM
et des correcteurs sous peine de dégénérescence. En effet, si tous les gains des BPM sont augmentés
d’un même facteur alors que ceux des correcteurs sont diminués proportionnellement alors la
matrice-réponse reste inchangée : la SVD donne deux valeurs propres nulles. Pour lever cette
dégénérescence, il suffit de fixer par exemple le gain d’un correcteur horizontal et d’un correcteur
vertical.
5.1.5.2 Conditions expérimentales
Pour l’optique de Super-ACO utilisée, le courant stocké était de  mA dans 24 paquets, en
faisceau « plat »
mA dans 24 paquets, en
faisceau « plat »  , ceci avec les quatre familles d’hexapôles éteintes.
Cette possibilité d’éteindre les hexapôles avec un faisceau circulant dans l’anneau est un
avantage qui permettra de déterminer les défauts de gradients indépendamment de ceux
induits par les hexapôles lorsqu’il existe une orbite résiduelle
, ceci avec les quatre familles d’hexapôles éteintes.
Cette possibilité d’éteindre les hexapôles avec un faisceau circulant dans l’anneau est un
avantage qui permettra de déterminer les défauts de gradients indépendamment de ceux
induits par les hexapôles lorsqu’il existe une orbite résiduelle 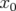 en leur centre (cf.
section 5.1.6).
en leur centre (cf.
section 5.1.6).
|
| | Famille | I(A) |
|
| | Q1 | 222.84 |
| Q2 | 402.50 |
| Q3 | 379.78 |
| Q4 | 216.24 |
|
| | |
| TAB. 5.6: | Courants mesurés dans les alimentations des quatre familles de quadripôles de
Super-ACO — hexapôles éteints, onduleurs ouverts — |
|
Le modèle utilisé est déduit des mesures de courant dans les
quadripôles :
c’est notre modèle de référence de Super-ACO (cf. Tab 5.6). Le point de fonctionnement
théorique devient alors  . Notons que par rapport au point de
fonctionnement nominal, le courant dans
. Notons que par rapport au point de
fonctionnement nominal, le courant dans  ayant changé, les valeurs de la fonction dispersion
théorique sont également légèrement modifiées. Les nombres d’ondes mesurés valent :
ayant changé, les valeurs de la fonction dispersion
théorique sont également légèrement modifiées. Les nombres d’ondes mesurés valent :
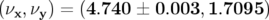 . L’incertitude sur
. L’incertitude sur  provient de la faible valeur du courant
provient de la faible valeur du courant
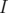 (à l’oscilloscope au lieu d’un pic unique, on en observe plusieurs).
(à l’oscilloscope au lieu d’un pic unique, on en observe plusieurs).
5.1.5.3 Dispersion mesurée dans les BPM
Les résultats sont résumés par la figure 5.4 et le tableau 5.7.
-
Régions non dispersives
- valeur prédite :
 mm ; l’écart modèle/expérience est
grand, en moyenne de 130%.
mm ; l’écart modèle/expérience est
grand, en moyenne de 130%.
-
Régions dispersives
- valeur prédite :
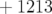 mm ; l’écart modèle/expérience est en
moyenne de 5%.
mm ; l’écart modèle/expérience est en
moyenne de 5%.
|
|
|
| | BPM1 | -64 | BPM09 | -108 |
| BPM2 | 1271 | BPM10 | 1319 |
| BPM3 | 1267 | BPM11 | 1259 |
| BPM4 | -84 | BPM12 | -96 |
| BPM5 | -100 | BPM13 | -64 |
| BPM6 | 1271 | BPM14 | 1259 |
| BPM7 | 1295 | BPM15 | 1247 |
| BPM8 | -112 | BPM16 | -64 |
|
|
|
| | |
| TAB. 5.7: | Dispersion horizontale (mm) mesurée dans les BPM de Super-ACO (précision à
 mm) — hexapôles éteints et onduleurs ouverts — Les écarts relatifs sont plus importants
dans les régions non dispersives (BPM 1, 4, 5, 8, 9, 12, 13 et 16). mm) — hexapôles éteints et onduleurs ouverts — Les écarts relatifs sont plus importants
dans les régions non dispersives (BPM 1, 4, 5, 8, 9, 12, 13 et 16). |
|
La principale raison de ces écarts est la création d’orbite fermée par les défauts de champs
quadripolaires 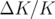 (cf. sous-section 5.1.5.4) suivant la loi (Nadji, 1992).
(cf. sous-section 5.1.5.4) suivant la loi (Nadji, 1992).
En utilisant les résultats de la section suivante, la formule 5.12 donne comme écart moyen sur la
dispersion  mm rms alors que la valeur issue des mesures expérimentales est presque
trois fois plus grande
mm rms alors que la valeur issue des mesures expérimentales est presque
trois fois plus grande 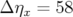 mm rms.
mm rms.
5.1.5.4 Résultats obtenus avec LOCO
Ajustement sur quatre familles :
Avant l’ajustement, le désaccord entre les orbites mesurées et théoriques est supérieur en valeurs
rms à 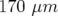 horizontalement (H) et à
horizontalement (H) et à 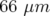 verticalement (V).
verticalement (V).
Après un ajustement sur les quatre familles de quadripôle l’accord est de  (réduction
d’un facteur 5) et
(réduction
d’un facteur 5) et 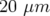 (réduction d’un facteur 3) respectivement dans les plans horizontal et
vertical avec un
(réduction d’un facteur 3) respectivement dans les plans horizontal et
vertical avec un  de 2 080. En suivant les résultats énoncés précédemment, la valeur escomptée
du
de 2 080. En suivant les résultats énoncés précédemment, la valeur escomptée
du 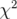 devrait être idéalement au mieux
devrait être idéalement au mieux 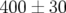 , sachant qu’il y a (
, sachant qu’il y a ( ) points de donnée
et (
) points de donnée
et ( ) paramètres indépendants ajustés. Le point de fonctionnement devient alors
) paramètres indépendants ajustés. Le point de fonctionnement devient alors
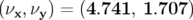 soit
soit  , ce qui est en excellent accord avec
la mesure expérimentale des nombres d’ondes. Les gradients des familles de quadripôles ont varié
de moins de
, ce qui est en excellent accord avec
la mesure expérimentale des nombres d’ondes. Les gradients des familles de quadripôles ont varié
de moins de 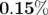 (cf. Tab. 5.8, Fig. 5.5). Il faut remarquer que les écarts relatifs
obtenus pour les gradients sont tous négatifs : ceci ne peut pas être dû à un phénomène
aléatoire.
(cf. Tab. 5.8, Fig. 5.5). Il faut remarquer que les écarts relatifs
obtenus pour les gradients sont tous négatifs : ceci ne peut pas être dû à un phénomène
aléatoire.
|
|
|
| | Famille | Avant | Après |
|
|
|
| | Q1 | -1.46723 | -1.46655 |
| Q2 | 2.62043 | 2.61800 |
| Q3 | 2.47834 | 2.47498 |
| Q4 | -1.42383 | -1.42188 |
|
|
|
| | |
| TAB. 5.8: | Valeurs des gradients
quadripolaires (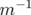 ) en symétrie 4 avant
et après l’ajustement de LOCO. Données
utilisées pour ajuster le modèle linéaire de
Super-ACO. ) en symétrie 4 avant
et après l’ajustement de LOCO. Données
utilisées pour ajuster le modèle linéaire de
Super-ACO. |
|
|
Les nouvelles fonctions  sont tracées sur la figure 5.6 ; le battement (Fig. 5.7) de la fonction
sont tracées sur la figure 5.6 ; le battement (Fig. 5.7) de la fonction
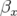 est de
est de  autour de
autour de 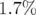 (traduit le glissement
(traduit le glissement  ) et celui de
) et celui de 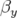 est de
est de
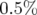 autour de
autour de  (
(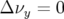 ).
).
Les bruits et gains des BPM ainsi que ceux des correcteurs sont donnés par la figure 5.8. Les
valeurs sont raisonnables ; en moyenne, on retrouve la bonne valeur de kick dipolaire vertical
 . Par contre dans le plan horizontal, la valeur attendue
. Par contre dans le plan horizontal, la valeur attendue 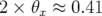 , n’est pas
atteinte dans les régions dispersives. Cet écart est à corréler avec l’écart en dispersion donné par
LOCO (cf. Fig. 5.4).
, n’est pas
atteinte dans les régions dispersives. Cet écart est à corréler avec l’écart en dispersion donné par
LOCO (cf. Fig. 5.4).
Ajustement sur les quadripôles individuels :
Lorsque l’ajustement est réalisé sur les 32 gradients des quadripôles, la symétrie 4 de l’anneau
est brisée. La convergence semble meilleure : 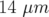 et
et 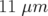 , horizontalement et verticalement
avec comme nombres d’ondes
, horizontalement et verticalement
avec comme nombres d’ondes 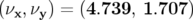 et un
et un  de
de 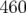 . Les gradients des
quadripôles ont varié de façon plus significative jusqu’à
. Les gradients des
quadripôles ont varié de façon plus significative jusqu’à  (Fig. 5.9). Cependant, cette
variation ne semble pas aléatoire comme l’on s’y attendrait ; bien au contraire, il semble que la
variation sur un quadripôle est rattrapée immédiatement sur le quadripôle suivant. Néanmoins, les
variations en moyenne pour chaque famille correspondent à celles trouvées en symétrie 4.
(Fig. 5.9). Cependant, cette
variation ne semble pas aléatoire comme l’on s’y attendrait ; bien au contraire, il semble que la
variation sur un quadripôle est rattrapée immédiatement sur le quadripôle suivant. Néanmoins, les
variations en moyenne pour chaque famille correspondent à celles trouvées en symétrie 4.
Ces résultats sont assez surprenants. En effet, briser la symétrie 4 de l’anneau devrait
simplement se traduire par une distribution aléatoire des gradients quadripolaires autour
des valeurs trouvées précédemment pour chaque famille. En aucun cas, la justification
de variation de l’ordre du pourcentage ne semble plausible, ce qui est bien au-delà des
valeurs provenant des mesures magnétiques (Barthès et al., 1990, voir Fig. 3.22, p. ). De
plus, une aussi faible valeur du 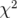 suggère, ou bien que la machine est parfaitement
connue, ou bien que le nombre de paramètres ajustés est trop important. La dernière
hypothèse semble la plus raisonnable : nous essayons d’ajuster 32 valeurs de gradients en
utilisant les mesures de 16 BPM à quatre électrodes. Les autres paramètres, les gains des
correcteurs et des BPM et les facteurs d’Amman, peuvent être vus comme de poids secondaire
dans l’ajustement. Le même type de problème est par exemple rencontré à l’ALS où il y
a 104 gradients quadripolaires à ajuster sur 96 BPM (communication personnelle, C.
Steier).
suggère, ou bien que la machine est parfaitement
connue, ou bien que le nombre de paramètres ajustés est trop important. La dernière
hypothèse semble la plus raisonnable : nous essayons d’ajuster 32 valeurs de gradients en
utilisant les mesures de 16 BPM à quatre électrodes. Les autres paramètres, les gains des
correcteurs et des BPM et les facteurs d’Amman, peuvent être vus comme de poids secondaire
dans l’ajustement. Le même type de problème est par exemple rencontré à l’ALS où il y
a 104 gradients quadripolaires à ajuster sur 96 BPM (communication personnelle, C.
Steier).
Nous voudrions connaître, parmi ces 104 paramètres, combien ont une influence réelle
sur l’ajustement. La réponse à cette question est fournie par l’analyse du spectre des
valeurs propres résultant de la décomposition en valeurs singulières. Sur la figure 5.10, les
valeurs propres (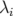 ) sont rangées par ordre décroissant de l’amplitude. On observe une
décroissance rapide des amplitudes avec deux seuils : le premier en
) sont rangées par ordre décroissant de l’amplitude. On observe une
décroissance rapide des amplitudes avec deux seuils : le premier en  , le second en
, le second en 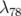 .
.
Ces résultats suggèrent de réaliser l’ajustement en rejetant tous les paramètres conduisant à des
valeurs propres inférieures au seuil 1 ou 2. Il s’avère que ne rejeter que les valeurs propres plus petites que le
seuil 2 n’améliore pas les résultats précédents. Comme attendu à la lecture du spectre, seul le seuil 1 est
significatif :
la convergence est maintenant de  (H) et
(H) et 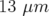 (V) avec comme nouveaux nombres
d’ondes
(V) avec comme nouveaux nombres
d’ondes 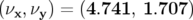 et un
et un 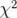 plus élevé de 1 050. La variation des gradients
individuels est aléatoire et avec des amplitudes très voisines de celles obtenues pour les familles de
quadripôles (Fig. 5.11).
plus élevé de 1 050. La variation des gradients
individuels est aléatoire et avec des amplitudes très voisines de celles obtenues pour les familles de
quadripôles (Fig. 5.11).
La convergence est acceptable si l’on considère la valeur moyenne du bruit des BPM, sachant
que de toute manière les mesures ne sont faites avec seulement deux chiffres significatifs, i.e. une
bien faible résolution inhérente à Super-ACO.
A titre indicatif, la figure 5.12 illustre les variations relatives des gradients par rapport aux
valeurs déduites de l’ajustement en familles.
Les nouvelles fonctions  sont tracées sur la figure 5.13. et leurs battements sur la figure 5.14.
Les battements,
sont tracées sur la figure 5.13. et leurs battements sur la figure 5.14.
Les battements, 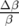 , sont plus importants horizontalement (
, sont plus importants horizontalement (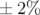 autour de
autour de 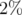 ) que
verticalement
) que
verticalement  . Ils s’expriment en première approximation suivant la formule classique
(Rice et Cornell in Chao et Tigner, 1998) :
. Ils s’expriment en première approximation suivant la formule classique
(Rice et Cornell in Chao et Tigner, 1998) :
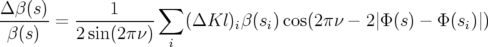 | (5.13) |
où 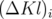 est le gradient intégré du i-ème quadripôle,
est le gradient intégré du i-ème quadripôle,  son avance de phase.
son avance de phase.
Soit avec une formule statistique (Nadji, 1992) :
Soit en prenant les défauts de gradients donnés par LOCO :  , ce qui est en accord
avec la figure 5.14.
, ce qui est en accord
avec la figure 5.14.
On remarque que le battement des fonctions d’ondes est maximum pour un déphasage
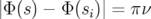 soit pour un défaut dans un quadripôle situé de manière diamétralement
opposée à la position
soit pour un défaut dans un quadripôle situé de manière diamétralement
opposée à la position  du BPM où il est observé.
du BPM où il est observé.
Enfin, LOCO réalisant un ajustement sur le glissement en énergie induit dans les régions
dispersives, on peut en déduire les valeurs des dispersions dans les correcteurs, celles dans les BPM
ont déjà été mesurées (cf. Eq. 5.9). L’ensemble des résultats en comparaison avec les dispersions
déduites de l’ajustement est illustré par la figure 5.15 : l’accord est correct dans les BPM compte
tenu des erreurs de mesure. Cependant, il faut noter des écarts dans les correcteurs entre la
dispersion déduite du facteur d’Amman et celle donnée par le modèle ajusté. De plus, la
dépendance en énergie de la matrice-réponse est traitée trop simplement dans le code LOCO
(communication personnelle, H. Zyngier).
La figure 5.16 donne les nouveaux gains des BPM ainsi que le niveau de bruit de chaque BPM et
correcteur et également la valeur ajustée du kick. On remarquera qu’à la convergence, le bruit rms
du BPM  rapporté au bruit total rms de tous les BPM n’est pas voisin de l’unité comme il
devrait l’être théoriquement pour une convergence atteignant le niveau de bruit des
BPM.
rapporté au bruit total rms de tous les BPM n’est pas voisin de l’unité comme il
devrait l’être théoriquement pour une convergence atteignant le niveau de bruit des
BPM.
En conclusion, l’algorithme LOCO ajuste correctement les fonctions 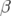 , les nombres d’ondes.
Les défauts de gradients trouvés sont relativement faibles, ce qui suggère un assez bon accord entre
la théorie et l’expérience.
, les nombres d’ondes.
Les défauts de gradients trouvés sont relativement faibles, ce qui suggère un assez bon accord entre
la théorie et l’expérience.
5.1.6 Matrice-réponse hexapôles allumés et onduleurs ouverts
5.1.6.1 Influence des hexapôles
Dans cette partie de l’expérience, une matrice-réponse de Super-ACO a été acquise en allumant les
hexapôles — les onduleurs sont toujours ouverts — Les hexapôles peuvent générer une composante
quadripolaire s’il existe une orbite fermée non nulle comme nous allons le voir. Le potentiel vecteur
d’un hexapôle droit a pour expression :
 | (5.15) |
où 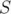 est la force intégrée de l’hexapôle.
est la force intégrée de l’hexapôle.
Si l’orbite fermée n’est plus la trajectoire 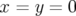 dans l’hexapôle mais
dans l’hexapôle mais  , alors
une composante quadripolaire (et dipolaire) apparaît dans l’expression générale du potentiel
vecteur :
, alors
une composante quadripolaire (et dipolaire) apparaît dans l’expression générale du potentiel
vecteur :
La composante quadripolaire induite est donc :
 | (5.17) |
où  est le champ intégré d’un quadripôle droit et
est le champ intégré d’un quadripôle droit et  celui d’un quadripôle
tourné (à prendre en compte si l’on considère le couplage).
celui d’un quadripôle
tourné (à prendre en compte si l’on considère le couplage).
En partant des valeurs des gradients trouvés précédemment, hexapôles éteints, on peut
maintenant déduire des nouvelles valeurs de gradients, la valeur des champs quadripolaires induits
par chaque hexapôle. De plus, connaissant 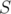 et
et 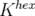 , on peut également déterminer une mesure
de l’orbite fermée,
, on peut également déterminer une mesure
de l’orbite fermée, 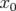 , dans les hexapôles.
, dans les hexapôles.
5.1.6.2 Conditions expérimentales
Un courant  mA a été injecté dans 24 paquets avec un faisceau plat
mA a été injecté dans 24 paquets avec un faisceau plat 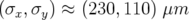 .
Comme les courants alimentant les quadripôles ont changé (cf. Tab. 5.9), il sera plus délicat d’isoler
exactement la contribution quadripolaire induite par les hexapôles seuls et d’appliquer la procédure
précédemment exposée ; le point de fonctionnement déduit des nouvelles valeurs de courant dans les
quadripôles est maintenant
.
Comme les courants alimentant les quadripôles ont changé (cf. Tab. 5.9), il sera plus délicat d’isoler
exactement la contribution quadripolaire induite par les hexapôles seuls et d’appliquer la procédure
précédemment exposée ; le point de fonctionnement déduit des nouvelles valeurs de courant dans les
quadripôles est maintenant 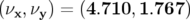 , ce qui est très loin du point de fonctionnement
précédent. Les nombres d’ondes mesurés
sont
, ce qui est très loin du point de fonctionnement
précédent. Les nombres d’ondes mesurés
sont 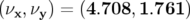 .
.
|
|
|
| | Famille | I(A) | Famille | I(A) |
|
|
|
| | Q1 | 225.37 | H1 | 54.35 |
| Q2 | 401.80 | H2 | 100.31 |
| Q3 | 379.78 | H3 | 198.58 |
| Q4 | 216.24 | H4 | 193.93 |
|
|
|
| | |
| TAB. 5.9: | Courants mesurés pour les quadripôles et hexapôles — onduleurs ouverts —
Valeurs utilisées pour ajuster le modèle de Super-ACO à l’expérience. |
|
A cela, il faut ajouter une question : pour les forces hexapolaires, doit-on prendre les valeurs
déduites du courant les alimentant ou bien celles permettant d’obtenir les bonnes valeurs de
chromaticités — non mesurées lors de l’expérience — ? En effet, rappelons que la chromaticité est
créée :
- naturellement par les quadripôles :
 (cf. chap. 1, p. ).
(cf. chap. 1, p. ).
- par les coins des dipôles
Estimation de la chromaticité naturelle pour ces deux effets :
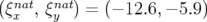
- par les hexapôles :
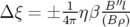 (Edwards et Syphers in Tigner et Chao)
(Edwards et Syphers in Tigner et Chao)
- par les correcteurs dipolaires dans les sections dispersives, car ils possèdent une
composante hexapolaire non négligeable. Il s’agit donc principalement des correcteurs
de la famille CQ3. En partant d’une maille parfaite, on peut estimer cette contribution
à la chromaticité :
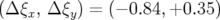
A titre de comparaison, les chromaticités non réduites produites sans prendre en compte les défauts ou les correcteurs
sont 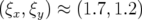 alors que si l’on ne considère que les courants expérimentaux elles valent
alors que si l’on ne considère que les courants expérimentaux elles valent
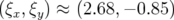 .
De nouvelles mesures de chromaticités ont été réalisées le 30 octobre 2000 pour les mêmes courants
hexapolaires (mais un jeu de correcteurs différent) : hexapôles éteints, on a mesuré seulement
.
De nouvelles mesures de chromaticités ont été réalisées le 30 octobre 2000 pour les mêmes courants
hexapolaires (mais un jeu de correcteurs différent) : hexapôles éteints, on a mesuré seulement
 , et avec les hexapôles
, et avec les hexapôles 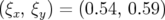 . Ces valeurs sont très différentes de celles
énoncées précédemment.
. Ces valeurs sont très différentes de celles
énoncées précédemment.
Ajoutons encore que la localisation des correcteurs dans les quadripôles implique un faible
recouvrement des intégrales de champ ; donc théoriquement le champ magnétique du correcteur
induit une modification de celui du quadripôle, de l’hexapôle. De plus, comme il y a une orbite
fermée non nulle, la perturbation créée par le dipôle n’est pas parfaitement dipolaire. Toutes ces
considérations n’ont pas été prises en compte dans notre simulation de la matrice-réponse et
pourraient expliquer les difficultés rencontrées pour réduire les données lorsque les hexapôles sont
allumés.
5.1.6.3 Dispersion mesurée dans les BPM
Les résultats sont résumés par la figure 5.17 et le tableau 5.10.
-
Régions non dispersives
- valeur attendue :
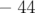 mm, l’écart modèle/expérience est grand,
en moyenne de 50%. Pour le BPM 9, la dispersion est pathologique,
mm, l’écart modèle/expérience est grand,
en moyenne de 50%. Pour le BPM 9, la dispersion est pathologique, 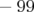 mm, soit le
double de celle des autres BPM.
mm, soit le
double de celle des autres BPM.
-
Régions dispersives
- valeur attendue :
 mm, l’écart modèle/expérience est
inférieur à 5%.
mm, l’écart modèle/expérience est
inférieur à 5%.
|
|
|
| | BPM1 | -48 | BPM09 | -99 |
| BPM2 | 1266 | BPM10 | 1286 |
| BPM3 | 1246 | BPM11 | 1239 |
| BPM4 | -64 | BPM12 | -64 |
| BPM5 | -59 | BPM13 | -60 |
| BPM6 | 1239 | BPM14 | 1259 |
| BPM7 | 1259 | BPM15 | 1243 |
| BPM8 | -68 | BPM16 | -52 |
|
|
|
| | |
| TAB. 5.10: | Dispersion horizontale mesurée (à 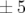 mm) — hexapôles allumés et onduleurs
ouverts — Les écarts relatifs sont plus importants dans les régions non dispersives (BPM 1,
4, 5, 8, 9, 12, 13 et 16 de Super-ACO). mm) — hexapôles allumés et onduleurs
ouverts — Les écarts relatifs sont plus importants dans les régions non dispersives (BPM 1,
4, 5, 8, 9, 12, 13 et 16 de Super-ACO). |
|
La dispersion peut être créée (Nadji, 1992) :
- par des défauts d’orbite fermée (
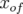 ) dans les quadripôles et les hexapôles :
) dans les quadripôles et les hexapôles :
- par les défauts de gradients (
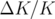 ) des quadripôles :
) des quadripôles :
Il est également intéressant de comparer ces valeurs de dispersion avec celles trouvées hexapôles
éteints (Fig. 5.18) : les dispersions ont changés de manière significative dans les régions à faible
dispersion bien que les valeurs des courants des familles Q3 et Q4, qui règlent la valeur de la
dispersion, n’aient pas changé entre les deux réglages optiques. Globalement les écarts relatifs sont
plus importants dans les régions à faible dispersion.
5.1.6.4 Résultats obtenus avec LOCO
Ajustement sur quatre familles :
En considérant les valeurs expérimentales hexapolaires déduites de courants mesurés, les écarts
rms entre matrices modèle et expérimentale valent  (H) et
(H) et 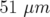 (V) avant
l’ajustement.
(V) avant
l’ajustement.
En symétrie 4, le résidu entre matrices modèle et expérimentale de Super-ACO est de 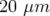 rms (H) et
rms (H) et 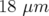 rms (V) avec un
rms (V) avec un 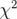 de 1 579. Le point de fonctionnement devient
de 1 579. Le point de fonctionnement devient
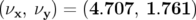 , ce qui est en accord avec les mesures expérimentales ; les gradients ont
changé de manière plus significative que dans le cas précédent (Fig. 5.19). Cette fois, la variation
sur les gradients est plus importante pour les familles Q1 et Q2 alors que dans le cas
hexapôles éteints il s’agissait plutôt de ceux de Q3 et Q4. On peut maintenant déduire les
gradients moyens induits par les hexapôles (Fig. 5.20) : les valeurs sont de l’ordre du pour
mille, i.e. extrêmement faibles. Les battements des fonctions
, ce qui est en accord avec les mesures expérimentales ; les gradients ont
changé de manière plus significative que dans le cas précédent (Fig. 5.19). Cette fois, la variation
sur les gradients est plus importante pour les familles Q1 et Q2 alors que dans le cas
hexapôles éteints il s’agissait plutôt de ceux de Q3 et Q4. On peut maintenant déduire les
gradients moyens induits par les hexapôles (Fig. 5.20) : les valeurs sont de l’ordre du pour
mille, i.e. extrêmement faibles. Les battements des fonctions 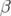 sont donnés par la
figure 5.21.
sont donnés par la
figure 5.21.
Ajustement sur les quadripôles individuels :
En faisant varier individuellement les gradients, les résidus deviennent : 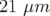 (H) et
(H) et 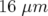 (V) dans chacun des plans avec un
(V) dans chacun des plans avec un 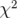 de 926. Les nombres d’ondes finaux valent :
de 926. Les nombres d’ondes finaux valent :
 .
.
Les défauts gradients mesurés sont donnés par la figure 5.22, les variations relatives vont
jusqu’à  . Ces variations sont similaires en termes d’amplitudes à celles trouvées hexapôles
éteints. Les battements des fonctions
. Ces variations sont similaires en termes d’amplitudes à celles trouvées hexapôles
éteints. Les battements des fonctions 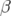 induits sont donnés à titre indicatif par la figure 5.25. En
utilisant la relation 5.17, il est possible possible d’extraire des défauts quadripolaires la contribution
hexapolaire (cf. Fig. 5.23) ainsi que le défaut d’orbite fermée dans les hexapôles (cf. Fig. 5.24). Ces
défauts sont relativement faibles. On remarque cependant que la distribution des défauts
d’orbite fermée horizontale n’est pas aléatoire : elle suit la 4-périodicité de l’anneau et est
corrélée aux mesures de la fonction dispersion dans les BPM et aux fonctions
induits sont donnés à titre indicatif par la figure 5.25. En
utilisant la relation 5.17, il est possible possible d’extraire des défauts quadripolaires la contribution
hexapolaire (cf. Fig. 5.23) ainsi que le défaut d’orbite fermée dans les hexapôles (cf. Fig. 5.24). Ces
défauts sont relativement faibles. On remarque cependant que la distribution des défauts
d’orbite fermée horizontale n’est pas aléatoire : elle suit la 4-périodicité de l’anneau et est
corrélée aux mesures de la fonction dispersion dans les BPM et aux fonctions 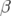 (cf.
Fig. 5.25).
(cf.
Fig. 5.25).
On peut encore remarquer que les valeurs de dispersions déduites de l’ajustement sont en
accord avec celles mesurés dans les BPM (Fig. 5.26). L’accord est meilleur lorsque l’on
compare les dispersions dans les correcteurs déduites de l’ajustement de 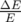 grâce à la
formule 5.9, et celles du modèle ajusté. Une des causes du désaccord moyen de 10% peut
être l’influence des erreurs dipolaires non modélisées (orbite fermée non nulle dans les
quadripôles).
grâce à la
formule 5.9, et celles du modèle ajusté. Une des causes du désaccord moyen de 10% peut
être l’influence des erreurs dipolaires non modélisées (orbite fermée non nulle dans les
quadripôles).
5.1.7 Matrice-réponse hexapôles allumés et onduleurs fermés
5.1.7.1 Conditions expérimentales
La matrice-réponse avec les onduleurs fermés a été acquise pour un courant  mA dans 24
paquets — dimensions faisceau
mA dans 24
paquets — dimensions faisceau  —. Les courants quadripolaires et
hexapolaires mesurés sont donnés par le tableau 5.11 ; les gradients des familles Q3 et Q4 ont été
modifiés pour compenser globalement la focalisation induite par les insertions.
—. Les courants quadripolaires et
hexapolaires mesurés sont donnés par le tableau 5.11 ; les gradients des familles Q3 et Q4 ont été
modifiés pour compenser globalement la focalisation induite par les insertions.
|
|
|
| | Famille | I(A) | Famille | I(A) |
|
|
|
| | Q1 | 218.50 | H1 | 54.35 |
| Q2 | 399.31 | H2 | 100.31 |
| Q3 | 377.88 | H3 | 198.58 |
| Q4 | 212.16 | H4 | 193.93 |
|
|
|
| | |
| TAB. 5.11: | Courants mesurés dans les
familles de quadripôles — hexapôles et
onduleurs fermés — Les courant des
familles Q1 et Q2 ont changé de manière
significative. Valeurs utilisées pour calibrer
le modèle de Super-ACO. |
|
|
Dans la version 8.15 de MAD, les onduleurs ne sont pas modélisables. L’ensemble des résultats
obtenus avec LOCO ne sera à prendre en compte que de manière qualitative. Cependant
l’ajustement ayant lieu principalement sur les fonctions optiques, les nombres d’ondes trouvés
seront très proches des valeurs expérimentales. Par contre, les variations sur les gradients
n’ont pas de signification physique, car ils ne tiennent pas compte de la focalisation des
onduleurs.
Si l’on considère une maille de Super-ACO avec les gradients quadripolaires et champs
hexapolaires mesurés via les courants mais sans onduleur, le point de fonctionnement vaut
 , qu’il faut ensuite modifier pour ajouter l’influence de la focalisation des
onduleurs.
, qu’il faut ensuite modifier pour ajouter l’influence de la focalisation des
onduleurs.
Les glissements des nombres d’ondes induits par l’ensemble des onduleurs (cf. Fig. 5.28) SU2,
SU3, SU6, SU7 et SU8 sont  . Ces valeurs calculées en utilisant
les valeurs expérimentales de courant (cf. Tab. 5.11) sont très proches des mesures réalisées au
début des années 1990 — Brunelle, 1992 — (cf. Tab. 5.12), le point de fonctionnement devient
après l’ajustement
. Ces valeurs calculées en utilisant
les valeurs expérimentales de courant (cf. Tab. 5.11) sont très proches des mesures réalisées au
début des années 1990 — Brunelle, 1992 — (cf. Tab. 5.12), le point de fonctionnement devient
après l’ajustement 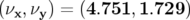 auquel il faudrait encore ajouter l’influence de l’orbite
fermée non nulle dans les hexapôles.
auquel il faudrait encore ajouter l’influence de l’orbite
fermée non nulle dans les hexapôles.
|
|
|
|
|
| | | SU2 | SU3 | SU6 | SU7 | SU8 |
|
|
|
|
|
| 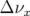 | 0.0053 | -0.007 | 0.0007 | 0.00 | -0.0016 |
 | 0.0477 | 0.046 | 0.0030 | 0.03 | 0.0275 |
|
|
|
|
|
| | |
| TAB. 5.12: | Glissement des nombres d’ondes expérimentaux induit par chacun des onduleurs.
Les onduleurs SU2, SU3, SU7 et SU8 vont le plus perturber l’optique de Super-ACO. |
|
Dans le code BETA [93], les onduleurs sont modélisés
idéalement,
i.e. sans focalisation horizontale ( et
et  ). Le point de fonctionnement déduit des
valeurs expérimentales de courant est alors
). Le point de fonctionnement déduit des
valeurs expérimentales de courant est alors 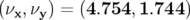 .
.
5.1.7.2 Dispersion mesurée dans les BPM
Les dispersions mesurées dans les BPM sont exprimées dans le tableau 5.13. Ne disposant pas de
modèle satisfaisant de l’anneau avec les onduleurs, on ne donnera pas de comparaison avec un
hypothétique modèle mais avec les valeurs mesurées de la fonction dispersion dans les deux cas
précédents (Fig. 5.29 et Fig. 5.30). La comparaison n’est donnée qu’à titre qualitatif puisque les
familles Q3 et Q4, réglant les dispersions, sont différentes. La grande différence concerne
la dispersion est maintenant positive dans les régions à faible dispersion (BPM 1, 4,
16) : en moyenne, les écarts relatifs sont de près de 150 % pour ces trois BPM. Par
contre dans les régions dispersives, les écarts relatifs restent faibles : inférieurs à  en
moyenne.
en
moyenne.
|
|
|
| | BPM1 | 52 | BPM09 | -92 |
| BPM2 | 1199 | BPM10 | 1331 |
| BPM3 | 1215 | BPM11 | 1279 |
| BPM4 | 24 | BPM12 | -76 |
| BPM5 | -44 | BPM13 | -12 |
| BPM6 | 1235 | BPM14 | 1235 |
| BPM7 | 1287 | BPM15 | 1179 |
| BPM8 | -72 | BPM16 | 20 |
|
|
|
| | |
| TAB. 5.13: | Dispersion horizontale mesurée (à  mm) dans les BPM de Super-ACO —
hexapôles allumés, onduleurs fermés — La fonction dispersion dans les régions non dispersives
a beaucoup changé. Dans les BPM 1, 4 et 16, la fonction dispersion est maintenant positive. mm) dans les BPM de Super-ACO —
hexapôles allumés, onduleurs fermés — La fonction dispersion dans les régions non dispersives
a beaucoup changé. Dans les BPM 1, 4 et 16, la fonction dispersion est maintenant positive. |
|
-
Régions non dispersives
- l’écart modèle-mesure est en moyenne de 45%.
-
Régions dispersives
- l’écart modèle-mesure est en moyenne de 5%.
5.1.7.3 Résultats obtenus avec LOCO
Tous les résultats suivants doivent être considérés qualitativement. L’algorithme LOCO converge
bien dans les deux plans avec des écarts 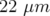 (H) et
(H) et  (V) et un point de fonctionnement
de
(V) et un point de fonctionnement
de  . L’allure des fonctions
. L’allure des fonctions 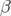 (Fig. 5.32) est déformée en particulier au
voisinage des onduleurs. Qualitativement, elle est en accord avec celle prédite par le code BETA.
Retenons simplement, que LOCO donne une bonne estimation de l’allure des fonctions optiques et
des nombres d’ondes. La perturbation de l’optique linéaire par les onduleurs SU2, SU3, SU7 et SU8
est nettement observée.
(Fig. 5.32) est déformée en particulier au
voisinage des onduleurs. Qualitativement, elle est en accord avec celle prédite par le code BETA.
Retenons simplement, que LOCO donne une bonne estimation de l’allure des fonctions optiques et
des nombres d’ondes. La perturbation de l’optique linéaire par les onduleurs SU2, SU3, SU7 et SU8
est nettement observée.
A titre indicatif, les variations sur les gradients sont données par la figure 5.31 : les écarts sont
de plusieurs pour cent. Comme les onduleurs ne sont pas inclus dans la description de la maille
utilisée par le code LOCO, ces valeurs ne doivent pas être considérées comme réalistes. Par contre,
il est intéressant de comprendre comment le programme LOCO a ajusté l’optique linéaire de
l’anneau de stockage.
Nous avons vu que les onduleurs induisent des glissements importants des nombres d’ondes en
particulier dans le plan vertical (cf. Tab. 5.12) ; les onduleurs SU2, SU3, SU7 et SU8 perturbent
fortement l’optique de Super-ACO. Le code LOCO compense localement la perturbation de chaque
onduleur en modifiant les gradients des quadripôles adjacents dont la focalisation est verticale. C’est
pourquoi, des variations relatives de plusieurs pour cent sont observées. En pratique,
l’influence des onduleurs est compensée globalement sauf pour SU8 (Brunelle et al.,
1999).
Conclusion
Ce travail a permis d’obtenir une estimation des erreurs quadripolaires mesurées pour deux
configurations machine à savoir hexapôles éteints et allumés. Deux approches ont été
tentées.
- La première, la plus naturelle, consistait à réaliser l’ajustement des matrices-réponse sur les
quatre familles quadripolaires puisque tous les quadripôles d’une même famille sont branchés
sur une même alimentation. Dans ce cas, la convergence du programme LOCO est
excellente.
- Hexapôles éteints, les défauts de gradients,
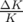 , sont faibles :
, sont faibles :  (Q1),
(Q1),
 (Q2) et
(Q2) et 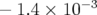 (Q3 et Q4). L’origine principale proviendrait des
courants des alimentations.
(Q3 et Q4). L’origine principale proviendrait des
courants des alimentations.
- Hexapôles allumés, la répartition globale des défauts de gradient a changé :
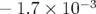 (Q1),
(Q1), 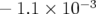 (Q2),
(Q2),  (Q3) et
(Q3) et 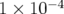 (Q4). Ces
variations s’expliquent par le terme quadripolaire engendré dans les hexapôles lorsque
l’orbite fermée est non nulle.
(Q4). Ces
variations s’expliquent par le terme quadripolaire engendré dans les hexapôles lorsque
l’orbite fermée est non nulle.
- Ces résultats peuvent être utilisés pour tenter d’améliorer la symétrie de l’anneau de
stockage. Il suffit d’alimenter chaque famille de quadripôle avec un courant corrigé des
écarts sur les gradients déduits du code LOCO (voir par exemple, Robin, Safranek et
Decking, 1999).
Les légers désaccords de la fonction dispersion dans les correcteurs proviennent en
majeure partie des défauts dipolaires qui n’ont pas été pris en compte dans cette
étude.
- Dans la seconde approche, on recherchait la distribution des gradients individuels pour estimer
quel est l’impact de la destruction de la symétrie 4 de l’anneau sur la dynamique globale du
faisceau.
Il s’est avéré que la convergence de l’algorithme est correcte seulement si l’on ne conserve que
les 16 valeurs singulières principales. Il semble exister une faible corrélation entre les
32 quadripôles individuels rendant leurs variations non indépendantes. De plus,
pour Super-ACO, les 32 gradients sont ajustés en utilisant 32 correcteurs et 32
lectures BPM. Pour une machine comme l’Advanced Light Source, l’ajustement est
typiquement fait sur 49 gradients et utilisant 96 BPM et 164 correcteurs. Le nombre
de stations de mesures de Super-ACO est trop faible pour espérer obtenir une
détermination des gradients individuels. A cela, il faut ajouter la faible résolution des
BPM.
Les déviations trouvées pour les gradients sont faibles, de l’ordre du pour mille. Ce résultat
est en accord avec les mesures magnétiques. Ce qui suggère que l’optique linéaire de
Super-ACO est bien modélisée. La compensation individuelle des défauts quadripolaires n’a
pas pu être vérifiée expérimentalement, car les quadripôles sont alimentés par
famille.
Pour ce qui est de l’influence des erreurs sur ces résultats énoncés, il convient de distinguer les
erreurs aléatoires des erreurs systématiques :
- Les erreurs aléatoires ne peuvent être estimées qu’en enregistrant régulièrement les
matrices-réponse pour une même configuration machine. De plus, la résolution des BPM
peut être améliorée si pour chaque mesure de la matrice-réponse, les données sont
moyennées sur plusieurs tours. Cette méthode a été utilisée avec succès à l’ALS : après
moyennisation, la résolution des BPM est descendue de 10
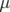 m à environ
m à environ 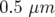 (communication personnelle, C. Steier).
(communication personnelle, C. Steier).
- Les erreurs systématiques sont en pratique minimisées par le choix de la force des
correcteurs. L’influence des nonlinéarités n’est cependant pas complètement supprimée.
On peut également s’interroger sur l’influence des quadripôles combinés de Super-ACO.
Nous pouvons également noter que nous avons obtenu les premières mesures expérimentales
qualitatives des fonctions optiques lorsque les onduleurs sont fermés. Pour prendre réellement en
compte l’effet des insertions, un travail possible consisterait à interfacer le code LOCO avec le code
BETA utilisé à Super-ACO.
Enfin, remarquons que le programme LOCO permet également de déduire le couplage de la
machine en analysant les matrices-réponse couplées. Cependant des perturbations dipolaires de
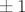 A, utilisées ici pour enregistrer les matrices-réponse, sont trop faibles pour observer des
termes croisés de la matrice-réponse non nuls compte tenu de la faible résolution des
BPM.
A, utilisées ici pour enregistrer les matrices-réponse, sont trop faibles pour observer des
termes croisés de la matrice-réponse non nuls compte tenu de la faible résolution des
BPM.
L’impact de ces résultats sur la compréhension de la dynamique de Super-ACO est faible. Les
défauts quadripolaires déduits sont de l’ordre de grandeur de ceux déduits des mesures
magnétiques. Or, nous avons vu que l’influence de ces derniers est très faible sur la dynamique du
faisceau (cf. chap. 3, section 3.2). Nous avons donc orienté notre recherche dans une autre
direction : la mesure expérimentale des glissements des nombres d’ondes avec l’amplitude
horizontale en utilisant des mesures tour par tour. Il est important de noter que l’anneau
Super-ACO ne dispose pas de BPM tour par tour ; il est équipé uniquement d’un perturbateur
horizontal.
5.2 Glissements expérimentaux des nombres d’ondes
Résumé
Le but de cette expérience est de mesurer le glissement des nombres d’ondes avec l’amplitude
horizontale afin de caractériser les nonlinéarités de la machine réelle. Une électrode située dans
la première section droite de l’anneau est utilisée pour réaliser des mesures tour par
tour. Dans un premier temps, on effectue un étalonnage de l’électrode au moyen de
déplacements horizontaux (bumps statiques). Puis avec l’aide d’un perturbateur (P4 ou P6),
on déplace le faisceau sur un tour et on le laisse osciller bétatroniquement. Le signal
collecté sur l’électrode est ensuite analysé en utilisant l’algorithme d’Analyse en Fréquence
(Laskar, 1990) dont la convergence rapide permet la détermination de fréquences sur
quelques centaines de tours. Ces mesures sont faites pour la machine nominale, onduleurs
ouverts, ainsi que pour une optique fortement détériorée (les familles hexapolaires H1
et H2 éteintes) où le phénomène de décohérence est dominant. Les premières courbes
expérimentales de la variation des nombres d’ondes avec l’amplitude sont présentées.
Le principal résultat est la mise en évidence d’une composante non modélisée de type
octupolaire.
5.2.1 Etalonnage de l’électrode à 45 degrés
- L’étalonnage de l’électrode dite « à 45 degrés », est réalisé au moyen d’un bump
statique
horizontal dans la première section droite de l’anneau, appelée SD1 (cf. Fig. 5.33), dont
l’amplitude varie entre
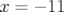 mm et
mm et  mm par pas de 1 mm environ.
mm par pas de 1 mm environ.
- Les nombres d’ondes sont rattrapés si nécessaire.
- Les onduleurs sont ouverts.
- Le couplage est augmenté à 100 % — en se mettant sur la résonance de couplage — pour allonger la durée de
vie de
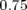 h à
h à  h (cf. paramètres Tab. 5.14).
h (cf. paramètres Tab. 5.14).
- Le signal lu sur l’électrode est moyenné et normalisé par le courant.
- L’amplitude du signal est plus grande pour un bump positif que négatif car l’électrode est localisée du coté
extérieur de l’anneau.
- A courant nul, le signal sur l’électrode vaut en moyenne 26 (en unités arbitraires), quantité retranchée par la
suite à toutes les mesures.
- La figure 5.34 donne une correspondance entre le signal normalisé par le courant lu sur l’électrode et
l’amplitude du bump, alors que la figure 5.35 illustre l’écart entre l’amplitude du bump lue en salle de contrôle
et l’amplitude effective du bump statique :
- Entre -4 et 2 mm, les valeurs du bump lues sur la console et sur l’électrode correspondent
parfaitement.
- Au-delà de 2 mm, on observe des différences jusqu’à 0.5 mm et une saturation à partir de 8.9 mm.
- Pour des bumps négatifs, les écarts sont plus importants puisque pour un bump de -8 mm, on lit un
déplacement d’orbite fermée de -7 mm, soit un écart de 1 mm ; la saturation est atteinte pour -8.84
mm.
- A grande amplitude, l’électronique n’est pas symétrique pour des bumps positifs et négatifs.
- La relation entre l’amplitude (
 ) et le signal normalisé (
) et le signal normalisé ( ) de l’électrode à 45 degrés suit une loi
quasi-linéaire entre -7 et +6 mm :
) de l’électrode à 45 degrés suit une loi
quasi-linéaire entre -7 et +6 mm :
![x[mm ] = 2.8× S[mA −1]− 27.95](these2142x.png) | (5.20) |
5.2.2 Utilisation de l’électrode à 45 degrés : point de fonctionnement nominal
Pour chaque kick du perturbateur (aimant dipolaire rapide), on maintient la phase constante par
rapport à la synchronisation de référence à des fins de reproductibilité. Les signaux de l’électrode et
du perturbateur sont enregistrés tour par tour.
5.2.2.1 Kick avec le perturbateur P4
- Les kicks du perturbateur P4 ont des amplitudes réparties entre 4.48 kV (butée basse
en tension du perturbateur) et 13.02 kV (début perte du faisceau) avec un pas d’environ
0.5 kV.
- Le courant stocké dans le paquet est de 9.3 mA tout au long de l’expérience.
- Le minimum de couplage n’a pas été réalisé (cf. conditions expérimentales Tab. 5.15).
Signal du perturbateur P4
- L’échantillonneur s’est déclenché un tour plus tôt (130-ème) pour les deux plus faibles
amplitudes (cf. Fig. 5.36).
- Le kick n’est pas sur un seul tour mais sur quatre (lié au principe d’injection à
Super-ACO).
- On observe un espacement régulier des amplitudes sur le perturbateur P4 : linéarité
tension-amplitude.
Signal sur l’électrode
5.2.2.2 Kick avec le perturbateur P6
- L’expérience précédente est refaite en utilisant le perturbateur P6 et en faisant le
minimum de couplage (cf. paramètres Tab. 5.17).
- Les amplitudes des kicks vont de
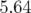 kV (butée basse) à
kV (butée basse) à 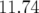 kV (début perte du
faisceau) par pas de 0.5 kV environ.
kV (début perte du
faisceau) par pas de 0.5 kV environ.
- Le courant varie de 8.3 mA à 7.3 mA au cours des mesures.
Signal sur perturbateur P6
- Les deux premiers kicks ont presque la même amplitude (Fig. 5.43).
- L’échantillonneur se déclenche au 129-ème tour à chaque fois.
- On observe un espacement régulier des amplitudes sur P6 : linéarité tension-amplitude.
- En théorie, les perturbateurs P4 et P6 sont identiques cependant :
- pour une même tension, le perturbateur P6 donne une amplitude plus grande au faisceau
(cf. Fig. 5.44). La loi de conversion entre la tension de P4 et P6, à amplitude constante,
est :
![VP 6 ≈ VP 4 + 0.65 [kV ]](these2222x.png) | (5.26) |
- la limite de l’ouverture dynamique est atteinte avec une amplitude plus faible (11.74 kV)
pour le perturbateur P6 que pour le perturbateur P4 (13.02 kV). Cet écart ne peut
pas s’expliquer uniquement par le point précédent, il est également nécessaire
que les paramètres de Twiss soient distincts dans les sections droites SD4 et
SD6.
Signal sur l’électrode
- Le nombre d’ondes vertical n’est plus observé, car le minimum de couplage est réalisé.
- En comparant les deux courbes en fréquence
 obtenues après perturbation du
faisceau avec P4 et P6 et après correction des tensions, on observe que les courbes ne
se superposent pas (Fig. 5.45).
obtenues après perturbation du
faisceau avec P4 et P6 et après correction des tensions, on observe que les courbes ne
se superposent pas (Fig. 5.45).
- Le nombre d’ondes horizontal doit suivre la même loi de variation qu’avec le perturbateur P4,
car les expériences réalisées avec les deux perturbateurs sont identiques ; les deux courbes en
fréquence sont superposables (Fig. 5.46) si l’on admet une nouvelle correction de la loi de
conversion (Eq. 5.26) :
![VP 6 ≈ VP4 + 0.65 + 0.95 [kV ]](these2224x.png) | (5.27) |
5.2.2.3 Utilisation de l’électrode à 45 degrés : familles H1 et H2 éteintes
- On a éteint les familles d’hexapôles H1 et H2 afin d’augmenter la variation des nombres
d’ondes avec l’amplitude : l’ouverture dynamique est ainsi réduite et la décohérence du
faisceau plus rapide.
| TAB. 5.18: | Conditions expérimentales
utilisées pour ajuster le modèle de
Super-ACO. Valeurs des courants des
quadripôles tournés pour obtenir le
minimum de couplage. Les chromaticités
sont élevées dans les deux plans. |
|
|
- Le minimum de couplage est réalisé (cf. paramètres Tab. 5.18).
- On observe une fluctuation inexpliquée de l’orbite contrairement au cas précédent avec les
hexapôles allumés.
Signal sur perturbateur P4
- L’échantillonneur se déclenche au 129-ème tour pour les 3 premiers kicks et au 130-ème
pour les suivants.
- On observe un espacement régulier des amplitudes sur P4 : linéarité tension-amplitude.
- Le fait de prendre une même phase de 950, permet d’obtenir une parfaite reproductibilité
des kicks générés par le perturbateur P4 (comparer les figures 5.36 et 5.47).
Signal sur l’électrode
5.2.3 Vers un nouveau modèle de Super-ACO
5.2.3.1 Observations
Ces résultats constituent pour Super-ACO les premières mesures tour par tour ainsi que les
premières mesures de la variation des nombres d’ondes avec l’amplitude horizontale.
La modélisation actuelle de Super-ACO ne permet pas d’expliquer :
- le sens de variation de
 en fonction de
en fonction de  sans l’introduction d’une composante forte de
type octupolaire. Dans la présente étude, seuls les octupôles des quadripôles ont été
introduits. Cependant d’autres éléments magnétiques de l’anneau peuvent créer un
octupôle :
sans l’introduction d’une composante forte de
type octupolaire. Dans la présente étude, seuls les octupôles des quadripôles ont été
introduits. Cependant d’autres éléments magnétiques de l’anneau peuvent créer un
octupôle :
- les coins des dipôles créent un pseudo-octupôle mais il est pratiquement impossible
de déduire sa contribution expérimentale.
- les hexapôles mais leurs contributions doivent être plus faibles que celles provenant
des quadripôles. En effet la force de ces octupôles doit être proportionnelle à celle
des hexapôles. Or lorsque les familles H1 et H2, les deux familles hexapolaires les
plus fortes, sont éteintes la contribution générale octupolaire n’a pas besoin d’être
modifiée pour ajuster le modèle sur l’expérience.
- les champs de fuite des quadripôles (cf. infra).
- la pente du nombre d’ondes vertical,
 , fonction de l’amplitude horizontale. Une tentative
d’introduction d’un hexapôle tourné dans les quadripôles ne permet pas de résoudre ce
problème.
, fonction de l’amplitude horizontale. Une tentative
d’introduction d’un hexapôle tourné dans les quadripôles ne permet pas de résoudre ce
problème.
- les chromaticités mesurées ne sont pas en accord avec celles calculées en utilisant le
logiciel BETA. Cette différence doit certainement être expliquée en partie par
l’algorithme de calcul de la chromaticité qui est écrit pour les machines à grand rayon de
courbure : ce n’est pas le cas pour Super-ACO. Ce problème est connu dans la
littérature.
- le début de perte du faisceau vers
 mm.
mm.
5.2.3.2 Champs de fuite des quadripôles
Le problème majeur que nous souhaitons résoudre est de comprendre quelle est l’origine de la
composante octupolaire observée. La valeur proposée est trop importante pour pouvoir être
expliquée par la composante aléatoire des octupôles de défauts des hexapôles. Nous allons
montrer que les champs de fuite des quadripôles permettent d’expliquer les observations
expérimentales.
Théorie des perturbations et glissements des nombres d’ondes : L’expression des champs de
fuite a déjà été étudiée par de nombreux auteurs. Sa formulation générale peut être
déduite de l’expression générale du champ magnétique en partant des équations de
Maxwell — voir par exemple, l’article complet de Papaphilippou, Wei et Talman (2001)
—.
Pour calculer le glissement des nombres d’ondes induits par les champs
de fuite du quadripôles, nous utilisons une théorie de perturbation. Nous
admettons la forme de la perturbation 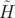 qui a été établie rigoureusement par
Zimmermann
(2000) pour un quadripôle dont les champs de fuite s’étendent de part et d’autre de l’aimant sur
une longueur
qui a été établie rigoureusement par
Zimmermann
(2000) pour un quadripôle dont les champs de fuite s’étendent de part et d’autre de l’aimant sur
une longueur  :
:
 | (5.31) |
avec en coordonnées rectangulaires, en ne gardant que les termes significatifs :
![{ ˜ -1 4 2 2 4
H1 ≈ 12(KQlQ )KQ [x + 6x y + y ]
˜H2 ≈ 152Δ2K2Q (KQlQ )[x4 − y4]](these2279x.png) | (5.32) |
où 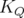 est le gradient du quadripôle et
est le gradient du quadripôle et  sa longueur effective.
sa longueur effective.
En utilisant les variables angles-actions,  et
et  , le
Hamiltonien moyenné devient en sommant sur tous les quadripôles de la machine (Zimmermann,
2000) :
, le
Hamiltonien moyenné devient en sommant sur tous les quadripôles de la machine (Zimmermann,
2000) :
< 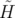 1 >≈ 1 >≈ |  ∑
Q(KQlQ)KQ[βx,Q2I
x2 + 4β
x,Qβy,QIxIy + βy,Q2I
y2] ∑
Q(KQlQ)KQ[βx,Q2I
x2 + 4β
x,Qβy,QIxIy + βy,Q2I
y2] | |
|
| +  ∑
QΔ2K
Q2(K
QlQ)[βx,Q2I
x2 − β
y,Q2I
y2] ∑
QΔ2K
Q2(K
QlQ)[βx,Q2I
x2 − β
y,Q2I
y2] | (5.33) |
Les glissements nombres d’ondes s’obtiennent par définition en dérivant 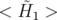 par rapport aux
actions
par rapport aux
actions 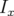 et
et  :
:
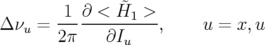 | (5.34) |
soit :
![1 ∑ 2 5 ∑ 2 2 2
Δ νx ≈ --- (KQlQ )KQ [βx,QIx + 2 βx,Q βy,QIy] + --- Δ KQ (KQlQ )βx,QIx
8 π Q 8π Q](these2291x.png) | (5.35) |
et :
![1 ∑ 5 ∑
Δ νy ≈ --- (KQlQ )KQ [β2y,QIy + 2 βx,Qβy,QIx] − --- Δ2K2Q (KQlQ )β2y,QIy
8 π Q 8π Q](these2292x.png) | (5.36) |
Application à Super-ACO : Pour Super-ACO, en prenant pour les applications numériques
 m,
m, 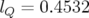 m et les valeurs expérimentales des gradients des quadripôles (cf.
Tab. 5.42), les glissements des nombres d’ondes sont :
m et les valeurs expérimentales des gradients des quadripôles (cf.
Tab. 5.42), les glissements des nombres d’ondes sont :
 | (5.37) |
où 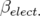 est l’expression de la fonction
est l’expression de la fonction 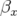 au niveau de l’électrode à 45 degrés.
La contribution des pseudo-octupôles des champs de fuite des quadripôles est tracée sur la
figure 5.52. La théorie et l’expérience sont en accord : les glissements des nombres d’ondes sont
pratiquement ceux mesurés. Il est également possible d’ajuster la composante pseudo-octupolaire
pour obtenir un accord parfait avec les mesures (cf. Fig. 5.52) :
au niveau de l’électrode à 45 degrés.
La contribution des pseudo-octupôles des champs de fuite des quadripôles est tracée sur la
figure 5.52. La théorie et l’expérience sont en accord : les glissements des nombres d’ondes sont
pratiquement ceux mesurés. Il est également possible d’ajuster la composante pseudo-octupolaire
pour obtenir un accord parfait avec les mesures (cf. Fig. 5.52) :
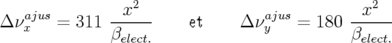 | (5.38) |
Les écarts entre les valeurs de ces glissements de nombres d’ondes théoriques et mesurés sont de
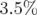 pour
pour 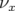 et
et 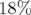 pour
pour 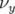 . Ces résultats sont compatibles avec l’incertitude sur les
valeurs expérimentales des fonctions
. Ces résultats sont compatibles avec l’incertitude sur les
valeurs expérimentales des fonctions 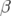 (perturbation de l’optique linéaire et couplage non
modélisés).
(perturbation de l’optique linéaire et couplage non
modélisés).
Modélisation en algèbre de Lie : Il est possible de modéliser ces champs de fuite en utilisant
l’algèbre de Lie. En 1998, Forest et Milutinović ont établi l’expression de l’application de
transfert 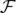 du champ de fuite, pour un quadripôle de gradient
du champ de fuite, pour un quadripôle de gradient  (voir aussi Forest,
1998) :
(voir aussi Forest,
1998) :
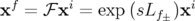 | (5.39) |
avec  .
.
 | (5.40) |
avec  ,
,  et
et  les couples de variables canoniques.
les couples de variables canoniques.
5.2.3.3 Conséquences sur la dynamique globale
Pour illustrer l’influence de la contribution des
pseudo-octupôles
sur la dynamique globale de Super-ACO, différentes cartes en fréquences de l’anneau ont été
calculées, accompagnées de la demi-ouverture dynamique correspondante.
-
1. Machine sans octupôle :
- Fig. 5.54 et Fig. B.6
Le point de fonctionnement  est le coin supérieur droit de
la carte. Le bord extérieur supérieur (resp. inférieur) correspond à la variation du
nombre d’ondes vertical avec
est le coin supérieur droit de
la carte. Le bord extérieur supérieur (resp. inférieur) correspond à la variation du
nombre d’ondes vertical avec 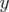 (resp. nombre d’ondes horizontal avec
(resp. nombre d’ondes horizontal avec  ). La carte
en fréquence est repliée sur elle-même. L’ouverture dynamique est réduite car les
chromaticités sont élevées dans les deux plans. La résonance
). La carte
en fréquence est repliée sur elle-même. L’ouverture dynamique est réduite car les
chromaticités sont élevées dans les deux plans. La résonance  est traversée à
grande amplitude,
est traversée à
grande amplitude, 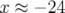 mm.
mm.
-
2. Machine avec octupôles :
- Fig. 5.55 et Fig. B.7
La carte en fréquence est complètement différente lorsqu’une composante octupolaire
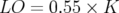 est introduite dans le modèle. Le sens de variation de
est introduite dans le modèle. Le sens de variation de 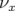 est inversé,
d’autres résonances apparaissent mais globalement leur coefficient d’excitation est assez
faible. Les dimensions de l’ouverture dynamique sont comparables au cas sans octupôle.
est inversé,
d’autres résonances apparaissent mais globalement leur coefficient d’excitation est assez
faible. Les dimensions de l’ouverture dynamique sont comparables au cas sans octupôle.
-
3. Machine avec octupôle, hexapôles H1 et H2 éteints :
- Fig. 5.56 et Fig. B.8
En éteignant les deux familles hexapolaires H1 et H2, le glissement des nombres
d’ondes est important avec l’amplitude, ce qui traduit une ouverture dynamique
diminuée dans les deux plans (réduction d’un facteur deux dans le plan horizontal).
Les résonances sont plus fortement excitées et la stabilité globale du faisceau est
détériorée.
-
4. Machine détériorée :
- Fig. 5.57 et Fig. B.9
Pour ce dernier cas, Super-ACO a été modélisé, toujours pour le point de fonctionnement de
routine, mais en augmentant la contribution octupolaire : 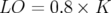 . Dans ce
cas, la dynamique est très fortement détériorée par l’excitation des différentes
résonances.
. Dans ce
cas, la dynamique est très fortement détériorée par l’excitation des différentes
résonances.
En particulier la résonance hexapolaire 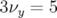 limite l’ouverture dynamique verticale
alors que la résonance
limite l’ouverture dynamique verticale
alors que la résonance  réduit son extension horizontale (voir aussi la
figure 5.58).
réduit son extension horizontale (voir aussi la
figure 5.58).
La carte en fréquence ainsi obtenue pourrait fortement refléter la dynamique réelle du faisceau
(en incluant par exemple les défauts de champs magnétiques). De plus, si la résonance
couplée 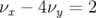 limitait expérimentalement la dynamique du faisceau, alors
l’ouverture dynamique serait réduite à
limitait expérimentalement la dynamique du faisceau, alors
l’ouverture dynamique serait réduite à 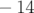 mm horizontalement et
mm horizontalement et  mm
verticalement.
mm
verticalement.
Rappelons enfin que tous ces résultats ont été obtenus en utilisant pour la première fois une
électrode à 45 degrés : de nombreux phénomènes parasites (bruit, méconnaissance de
l’étalonnage, réponse de l’électronique) sont venus perturber les mesures. Dans la section
suivante (5.3), nous présentons une confirmation de ces résultats : dans ce cas les mesures
sont effectués en utilisant une électrode d’un des BPM de l’anneau. Il sera extrêmement
intéressant de pouvoir refaire des expériences similaires dès que nous disposerons des
deux premiers BPM tour par tour qui devraient être installés début 2001 dans l’anneau
Super-ACO.
5.3 Espace des Phases et glissement des nombres d’ondes
Résumé
Lors de cette expérience, des données tour par tour ont été acquises pour déduire la variation des
nombres d’ondes  et
et 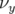 avec l’amplitude horizontale en utilisant l’Analyse en Fréquence
(Laskar, 1990). D’autre part, deux moniteurs de position sont utilisés pour réaliser les premières
mesures d’espaces des phases pour différentes configurations machine : point de fonctionnement de
routine avec et sans minimum de couplage, point de fonctionnement en éteignant les deux familles
d’hexapôles H1 et H2. Les résultats de l’expérience du 22 mai 2000 se trouvent confirmés, à savoir
l’existence d’une forte composante pseudo-octupolaire associée aux champs de fuite quadripolaires
non négligeables pour l’optique de Super-ACO.
avec l’amplitude horizontale en utilisant l’Analyse en Fréquence
(Laskar, 1990). D’autre part, deux moniteurs de position sont utilisés pour réaliser les premières
mesures d’espaces des phases pour différentes configurations machine : point de fonctionnement de
routine avec et sans minimum de couplage, point de fonctionnement en éteignant les deux familles
d’hexapôles H1 et H2. Les résultats de l’expérience du 22 mai 2000 se trouvent confirmés, à savoir
l’existence d’une forte composante pseudo-octupolaire associée aux champs de fuite quadripolaires
non négligeables pour l’optique de Super-ACO.
5.3.1 Etalonnage des BPM
5.3.1.1 Conditions expérimentales
- On travaille onduleurs ouverts, avec un courant
 mA dans un paquet. A la
suite d’un test avec le perturbateur P4 pour une tension de
mA dans un paquet. A la
suite d’un test avec le perturbateur P4 pour une tension de  kV, une grande partie
du faisceau a été perdue pour une raison inexpliquée. Pour cette expérience, il était
techniquement impossible d’injecter à nouveau du courant, on a donc continué de
travailler avec le courant
kV, une grande partie
du faisceau a été perdue pour une raison inexpliquée. Pour cette expérience, il était
techniquement impossible d’injecter à nouveau du courant, on a donc continué de
travailler avec le courant  mA.
mA.
- Les oscillations bétatrons sont collectées sur le bouton HE (Haut Extérieur [de l’anneau],
cf. Fig. 5.59) des BPM 12 et 4. Ce choix nous permet de conserver deux électrodes pour
la correction dipolaire verticale.
- Les deux BPM sont séparés par une avance de phase voisine non pas de
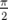 comme initialement désirée mais de
comme initialement désirée mais de  degrés (voir également le
synoptique de l’anneau Fig. 5.60). On pourra néanmoins obtenir une mesure
approximative
de l’espace des phases car si l’on appelle
degrés (voir également le
synoptique de l’anneau Fig. 5.60). On pourra néanmoins obtenir une mesure
approximative
de l’espace des phases car si l’on appelle 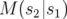 la matrice de transfert entre les deux
BPM, on peut alors écrire (Courant et Snyder, 1958) :
la matrice de transfert entre les deux
BPM, on peut alors écrire (Courant et Snyder, 1958) :
 | (5.41) |
avec 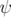 , la différence de phase entre les deux BPM et (
, la différence de phase entre les deux BPM et (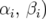 , les paramètres de Twiss en
, les paramètres de Twiss en
 . On en déduit immédiatement la relation :
. On en déduit immédiatement la relation :
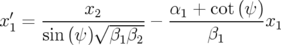 | (5.42) |
Pour un mouvement linéaire, les trajectoires sont des ellipses d’aire  où
où 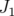 est l’action définie par
est l’action définie par 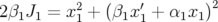 .
.
- Le point de fonctionnement est celui de routine avec des chromaticités légèrement plus élevées
(cf. paramètres expérimentaux Tab. 5.19).
- De manière générale, le signal est assez bruité. Cette perturbation est liée au fonctionnement
de l’accélérateur linéaire qui injectait un faisceau dans le second accélérateur : DCI (Dispositif
de Collisions dans l’Igloo).
5.3.1.2 Notes sur le BPM4
5.3.1.3 Notes sur le BPM12
- Pour le BPM 12, l’étalonnage est effectué pour des bumps statiques d’amplitude variant entre -12 mm
et +12 mm sans aucune incidence sur la durée de vie du faisceau (cf. infra pour l’explication de la
différence de comportement avec le BPM 4).
- Le signal résiduel moyen sans courant stocké est de
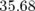 (u.a), quantité à retrancher aux mesures
ultérieures.
(u.a), quantité à retrancher aux mesures
ultérieures.
- La courbe de calibration du BPM12 est linéaire à la fois pour les valeurs mesurées directement sur
le bouton HE et lues en salle de contrôle, cependant les coefficients de proportionnalité ne sont pas
identiques (cf. Fig. 5.64).
- Les résultats sont vite en très grand désaccord : plus de
 mm à grande amplitude (cf. Fig. 5.65).
mm à grande amplitude (cf. Fig. 5.65).
- Les BPM 4 et 12 sont identiques en théorie, cependant leurs réponses diffèrent grandement.
5.3.2 Point de routine avec minimum de couplage
5.3.2.1 Conditions expérimentales
- On travaille avec le point de routine (cf. paramètres expérimentaux Tab. 5.20) en faisant
le minimum de couplage (réglage :
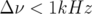 ).
).
- Un total de 13 mesures a été réalisé à la fois pour le BPM4 et pour le BPM12.
- La tension du perturbateur P4 varie entre 4.77 kV et 12.10 kV, le courant de 18.4 mA
à 16.7 mA.
- La décohérence est faible : plusieurs milliers de tours (cf. Fig. 5.66).
5.3.2.2 Espace des phases
5.3.2.3 Courbe en fréquence
avec  , la fonction
, la fonction  au niveau du moniteur de position.
au niveau du moniteur de position.
5.3.3 Point de routine avec couplage fort
5.3.3.1 Conditions expérimentales
- Pour ces mesures, le couplage est augmenté avec le quadripôle tourné QT4 ; l’ensemble
des paramètres expérimentaux est donné par le tableau 5.21.
- La tension du perturbateur P4 varie entre 4.77 kV (durée de vie :
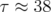 h) et 9.65 kV
(début de perte du faisceau,
h) et 9.65 kV
(début de perte du faisceau, 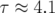 h), soit un total de 9 points de mesure pour les deux
BPM.
h), soit un total de 9 points de mesure pour les deux
BPM.
- Un exemple de signal collecté sur le BPM4 est illustré par la figure 5.72.
5.3.3.2 Espace des phases
- Comme précédemment, l’espace des phases est reconstruit en utilisant les coordonnées
de Courant-Snyder (cf. Fig. 5.73).
- La décohérence avec l’amplitude est plus importante, car le couplage est plus important ;
l’ouverture dynamique est réduite par rapport au précédent cas étudié (les nonlinéarités
sont plus importantes). En effet, on a vu que l’on commençait à perdre le faisceau dès
9.45 kV (contre 11.5 kV).
- Aux grandes amplitudes, les trajectoires sont fortement déformées : en calculant une
décomposition quasi-périodique pour cette orbite avec l’Analyse en Fréquence, la
présence de la résonance
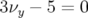 est mise en évidence.
est mise en évidence.
5.3.3.3 Courbes en fréquence
5.3.4 Familles H1 et H2 éteintes avec minimum de couplage
5.3.4.1 Conditions expérimentales
- Pour ces 9 mesures, le courant est environ de
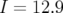 A (durée de vie :
A (durée de vie :  h),
le minimum de couplage est réalisé (QT4 fort), les chromaticités sont élevées dans les
deux plans (cf. Tab. 5.22).
h),
le minimum de couplage est réalisé (QT4 fort), les chromaticités sont élevées dans les
deux plans (cf. Tab. 5.22).
- La tension sur P4 varie de 4.70 kV à 9.58 kV (début perte du faisceau).
- La décohérence est importante, car d’une part, l’ouverture dynamique est plus petite
(le glissement des nombres d’ondes est plus importante) et d’autre part, la chromaticité
est importante dans les deux plans : le faisceau « décohère » complètement au bout de
600 tours à faible amplitude et de 150 tours à grande amplitude (cf. Fig. 5.75).
En pratique, seules les données avec un bon rapport signal-sur-bruit sont analysées.
Il s’ensuit une détérioration de la détermination des fréquences à grande amplitude.
Cependant, la convergence rapide de l’Analyse en Fréquence permet d’obtenir
amplement une précision du pour mille pour les nombres d’ondes.
5.3.4.2 Espace des phases
- L’espace des phases normalisé est reconstruit pour les différentes amplitudes de kicks
(cf. Fig. 5.76).
- La lisibilité des figures est rendue difficile par la décohérence rapide du faisceau. De
plus, comme le signal est collecté sur une unique électrode, les composantes verticale et
horizontale peuvent être mélangées.
- Les branches observées, par exemple pour
 kV, ne correspondent pas à des
résonances « dangereuses » mais traduisent simplement la rationalité du nombre d’ondes
(
kV, ne correspondent pas à des
résonances « dangereuses » mais traduisent simplement la rationalité du nombre d’ondes
( ).
).
5.3.4.3 Courbe en fréquence
5.3.5 Familles H1 et H2 éteintes sans minimum de couplage
5.3.5.1 Conditions expérimentales
- Seulement 6 mesures à un courant
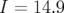 mA (durée de vie :
mA (durée de vie : 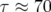 h) ont été
enregistrées, car l’ouverture dynamique est plus petite lorsque le minimum de couplage
n’est pas réalisé (cf. conditions expérimentales Tab. 5.23).
h) ont été
enregistrées, car l’ouverture dynamique est plus petite lorsque le minimum de couplage
n’est pas réalisé (cf. conditions expérimentales Tab. 5.23).
- La tension du perturbateur P4 varie de 4.77 kV à 7.82 kV (début de perte,
 h).
h).
- La décohérence est rapide : sur environ 500 tours à faible amplitude et 150 tours à
grande amplitude (cf. Fig. 5.78).
5.3.5.2 Espace des phases
- L’espace des phases normalisé est reconstruit comme précédemment en utilisant les
coordonnées de Courant-Snyder (cf. Fig. 5.79).
- On n’observe plus de branche sur les figures ; la décohérence du faisceau est plus rapide
que pour l’expérience précédente, car le couplage est plus important.
5.3.5.3 Courbes en fréquence
- Les deux nombres d’ondes sont extraits avec une précision plus faible puisque la décohérence
a lieu sur quelques centaines de tours.
- En utilisant les données du tableau 5.23 et les formules de glissement des nombres d’ondes
(Eq. 5.35 et Eq 5.36), la contribution des pseudo-octupôles au nombre d’ondes horizontal
s’écrit :
 | (5.50) |
avec  , la fonction
, la fonction 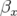 au niveau du moniteur de position.
au niveau du moniteur de position.
Dans le plan horizontal l’accord semble excellent et moindre pour le nombre d’ondes vertical
(cf. Fig.5.80).
- Notons qu’il est difficile d’ajuster de courbes avec seulement six points expérimentaux
correspondant à un faible variation du nombre d’ondes avec l’amplitude.
- Cependant, si expérimentalement le faisceau commence à être perdu pour une amplitude
d’environ 8 mm, le modèle avec un pseudo-octupôle prédit une ouverture dynamique
horizontal très proche à -10 mm.
5.3.6 Brève conclusion
Cette expérience a permis de mesurer pour la première fois, à Super-ACO, des espaces des
phases. Les données tour par tour ont été collectées sur une électrode de deux moniteurs
de positions de l’anneau. L’étalonnage et la comparaison des réponses des BPM 4 et
12 a montré qu’ils n’étaient pas équivalents avec des écarts jusqu’à 2 mm à grande
amplitude.
Le second volet de cette expérience a été l’analyse des données tour par tour pour déterminer
les glissements expérimentaux des nombres d’ondes transverses avec l’amplitude horizontale. Les
résultats confirment ceux obtenus lors de la première expérience de ce type (22 mai 2000) : les
champs de fuite des quadripôles produisent un terme pseudo-octupolaire fort qui perturbe fortement
la dynamique de l’anneau. En moyenne, les glissements des nombres d’ondes induits
sont :
Il faut noter que compte tenu des conditions expérimentales, des défauts non modélisés dans nos
simulations (erreurs dipolaires, défauts quadripolaires, couplage), ces résultats doivent être
accompagnés d’une barre d’erreur de l’ordre de dix pour cent.
5.4 Bilan et conclusion sur l’optique de Super-ACO
Les résultats expérimentaux présentés au cours de chapitre apportent un éclairage nouveau sur la
modélisation de Super-ACO. Pour améliorer la compréhension des performances actuelles de
l’anneau, nous souhaitions initier les premières mesures tour par tour des glissements des nombres
d’ondes avec l’amplitude sur l’anneau d’Orsay. Si à l’ALS il a été possible d’obtenir la première
carte en fréquence expérimentale d’un accélérateur, nous savions que la tâche serait plus ardue à
Super-ACO : l’anneau de stockage n’était pas équipé de BPM tour par tour et le faisceau ne
pouvait être déplacé que selon la direction horizontale. A la place des BPM tour par
tour, nous ne disposions que d’une électrode utilisée initialement pour le diagnostic et
mélangeant les signaux transverses. Cependant, ces expériences, innovantes à Orsay, ont suscité
un grand intérêt de la part de l’ensemble du groupe faisceau (conducteurs de faisceau,
électroniciens, ingénieurs, physiciens et techniciens). Une fois leur faisabilité technique
attestée, ces expériences ont presque toutes donné des résultats exploitables (à la grande
surprise de l’auteur). Utilisant l’Analyse en Fréquence, le principal résultat est la mise
en évidence expérimentale de l’influence des pseudo-octupôles des champs de fuite des
quadripôles de Super-ACO. Jusqu’à présent non pris en compte dans la modélisation de
l’anneau, nous avons vu qu’ils ont un impact considérable sur la dynamique transverse du
faisceau.
Ces résultats ont été confirmés depuis (printemps 2001). Deux « vrais » moniteurs
tour par tour ont été installés dans l’anneau de stockage pour refaire le même type
d’expériences. Ce travail a été réalisé en particulier par Mahdia Belgroune sous la direction
du groupe faisceau : bénéficiant d’une électronique plus rapide, d’un meilleur rapport
signal-sur-bruit, d’une meilleure résolution, les pseudo-octupôles permettent d’expliquer des
glissements des nombres d’ondes horizontal et vertical mesurés pour différents choix
d’optiques.
L’optique de Super-ACO peut désormais être modélisée par les éléments magnétiques
suivants :
- les dipôles avec les angles mesurés des coins et leurs champs de fuite de type hexapolaire
(Level et Nghiem, 1986) ;
- les quadripôles « combinés » :
- les quadripôles proprement dit, les erreurs de gradients ont peut d’impact sur la
dynamique (cf. matrices-réponse déduites avec le programme LOCO) ;
- les pseudo-octupôles associés aux champs de fuite des quadripôles (cf. mesures tour par tour
associées à l’Analyse en Fréquence). Pour le point de fonctionnement nominal, les
glissements des nombres d’ondes associés sont approximativement :
où  est la fonction optique au point d’observation.
est la fonction optique au point d’observation.
- leur composante dodécapolaire est négligeable pour des amplitudes inférieures à
20 mm. Leur force
 est liée à celle des quadripôles
est liée à celle des quadripôles 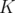 (Barthès et al.,
1990) :
(Barthès et al.,
1990) :
- les hexapôles (correction de la chromaticité et réduction des nonlinéarités).
- leur principal défaut multipolaire est une composante décapolaire dont la force
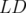 est
proportionnelle à la force hexapolaire
est
proportionnelle à la force hexapolaire  (Brunelle, 1999) :
(Brunelle, 1999) :
- leur composante octupolaire aléatoire peut être négligée (Barthès et al., 1990)
- les correcteurs (bobines dipolaires) peuvent être modélisé avec une composante hexapolaire
dans les sections dispersives. Ils contribuent à la chromaticité :
Ces valeurs ne sont pas figées, car la correction d’orbite fermée varie chaque jour ; seul
l’ordre de grandeur est à considérer.
- l’introduction d’autres multipôles (lentilles décapolaires des dipôles) a peut d’influence sur
la dynamique restreintes aux dimensions de l’ouverture physique.
- les quadripôles tournés, utilisés pour modifier le couplage, induisent un glissement du point
de fonctionnement. Typiquement pour l’optique nominale :
- les onduleurs n’ont pas été pris en compte dans la présente modélisation.
Le dernier point de désaccord observé concerne la mesure de la chromaticité naturelle. La raison
pourrait être simplement le logiciel BETA a été écrit pour des accélérateurs à grand rayon de
courbure. Un terme non négligeable pour le calcul de la chromaticité d’une machine telle
Super-ACO doit être bientôt introduit dans le code de calcul. De plus, les champs de fuite des
dipôles (non modélisés) sont de type hexapolaire et induisent une chromaticité verticale non
négligeable.
Enfin, l’intégrateur présenté dans la première partie de ce mémoire va prochainement être
utilisé pour d’une part vérifier l’assertion précédente au sujet de la chromaticité, et d’autre part
prendre en compte réellement les champs de fuite des quadripôles et, plus tard, les éléments
d’insertion.
Conclusions et perspectives
Au cours de ce travail, nous avons étudié une grande diversité de machines de rayonnement
synchrotron : Super-ACO avec ses 72 mètres de circonférence, l’ALS (196 mètres), SOLEIL (337
mètres) et l’ESRF (844 mètres). Suivant la taille de l’anneau, les approximations réalisées pour la
modélisation varient (termes des petites machines, coins des aimants, champs de fuite des éléments
magnétiques).
En utilisant le formalisme Hamiltonien, nous avons écrit un intégrateur des équations du
mouvement d’une particule relativiste. Chacun des principaux éléments magnétiques a été
modélisé par un Hamiltonien local à trois degrés de liberté. L’intégrateur utilise les méthodes
d’algèbre de Lie qui devraient connaître en Europe un développement comparable à celui des
Etats-Unis depuis leur introduction par A. Dragt. L’intégrateur proposé est un intégrateur
symplectique d’ordre quatre à pas tous positifs dont la précision est supérieure d’un ordre de
grandeur à l’intégrateur de Forest et Ruth.
L’Analyse en Fréquence a été notre principal outil d’investigation de la dynamique transverse
des accélérateurs. En calculant une carte en fréquence pour une optique donnée, nous obtenons une
vision globale de la dynamique du faisceau. L’allure des cartes en fréquence varie profondément
d’une machine à l’autre ; elle est très sensible aux réglages hexapolaires. De nombreuses
résonances d’ordre aussi bien faible qu’élevé détériorent la dynamique et induisent des
mouvements chaotiques. La convergence rapide, la précision de la méthode, l’utilisation de la
diffusion des orbites permettent également d’en faire un outil fiable pour prédire l’effet de
l’introduction des défauts magnétiques dans le modèle, du déplacement du point de
fonctionnement.
Nous avons vu qu’une fois connus, les défauts expérimentaux des gradients des quadripôles
droits et tournés d’un anneau (déduits des matrices-réponse), une carte en fréquence décrit une
dynamique très voisine de la dynamique réelle de l’accélérateur (taille de l’ouverture dynamique,
efficacité d’injection).
Une étape supplémentaire a été franchie en obtenant les premières cartes en fréquence
expérimentales d’un accélérateur. Les comparaisons avec le modèle théorique (de l’ALS) se sont
avérés remarquables en termes de glissements des nombres d’ondes avec l’amplitude,
de largeurs de résonance, de la diffusion des orbites au voisinage des nœuds entre les
résonances.
Les deux outils nécessaires pour réaliser de telles expériences sont un jeu de BPM tour par tour
et deux aimants rapides permettant de déplacer sur un seul tour le faisceau dans les plans horizontal
et vertical.
L’Analyse en Fréquence peut ainsi être directement intégrée comme un des outils de diagnostic
du faisceau dans la salle de contrôle d’un accélérateur. C’est déjà une réalité à l’Advanced Light
Source où une carte en fréquence peut être tracée de manière quasi-automatique. Pour rendre
l’utilisation de la méthode encore plus pratique, le système de mesure de l’ALS va être
prochainement modifié pour permettre l’acquisition d’une carte en fréquence en une vingtaine de
minutes.
A Super-ACO, même s’il était techniquement impossible d’obtenir une carte en fréquence, les
mesures tour par tour du glissement des nombres d’ondes avec l’amplitude ont permis de mettre en
évidence le fort effet des champs de fuites des quadripôles (non modélisé jusqu’à présent). Leur
inclusion dans le modèle de l’anneau révèle une dynamique entièrement différente et permet de
mieux comprendre les performances actuelles de la machine (ouverture dynamique, résonances,
réglages des hexapôles).
Les perspectives à la suite de ce travail sont nombreuses avec pour un des thèmes
principaux, l’association de l’Analyse en Fréquence et des mesures tour par tour dans un
accélérateur.
Ma courte expérience dans le monde des accélérateurs m’a convaincu du point essentiel suivant.
Les écarts sur les performances des sources de lumière entre les prédictions et les mesures
expérimentales sont très souvent proche d’un facteur deux. La raison principale est qu’il est
impossible d’obtenir une description absolue des champs magnétiques, des positionnements des
éléments dans l’anneau de stockage, de paramètres moins prévisibles (vibrations, marées solides,
variations de la température).
Ne pouvant tout prévoir, il est par contre primordiale de prévoir, dès la construction d’un
accélérateur (l’auteur pense en particulier au futur anneau de stockage SOLEIL), un grand nombre
d’outils de diagnostic, outils qui constituent littéralement les « yeux » et les « oreilles » du physicien
des accélérateurs. Ce sont en particulier des moniteurs de position tour par tour, des aimants
rapides pour déplacer le faisceau sur un tour.
Nous avons vu que les mesures expérimentales sont souvent compliquées par le phénomène de la
décohérence. Par exemple, le faisceau de l’ESRF « décohère » en une centaine de tours pour déjà de
très faibles déplacements horizontaux du faisceau. Pour un anneau de la taille de l’ESRF, il doit
être possible d’obtenir des données exploitables en modifiant la philosophie des mesures : au lieu
d’enregistrer le signal sur un BPM particulier de l’anneau tous les tours, l’utilisation conjointe de
l’ensemble des BPM doit permettre d’augmenter de manière significative l’échantillonnage des
données.
A l’ALS, l’Analyse en Fréquence est et sera pleinement utilisée pour caractériser l’impact des
trois aimants supraconducteurs qui vont être installés en août 2001 dans l’anneau et réduire sa
périodicité de douze à trois. Des résultats récents (Steier, Robin, Wu, Decking, Laskar et Nadolski,
2001) reposent sur l’utilisation de cet outil pour caractériser et comprendre les causes de limitations
de la dynamique off momentum de l’ALS.
Dans ce travail, l’Analyse en Fréquence a principalement été utilisée à travers les cartes en
fréquence, i.e. en ne conservant que le premier terme de la décomposition quasi-périodique obtenue
en analysant les trajectoires de phase. Une autre approche consiste à utiliser la décomposition
complète donnée par l’Analyse en Fréquence. L’amplitude de chaque terme correspond à
l’amplitude d’une résonance donnée. Il est ainsi possible d’extraire de nombreuses autres
informations sur la dynamique et d’obtenir une nouvelle méthode d’optimisation d’un
accélérateur.
Ces nouveaux développements devront être considérés pour permettre non seulement
d’améliorer les accélérateurs actuels mais aussi de concevoir les prochaines générations de
machines tels les sources de lumière de quatrième génération, les « usines à muon » et les
collisionneurs.
 , situé en
, situé en  , donnant un angle ou impulsion (kick en
anglais)
, donnant un angle ou impulsion (kick en
anglais)  à une particule, avec
à une particule, avec  la rigidité magnétique et
la rigidité magnétique et 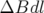 le champ
dipolaire intégré. Si juste avant l’impulsion, l’orbite fermée est
le champ
dipolaire intégré. Si juste avant l’impulsion, l’orbite fermée est  , alors juste après
l’impulsion, elle devient
, alors juste après
l’impulsion, elle devient  . Trouver l’expression de l’orbite fermée
. Trouver l’expression de l’orbite fermée 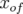 en
en 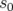 revient à
résoudre la relation de fermeture :
revient à
résoudre la relation de fermeture :
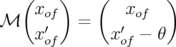
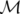 est la matrice de transfert de l’anneau sur un tour. La solution, exprimée en fonction des
paramètres de Twiss
est la matrice de transfert de l’anneau sur un tour. La solution, exprimée en fonction des
paramètres de Twiss 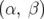 , du nombre d’ondes
, du nombre d’ondes  , est alors
, est alors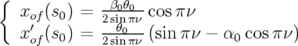
 quelconque de
l’anneau, il suffit de propager la solution trouvée en
quelconque de
l’anneau, il suffit de propager la solution trouvée en  en utilisant la fonction de Green,
en utilisant la fonction de Green,
 , de l’équation de Hill
, de l’équation de Hill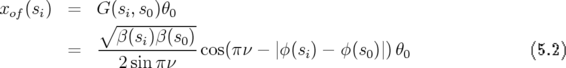
 , en utilisant la linéarité de l’équation de Hill en la
perturbation dipolaire, l’orbite fermée résultante est simplement la superposition des orbites
fermées individuelles créées par une impulsion
, en utilisant la linéarité de l’équation de Hill en la
perturbation dipolaire, l’orbite fermée résultante est simplement la superposition des orbites
fermées individuelles créées par une impulsion  (cf. Eq.
(cf. Eq. 
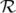 est appelée
est appelée  éléments pour une machine comportant
éléments pour une machine comportant  correcteurs dipolaires et
correcteurs dipolaires et 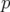 BPM (
BPM (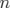 correcteurs et en
enregistrant dans chacun des
correcteurs et en
enregistrant dans chacun des 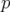 BPM l’orbite fermée générée.
BPM l’orbite fermée générée.
 et une
autre pour des
et une
autre pour des  . En effet, il subsiste une orbite fermée résiduelle créée par les
nonlinéarités des champs magnétiques. En calculant la différence de ces deux matrices, on élimine
ainsi l’orbite fermée résiduelle et l’on obtient une matrice-réponse équivalente à un
. En effet, il subsiste une orbite fermée résiduelle créée par les
nonlinéarités des champs magnétiques. En calculant la différence de ces deux matrices, on élimine
ainsi l’orbite fermée résiduelle et l’on obtient une matrice-réponse équivalente à un  .
.
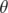 permet d’augmenter le rapport signal sur bruit de la mesure et donc
de réduire la barre d’erreur sur les valeurs de gradients trouvées par rapport au bruit aléatoire des
BPM
permet d’augmenter le rapport signal sur bruit de la mesure et donc
de réduire la barre d’erreur sur les valeurs de gradients trouvées par rapport au bruit aléatoire des
BPM permet de s’affranchir des nonlinéarités mais aussi de
rester dans une gamme de réponse linéaire de l’électronique. Une valeur intermédiaire doit donc
être choisie
permet de s’affranchir des nonlinéarités mais aussi de
rester dans une gamme de réponse linéaire de l’électronique. Une valeur intermédiaire doit donc
être choisie mm rms (valeur optimale pour le NSLS X-Ray Ring à Brookhaven
mm rms (valeur optimale pour le NSLS X-Ray Ring à Brookhaven mm rms — Safranek, 1997
—).
mm rms — Safranek, 1997
—).
 » entre
la matrice-réponse modèle,
» entre
la matrice-réponse modèle,  , et la matrice-réponse expérimentale,
, et la matrice-réponse expérimentale, 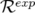 , en ajustant les
gradients quadripolaires
, en ajustant les
gradients quadripolaires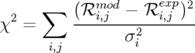
 et les correcteurs
et les correcteurs 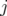 , normalisée par le bruit des BPM
, normalisée par le bruit des BPM  et
en utilisant une méthode de décomposition en valeurs singulières (SVD
et
en utilisant une méthode de décomposition en valeurs singulières (SVD 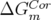 ), les gains des BPM (
), les gains des BPM ( ) et le glissement de
l’énergie (
) et le glissement de
l’énergie (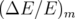 ). Pour la matrice couplée, il faut ajouter la rotation des BPM et des
correcteurs.
). Pour la matrice couplée, il faut ajouter la rotation des BPM et des
correcteurs.
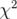 revient à minimiser la norme du vecteur
revient à minimiser la norme du vecteur  dont les composantes sont définies
par
dont les composantes sont définies
par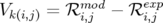
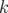 varie de
varie de  à
à 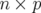 . Alors en approximation linéaire, on
obtient
. Alors en approximation linéaire, on
obtient
 est le nombre de degrés de liberté, soit
est le nombre de degrés de liberté, soit  avec un écart
type
avec un écart
type  avec
avec 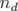 le nombre de données (taille du vecteur
le nombre de données (taille du vecteur  ) et
) et  le
nombre de paramètres ajustés (cf.
le
nombre de paramètres ajustés (cf. 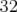 correcteurs,
correcteurs,  verticaux (dans les
quadripôles défocalisant,
verticaux (dans les
quadripôles défocalisant, 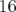 horizontaux (dans les
quadripôles focalisant,
horizontaux (dans les
quadripôles focalisant,  autres
correcteurs horizontaux, chacun situé dans un dipôle (non utilisés dans la présente
étude
autres
correcteurs horizontaux, chacun situé dans un dipôle (non utilisés dans la présente
étude BPM composés de quatre électrodes se trouvent dans chacun des doublets de
quadripôles (cf. maille Fig.
BPM composés de quatre électrodes se trouvent dans chacun des doublets de
quadripôles (cf. maille Fig. 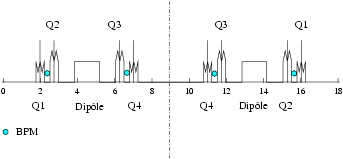
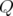 ) contient,
en plus du gradient quadripolaire, une
lentille décapolaire (
) contient,
en plus du gradient quadripolaire, une
lentille décapolaire ( ), un hexapôle
(
), un hexapôle
( ) et une bobine dipolaire appelée
) et une bobine dipolaire appelée

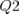

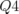
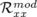
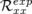





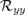
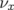
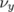
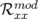


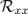




 de
chacune des 4 familles quadripolaires
de
chacune des 4 familles quadripolaires  de Super-ACO. Ces résultats ne donnent pas un
accord parfait compte tenu de la basse « résolution » (2 chiffres significatifs).
de Super-ACO. Ces résultats ne donnent pas un
accord parfait compte tenu de la basse « résolution » (2 chiffres significatifs).  et
et 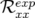 (resp.
(resp. 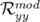 et
et 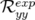 ) sont les valeurs rms en millimètres des matrices-réponse théorique et
expérimentale horizontales (resp. verticales).
) sont les valeurs rms en millimètres des matrices-réponse théorique et
expérimentale horizontales (resp. verticales). 
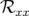 et
et 
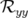 donnent l’écart rms entre
ces matrices.
donnent l’écart rms entre
ces matrices.
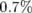


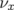

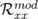


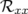
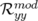
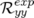

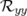
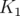 de la famille
quadripolaire
de la famille
quadripolaire 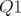 (en symétrie 4). Ecarts relatifs et convergence en prenant 8 chiffres
significatifs dans l’expression de la matrice-réponse. L’ajustement est « parfait ».
(en symétrie 4). Ecarts relatifs et convergence en prenant 8 chiffres
significatifs dans l’expression de la matrice-réponse. L’ajustement est « parfait ».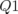

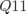



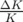

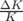
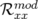
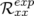


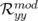
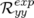

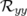
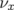
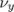
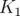 du premier
quadripôle
du premier
quadripôle  de Super-ACO (la symétrie 4 est brisée). Les écarts relatifs finaux pour les
gradients (
de Super-ACO (la symétrie 4 est brisée). Les écarts relatifs finaux pour les
gradients ( ) de 32 quadripôles (
) de 32 quadripôles (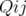 ) correspondent à la précision machine (8 chiffres
significatifs)
) correspondent à la précision machine (8 chiffres
significatifs) ainsi que les valeurs de bruit
rms,
ainsi que les valeurs de bruit
rms, 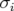 , pour les deux cas considérés. De manière générale, les valeurs de bruits sont plus élevées
en début qu’en fin d’expérience (Tab.
, pour les deux cas considérés. De manière générale, les valeurs de bruits sont plus élevées
en début qu’en fin d’expérience (Tab. 

 de Super-ACO dans les plans
vertical et horizontal (précision
de Super-ACO dans les plans
vertical et horizontal (précision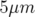 ). Les écarts entre les bruit pour 1 000 et 100 orbites
peuvent s’expliquer par le fait que dans un cas les onduleurs sont fermés et que le courant
stocké est différent.
). Les écarts entre les bruit pour 1 000 et 100 orbites
peuvent s’expliquer par le fait que dans un cas les onduleurs sont fermés et que le courant
stocké est différent. 
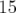
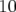
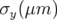


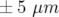 ).
).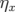 , dans les BPM est calculée avec la formule usuelle (Rice
, dans les BPM est calculée avec la formule usuelle (Rice 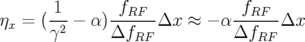
 , le facteur d’allongement du premier ordre (
, le facteur d’allongement du premier ordre (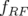 , la
fréquence RF de l’anneau. Pour cela, on réalise deux mesures d’orbite fermée (
, la
fréquence RF de l’anneau. Pour cela, on réalise deux mesures d’orbite fermée ( ), pour deux
fréquences RF distinctes (
), pour deux
fréquences RF distinctes ( ) juste avant l’acquisition de chacune des matrices-réponse (cf.
paramètres Tab.
) juste avant l’acquisition de chacune des matrices-réponse (cf.
paramètres Tab. ![δηx δα δfRF δ ΔfRF δΔx
---- = ---+ ----- + ------- + -----
ηx α fRF ΔfRF Δx
≈ δΔfRF--+ δΔx--
ΔfRF Δx
1
≈ 2.7 × 10− 4 + -------------- (5.8)
Δx [1∕100mm ]](these1941x.png)
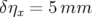 .
.



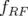
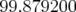
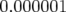
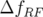
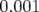
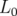
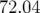

 BPM,
BPM, 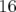 correcteurs horizontaux et 16 correcteurs verticaux, donc la
matrice-réponse non couplée a
correcteurs horizontaux et 16 correcteurs verticaux, donc la
matrice-réponse non couplée a 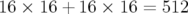 éléments.
éléments.
 , soit
approximativement
, soit
approximativement 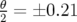 mrad pour un correcteur horizontal et
mrad pour un correcteur horizontal et  mrad pour un correcteur
vertical
mrad pour un correcteur
vertical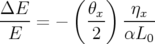
 le facteur d’allongement du premier ordre et
le facteur d’allongement du premier ordre et  la circonférence de la machine.
la circonférence de la machine.
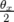 produite par le correcteur dipolaire engendre — si la fonction
dispersion
produite par le correcteur dipolaire engendre — si la fonction
dispersion 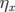 est non nulle — une modification de la longueur
est non nulle — une modification de la longueur 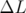 de l’orbite de la
particule
de l’orbite de la
particule
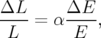
 mA dans 24 paquets, en
faisceau « plat »
mA dans 24 paquets, en
faisceau « plat »  , ceci avec les quatre familles d’hexapôles éteintes.
Cette possibilité d’éteindre les hexapôles avec un faisceau circulant dans l’anneau est un
avantage qui permettra de déterminer les défauts de gradients indépendamment de ceux
induits par les hexapôles lorsqu’il existe une orbite résiduelle
, ceci avec les quatre familles d’hexapôles éteintes.
Cette possibilité d’éteindre les hexapôles avec un faisceau circulant dans l’anneau est un
avantage qui permettra de déterminer les défauts de gradients indépendamment de ceux
induits par les hexapôles lorsqu’il existe une orbite résiduelle 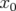 en leur centre (cf.
section
en leur centre (cf.
section  . Notons que par rapport au point de
fonctionnement nominal, le courant dans
. Notons que par rapport au point de
fonctionnement nominal, le courant dans  ayant changé, les valeurs de la fonction dispersion
théorique sont également légèrement modifiées. Les nombres d’ondes mesurés valent
ayant changé, les valeurs de la fonction dispersion
théorique sont également légèrement modifiées. Les nombres d’ondes mesurés valent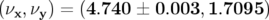 . L’incertitude sur
. L’incertitude sur  provient de la faible valeur du courant
provient de la faible valeur du courant
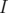 (à l’oscilloscope au lieu d’un pic unique, on en observe plusieurs).
(à l’oscilloscope au lieu d’un pic unique, on en observe plusieurs).
 mm
mm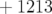 mm
mm mm) — hexapôles éteints et onduleurs ouverts — Les écarts relatifs sont plus importants
dans les régions non dispersives (BPM 1, 4, 5, 8, 9, 12, 13 et 16).
mm) — hexapôles éteints et onduleurs ouverts — Les écarts relatifs sont plus importants
dans les régions non dispersives (BPM 1, 4, 5, 8, 9, 12, 13 et 16).
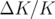 (cf. sous-section
(cf. sous-section ![∘ ---- [ ] 1
(Δ ηx)rms βx ∑ 2
------------ = -√------0---- βxi((Kl )iηxi)2 (5.12)
(ΔK ∕K )rms 2 2|sinπνx | i
≈ 20.4](these1984x.png)
 mm rms alors que la valeur issue des mesures expérimentales est presque
trois fois plus grande
mm rms alors que la valeur issue des mesures expérimentales est presque
trois fois plus grande  mm rms.
mm rms.
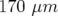 horizontalement (H) et à
horizontalement (H) et à 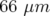 verticalement (V).
verticalement (V).
 (réduction
d’un facteur 5) et
(réduction
d’un facteur 5) et 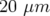 (réduction d’un facteur 3) respectivement dans les plans horizontal et
vertical avec un
(réduction d’un facteur 3) respectivement dans les plans horizontal et
vertical avec un  de 2 080. En suivant les résultats énoncés précédemment, la valeur escomptée
du
de 2 080. En suivant les résultats énoncés précédemment, la valeur escomptée
du 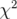 devrait être idéalement au mieux
devrait être idéalement au mieux 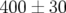 , sachant qu’il y a (
, sachant qu’il y a ( ) points de donnée
et (
) points de donnée
et ( ) paramètres indépendants ajustés. Le point de fonctionnement devient alors
) paramètres indépendants ajustés. Le point de fonctionnement devient alors
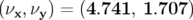 soit
soit  , ce qui est en excellent accord avec
la mesure expérimentale des nombres d’ondes. Les gradients des familles de quadripôles ont varié
de moins de
, ce qui est en excellent accord avec
la mesure expérimentale des nombres d’ondes. Les gradients des familles de quadripôles ont varié
de moins de 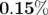 (cf. Tab.
(cf. Tab. 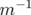 ) en symétrie 4 avant
et après l’ajustement de LOCO. Données
utilisées pour ajuster le modèle linéaire de
Super-ACO.
) en symétrie 4 avant
et après l’ajustement de LOCO. Données
utilisées pour ajuster le modèle linéaire de
Super-ACO.
 sont tracées sur la figure
sont tracées sur la figure 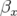 est de
est de  autour de
autour de 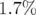 (traduit le glissement
(traduit le glissement  ) et celui de
) et celui de  est de
est de
 autour de
autour de  (
(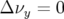 ).
).
 . Par contre dans le plan horizontal, la valeur attendue
. Par contre dans le plan horizontal, la valeur attendue 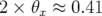 , n’est pas
atteinte dans les régions dispersives. Cet écart est à corréler avec l’écart en dispersion donné par
LOCO (cf. Fig.
, n’est pas
atteinte dans les régions dispersives. Cet écart est à corréler avec l’écart en dispersion donné par
LOCO (cf. Fig. 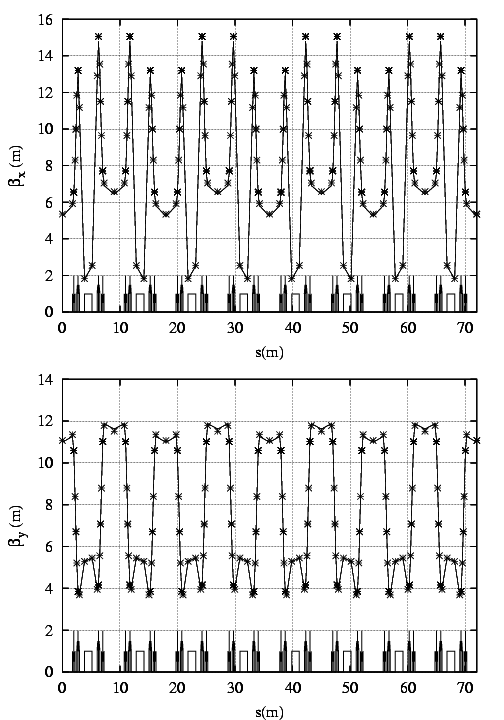
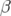 avant (ligne) et
après (étoile) l’ajustement en symétrie 4.
L’expérience s’ajuste parfaitement sur la
théorie, car les variations de gradients sont
faibles, de l’ordre du pour mille.
avant (ligne) et
après (étoile) l’ajustement en symétrie 4.
L’expérience s’ajuste parfaitement sur la
théorie, car les variations de gradients sont
faibles, de l’ordre du pour mille.
 en
conservant la symétrie 4 de Super-ACO.
en
conservant la symétrie 4 de Super-ACO.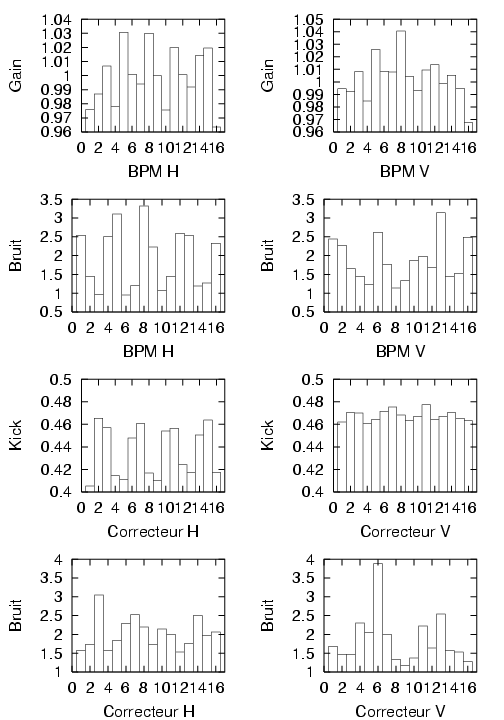
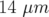 et
et 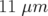 , horizontalement et verticalement
avec comme nombres d’ondes
, horizontalement et verticalement
avec comme nombres d’ondes 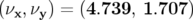 et un
et un  de
de 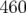 . Les gradients des
quadripôles ont varié de façon plus significative jusqu’à
. Les gradients des
quadripôles ont varié de façon plus significative jusqu’à  (Fig.
(Fig. 
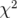 suggère, ou bien que la machine est parfaitement
connue, ou bien que le nombre de paramètres ajustés est trop important. La dernière
hypothèse semble la plus raisonnable
suggère, ou bien que la machine est parfaitement
connue, ou bien que le nombre de paramètres ajustés est trop important. La dernière
hypothèse semble la plus raisonnable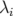 ) sont rangées par ordre décroissant de l’amplitude. On observe une
décroissance rapide des amplitudes avec deux seuils
) sont rangées par ordre décroissant de l’amplitude. On observe une
décroissance rapide des amplitudes avec deux seuils , le second en
, le second en 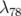 .
.

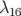 . Au-delà, les valeurs singulières sont petites, du même ordre de grandeur
. Au-delà, les valeurs singulières sont petites, du même ordre de grandeur (H) et
(H) et 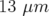 (V) avec comme nouveaux nombres
d’ondes
(V) avec comme nouveaux nombres
d’ondes 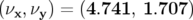 et un
et un 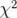 plus élevé de 1 050. La variation des gradients
individuels est aléatoire et avec des amplitudes très voisines de celles obtenues pour les familles de
quadripôles (Fig.
plus élevé de 1 050. La variation des gradients
individuels est aléatoire et avec des amplitudes très voisines de celles obtenues pour les familles de
quadripôles (Fig. 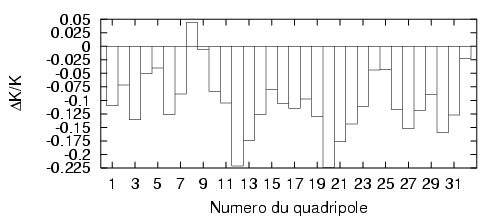

 sont tracées sur la figure
sont tracées sur la figure 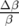 , sont plus importants horizontalement (
, sont plus importants horizontalement (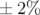 autour de
autour de 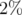 ) que
verticalement
) que
verticalement  . Ils s’expriment en première approximation suivant la formule classique
(Rice et Cornell
. Ils s’expriment en première approximation suivant la formule classique
(Rice et Cornell 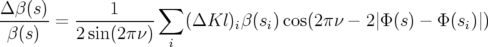
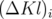 est le gradient intégré du i-ème quadripôle,
est le gradient intégré du i-ème quadripôle,  son avance de phase.
son avance de phase.
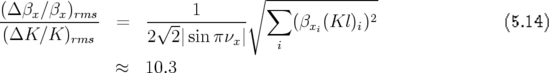
 , ce qui est en accord
avec la figure 5.14.
, ce qui est en accord
avec la figure 5.14.
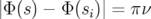 soit pour un défaut dans un quadripôle situé de manière diamétralement
opposée à la position
soit pour un défaut dans un quadripôle situé de manière diamétralement
opposée à la position  du BPM où il est observé.
du BPM où il est observé.
 rapporté au bruit total rms de tous les BPM n’est pas voisin de l’unité comme il
devrait l’être théoriquement pour une convergence atteignant le niveau de bruit des
BPM.
rapporté au bruit total rms de tous les BPM n’est pas voisin de l’unité comme il
devrait l’être théoriquement pour une convergence atteignant le niveau de bruit des
BPM.
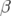 , les nombres d’ondes.
Les défauts de gradients trouvés sont relativement faibles, ce qui suggère un assez bon accord entre
la théorie et l’expérience.
, les nombres d’ondes.
Les défauts de gradients trouvés sont relativement faibles, ce qui suggère un assez bon accord entre
la théorie et l’expérience.
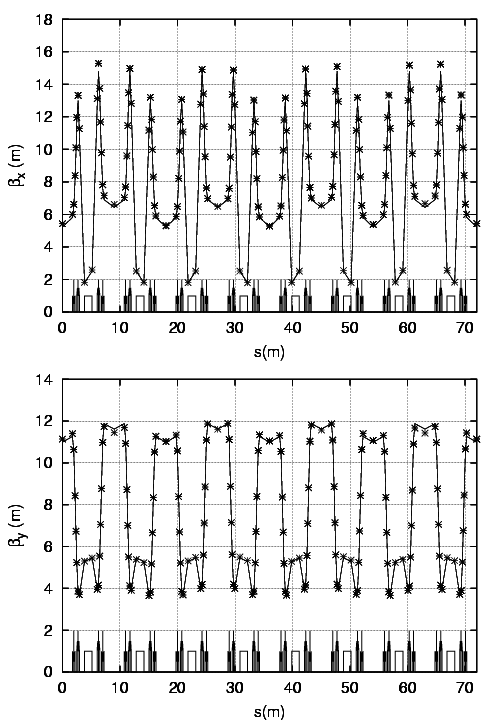
 de Super-ACO
avant (ligne) et après (étoile) l’ajustement
en brisant la symétrie 4. L’expérience
s’ajuste parfaitement sur la théorie, car
les variations de gradients sont faibles, de
l’ordre du pour mille.
de Super-ACO
avant (ligne) et après (étoile) l’ajustement
en brisant la symétrie 4. L’expérience
s’ajuste parfaitement sur la théorie, car
les variations de gradients sont faibles, de
l’ordre du pour mille.
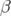 en
brisant la symétrie 4 de Super-ACO. Ces
variations sont faibles.
en
brisant la symétrie 4 de Super-ACO. Ces
variations sont faibles. 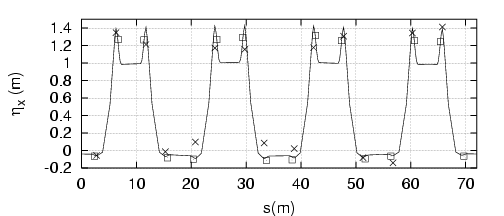


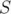 est la force intégrée de l’hexapôle.
est la force intégrée de l’hexapôle.
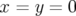 dans l’hexapôle mais
dans l’hexapôle mais  , alors
une composante quadripolaire (et dipolaire) apparaît dans l’expression générale du potentiel
vecteur
, alors
une composante quadripolaire (et dipolaire) apparaît dans l’expression générale du potentiel
vecteur![[ |--------------|
As = − S- (x3 − 3xy2)|− 3x0(x2 − y2)|− 3x2x − x3 (5.16)
3 ---------------------- 0] 0
− 3y2x|− 6y xy − 6y x y − 3y2x
0 -----0---| 0 0 0 0](these2048x.png)

 est le champ intégré d’un quadripôle droit et
est le champ intégré d’un quadripôle droit et  celui d’un quadripôle
tourné (à prendre en compte si l’on considère le couplage).
celui d’un quadripôle
tourné (à prendre en compte si l’on considère le couplage).
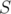 et
et  , on peut également déterminer une mesure
de l’orbite fermée,
, on peut également déterminer une mesure
de l’orbite fermée, 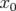 , dans les hexapôles.
, dans les hexapôles.
 mA a été injecté dans 24 paquets avec un faisceau
mA a été injecté dans 24 paquets avec un faisceau 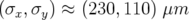 .
Comme les courants alimentant les quadripôles ont changé (cf. Tab.
.
Comme les courants alimentant les quadripôles ont changé (cf. Tab. 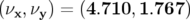 , ce qui est très loin du point de fonctionnement
précédent
, ce qui est très loin du point de fonctionnement
précédent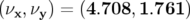
 (cf. chap.
(cf. chap. 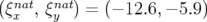
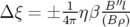 (Edwards et Syphers
(Edwards et Syphers 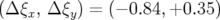
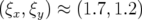
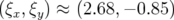
 , et avec les hexapôles
, et avec les hexapôles 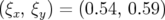 . Ces valeurs sont très différentes de celles
énoncées précédemment.
. Ces valeurs sont très différentes de celles
énoncées précédemment.
 mm, l’écart modèle/expérience est grand,
en moyenne de 50%. Pour le BPM 9, la dispersion est pathologique,
mm, l’écart modèle/expérience est grand,
en moyenne de 50%. Pour le BPM 9, la dispersion est pathologique,  mm, soit le
double de celle des autres BPM
mm, soit le
double de celle des autres BPM mm, l’écart modèle/expérience est
inférieur à 5%.
mm, l’écart modèle/expérience est
inférieur à 5%.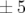 mm) — hexapôles allumés et onduleurs
ouverts — Les écarts relatifs sont plus importants dans les régions non dispersives (BPM 1,
4, 5, 8, 9, 12, 13 et 16 de Super-ACO).
mm) — hexapôles allumés et onduleurs
ouverts — Les écarts relatifs sont plus importants dans les régions non dispersives (BPM 1,
4, 5, 8, 9, 12, 13 et 16 de Super-ACO).
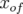 ) dans les quadripôles et les hexapôles
) dans les quadripôles et les hexapôles
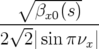
![[ ]
∑ 2
βxi((Kili))
i](these2077x.png)

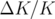 ) des quadripôles
) des quadripôles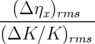

![[ ]
∑ 2
βxi((Kili)ηxi)
i](these2082x.png)

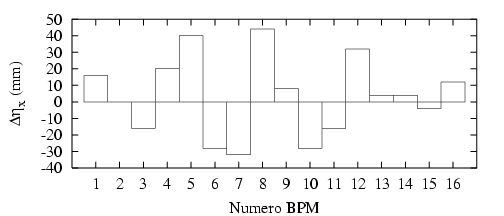
 (H) et
(H) et 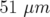 (V) avant
l’ajustement
(V) avant
l’ajustement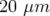 rms (H) et
rms (H) et 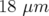 rms (V) avec un
rms (V) avec un 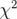 de 1 579. Le point de fonctionnement devient
de 1 579. Le point de fonctionnement devient
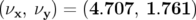 , ce qui est en accord avec les mesures expérimentales
, ce qui est en accord avec les mesures expérimentales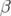 sont donnés par la
figure
sont donnés par la
figure 

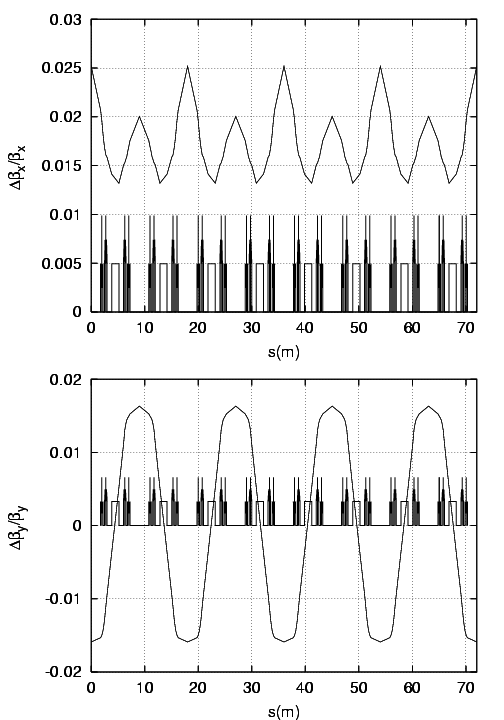
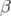 de Super-ACO en symétrie 4 avec hexapôles
expérimentaux.
de Super-ACO en symétrie 4 avec hexapôles
expérimentaux.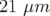 (H) et
(H) et 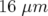 (V) dans chacun des plans avec un
(V) dans chacun des plans avec un  de 926. Les nombres d’ondes finaux valent
de 926. Les nombres d’ondes finaux valent .
.
 . Ces variations sont similaires en termes d’amplitudes à celles trouvées hexapôles
éteints. Les battements des fonctions
. Ces variations sont similaires en termes d’amplitudes à celles trouvées hexapôles
éteints. Les battements des fonctions 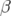 induits sont donnés à titre indicatif par la figure
induits sont donnés à titre indicatif par la figure 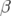 (cf.
Fig.
(cf.
Fig. 
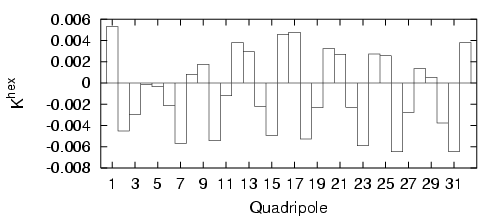

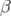 Fig.
Fig. 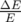 grâce à la
formule
grâce à la
formule 

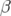 (à gauche) et leurs battements (à droite) en brisant la symétrie 4
de Super-ACO. L’optique est globalement peu perturbée.
(à gauche) et leurs battements (à droite) en brisant la symétrie 4
de Super-ACO. L’optique est globalement peu perturbée.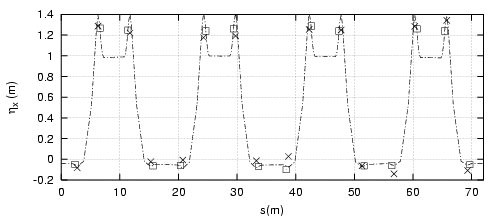
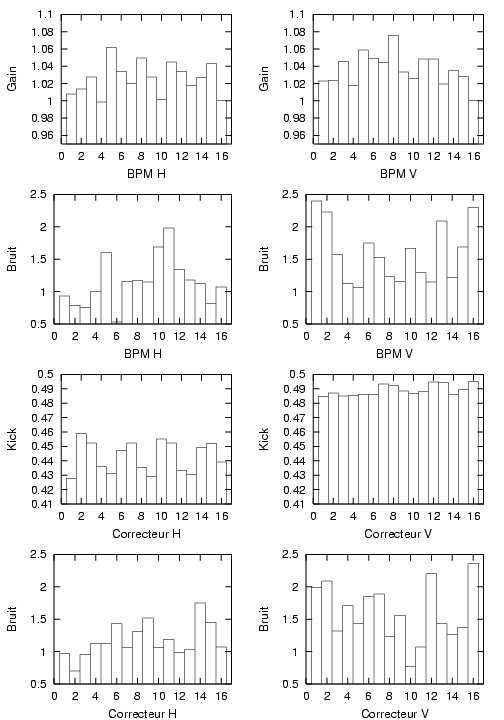
 mA dans 24
paquets — dimensions faisceau
mA dans 24
paquets — dimensions faisceau  —. Les courants quadripolaires et
hexapolaires mesurés sont donnés par le tableau
—. Les courants quadripolaires et
hexapolaires mesurés sont donnés par le tableau 
 , qu’il faut ensuite modifier pour ajouter l’influence de la focalisation des
onduleurs.
, qu’il faut ensuite modifier pour ajouter l’influence de la focalisation des
onduleurs.
 . Ces valeurs calculées en utilisant
les valeurs expérimentales de courant (cf. Tab.
. Ces valeurs calculées en utilisant
les valeurs expérimentales de courant (cf. Tab. 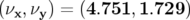 auquel il faudrait encore ajouter l’influence de l’orbite
fermée non nulle dans les hexapôles.
auquel il faudrait encore ajouter l’influence de l’orbite
fermée non nulle dans les hexapôles.
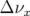

 et
et  ). Le point de fonctionnement déduit des
valeurs expérimentales de courant est alors
). Le point de fonctionnement déduit des
valeurs expérimentales de courant est alors 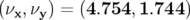 .
.
 en
moyenne.
en
moyenne.
 mm) dans les BPM de Super-ACO —
hexapôles allumés, onduleurs fermés — La fonction dispersion dans les régions non dispersives
a beaucoup changé. Dans les BPM 1, 4 et 16, la fonction dispersion est maintenant positive.
mm) dans les BPM de Super-ACO —
hexapôles allumés, onduleurs fermés — La fonction dispersion dans les régions non dispersives
a beaucoup changé. Dans les BPM 1, 4 et 16, la fonction dispersion est maintenant positive.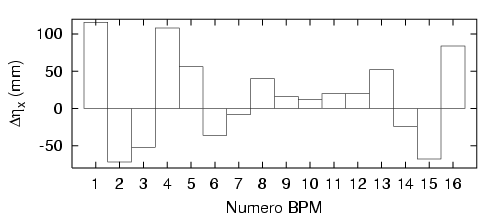

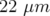 (H) et
(H) et  (V) et un point de fonctionnement
de
(V) et un point de fonctionnement
de  . L’allure des fonctions
. L’allure des fonctions 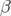 (Fig.
(Fig. 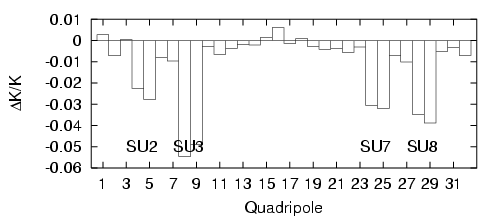

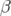 calculées pour une machine théorique avec le logiciel BETA (ligne)
et déduites l’ajustement avec les hexapôles et les onduleurs fermés (étoile). On observe un
bon accord qualitatif avec le modèle (cf. Brunelle, 1992).
calculées pour une machine théorique avec le logiciel BETA (ligne)
et déduites l’ajustement avec les hexapôles et les onduleurs fermés (étoile). On observe un
bon accord qualitatif avec le modèle (cf. Brunelle, 1992).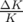 , sont faibles
, sont faibles (Q1),
(Q1),
 (Q2) et
(Q2) et 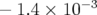 (Q3 et Q4). L’origine principale proviendrait des
courants des alimentations.
(Q3 et Q4). L’origine principale proviendrait des
courants des alimentations.
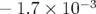 (Q1),
(Q1), 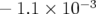 (Q2),
(Q2),  (Q3) et
(Q3) et 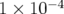 (Q4). Ces
variations s’expliquent par le terme quadripolaire engendré dans les hexapôles lorsque
l’orbite fermée est non nulle.
(Q4). Ces
variations s’expliquent par le terme quadripolaire engendré dans les hexapôles lorsque
l’orbite fermée est non nulle.
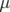 m à environ
m à environ 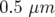 (communication personnelle, C. Steier).
(communication personnelle, C. Steier).
 A, utilisées ici pour enregistrer les matrices-réponse, sont trop faibles pour observer des
termes croisés de la matrice-réponse non nuls compte tenu de la faible résolution des
BPM.
A, utilisées ici pour enregistrer les matrices-réponse, sont trop faibles pour observer des
termes croisés de la matrice-réponse non nuls compte tenu de la faible résolution des
BPM.
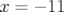 mm et
mm et  mm par pas de 1 mm environ.
mm par pas de 1 mm environ.
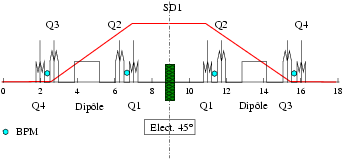
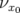
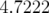
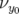

 (h)
(h) 
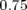





![x[mm ] = 2.8× S[mA −1]− 27.95](these2142x.png)

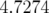
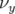


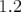

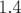
 (A)
(A) 
 (kHz)
(kHz) 
 )
et d’hexapôles (
)
et d’hexapôles ( ) sont utilisées pour
ajuster l’optique de Super-ACO.
) sont utilisées pour
ajuster l’optique de Super-ACO.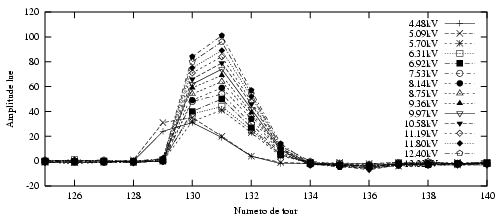
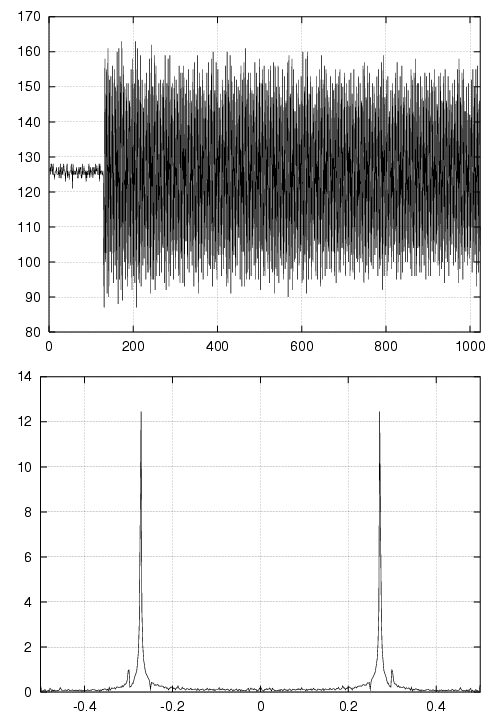

 kV (grande amplitude) et
son spectre de Fourier. La décohérence
est faible et le signal peu bruité.
kV (grande amplitude) et
son spectre de Fourier. La décohérence
est faible et le signal peu bruité. kV (cf. Fig.
kV (cf. Fig.  ) où
) où  est le nombre de tours contenant du signal. Pour une transformée de
Fourier rapide (FFT) traditionnelle
est le nombre de tours contenant du signal. Pour une transformée de
Fourier rapide (FFT) traditionnelle 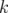 vaut 1 alors que pour l’Analyse en Fréquence
vaut 1 alors que pour l’Analyse en Fréquence 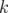 vaut
4.
vaut
4.
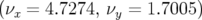 , la variation théorique
des nombres d’ondes est calculée en utilisant le code de calcul MAD version 8
, la variation théorique
des nombres d’ondes est calculée en utilisant le code de calcul MAD version 8
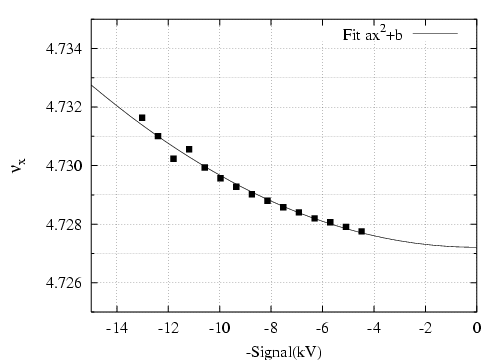
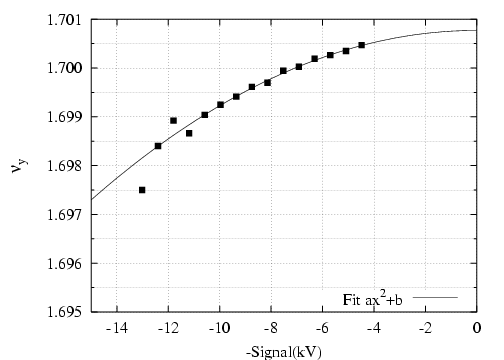
 (à gauche) et
(à gauche) et 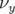 (à
droite) avec l’amplitude horizontale. Dans chacun des cas, la variation du nombre d’ondes est
quadratique avec l’amplitude.
(à
droite) avec l’amplitude horizontale. Dans chacun des cas, la variation du nombre d’ondes est
quadratique avec l’amplitude.

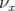 (à gauche) et
(à gauche) et 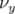 (à droite) avec
l’amplitude horizontale pour différents modèles de Super-ACO et comparaison à l’expérience
(carrés)
(à droite) avec
l’amplitude horizontale pour différents modèles de Super-ACO et comparaison à l’expérience
(carrés)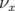 est opposée à celui mesuré.
est opposée à celui mesuré.
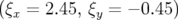 , sont très différentes des chromaticités
mesurées en particulier dans le plan horizontal (défaut de chromaticité naturelle non
modélisé).
, sont très différentes des chromaticités
mesurées en particulier dans le plan horizontal (défaut de chromaticité naturelle non
modélisé).
 . L’écart peut paraître
faible par rapport au cas précédent, cependant les 4 chiffres significatifs ont toute leur
importance du fait de la précision des mesures en salle de contrôle avec l’oscilloscope
et de la précision de l’Analyse en Fréquence.
. L’écart peut paraître
faible par rapport au cas précédent, cependant les 4 chiffres significatifs ont toute leur
importance du fait de la précision des mesures en salle de contrôle avec l’oscilloscope
et de la précision de l’Analyse en Fréquence.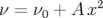
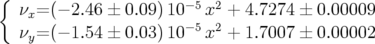

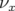 , il semble y avoir vers
, il semble y avoir vers  mm une
perturbation de la dynamique du faisceau — ce n’est pas une erreur sur l’amplitude
du
mm une
perturbation de la dynamique du faisceau — ce n’est pas une erreur sur l’amplitude
du  kV
kV est opposée entre la théorie et l’expérience (cf.
Fig.
est opposée entre la théorie et l’expérience (cf.
Fig. 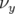 est décroissante avec l’amplitude mais avec une pente beaucoup
plus importante dans le modèle de Super-ACO.
est décroissante avec l’amplitude mais avec une pente beaucoup
plus importante dans le modèle de Super-ACO.
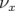 .
.
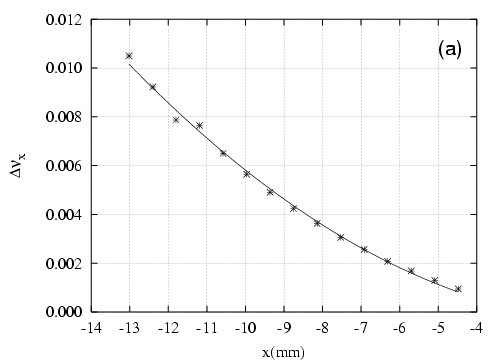
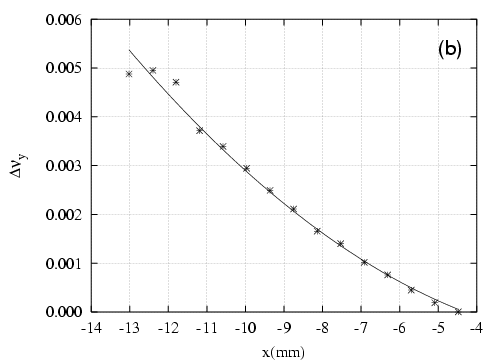
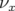 (a) et
(a) et 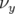 (b) mesurés et prédits
par le modèle de Super-ACO. La loi ajustement (ligne) est dans les deux cas quadratique
avec l’amplitude horizontale.
(b) mesurés et prédits
par le modèle de Super-ACO. La loi ajustement (ligne) est dans les deux cas quadratique
avec l’amplitude horizontale. 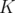 ) des quadripôles et leur
octupôle (
) des quadripôles et leur
octupôle (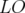 ) lors d’une étude expérimentale de la variation du nombre d’ondes avec
l’énergie de la machine
) lors d’une étude expérimentale de la variation du nombre d’ondes avec
l’énergie de la machine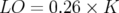
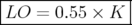
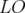 peut
s’écrire
peut
s’écrire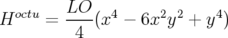
 petit, l’effet est négligeable sur
petit, l’effet est négligeable sur  .
.
 pourrait provenir d’un terme hexapolaire (cf. Fig.
pourrait provenir d’un terme hexapolaire (cf. Fig. 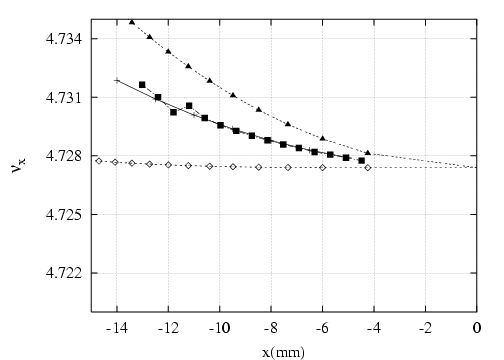

 (à gauche) et
(à gauche) et  (à droite) avec l’amplitude
(à droite) avec l’amplitude
 pour différents modèles de Super-ACO incluant une composante octupolaire. La force des
octupôles est proportionnelle à celle des quadripôles
pour différents modèles de Super-ACO incluant une composante octupolaire. La force des
octupôles est proportionnelle à celle des quadripôles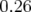 (losanges),
(losanges), 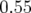 (croix) et
(croix) et  (triangles). Si l’octupôle permet de retrouver le bon
comportement pour
(triangles). Si l’octupôle permet de retrouver le bon
comportement pour 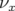 , le désaccord reste grand pour
, le désaccord reste grand pour 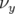 avec la mesure (carrés).
avec la mesure (carrés).
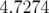
 (A)
(A) 
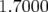
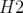 (A)
(A) 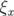
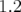
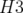 (A)
(A) 

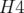 (A)
(A) 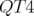 (A)
(A) 
 (A)
(A) 
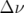 (kHz)
(kHz) 
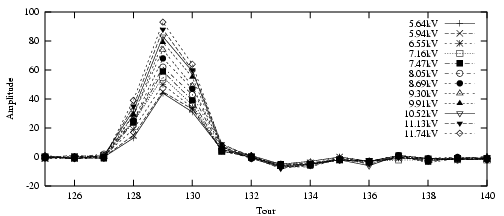
 kV (butée basse) à
kV (butée basse) à  kV (début perte du
faisceau) par pas de 0.5 kV environ.
kV (début perte du
faisceau) par pas de 0.5 kV environ.
![VP 6 ≈ VP 4 + 0.65 [kV ]](these2222x.png)
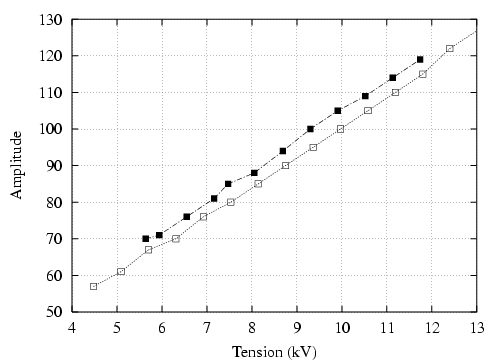
 obtenues après perturbation du
faisceau avec P4 et P6 et après correction des tensions, on observe que les courbes ne
se superposent pas (Fig.
obtenues après perturbation du
faisceau avec P4 et P6 et après correction des tensions, on observe que les courbes ne
se superposent pas (Fig. ![VP 6 ≈ VP4 + 0.65 + 0.95 [kV ]](these2224x.png)




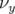



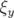
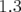
 (A)
(A) 
 (A)
(A) 
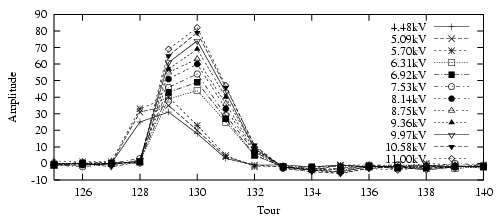
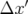 , un phénomène de
décohérence intervient du fait du léger déphasage existant entre chaque particule d’un
paquet. Ce déphasage provient de la dispersion des nombres d’ondes avec l’amplitude,
chaque particule ayant une énergie et une amplitude légèrement différentes des particules
voisines
, un phénomène de
décohérence intervient du fait du léger déphasage existant entre chaque particule d’un
paquet. Ce déphasage provient de la dispersion des nombres d’ondes avec l’amplitude,
chaque particule ayant une énergie et une amplitude légèrement différentes des particules
voisines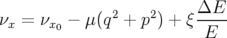
 et
et  où
où 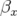 et
et 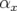 sont les paramètres de Twiss. Si l’on
considère une distribution gaussienne d’écart type
sont les paramètres de Twiss. Si l’on
considère une distribution gaussienne d’écart type 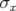 des amplitudes
des amplitudes  et
si l’on néglige le couplage (x-y), l’amortissement, l’excitation quantique et les
interactions entre particules, alors l’évolution du centroïde du faisceau suit la
loi
et
si l’on néglige le couplage (x-y), l’amortissement, l’excitation quantique et les
interactions entre particules, alors l’évolution du centroïde du faisceau suit la
loi
 est le numéro du tour après le
est le numéro du tour après le 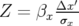 ,
, 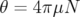 et
et  le facteur chromatique défini par
le facteur chromatique défini par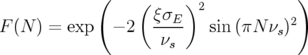
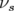 la fréquence synchrotron et
la fréquence synchrotron et  la dispersion en énergie.
la dispersion en énergie.
 , le facteur chromatique
, le facteur chromatique 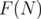 est (
est (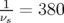 )-tours
périodique).
)-tours
périodique).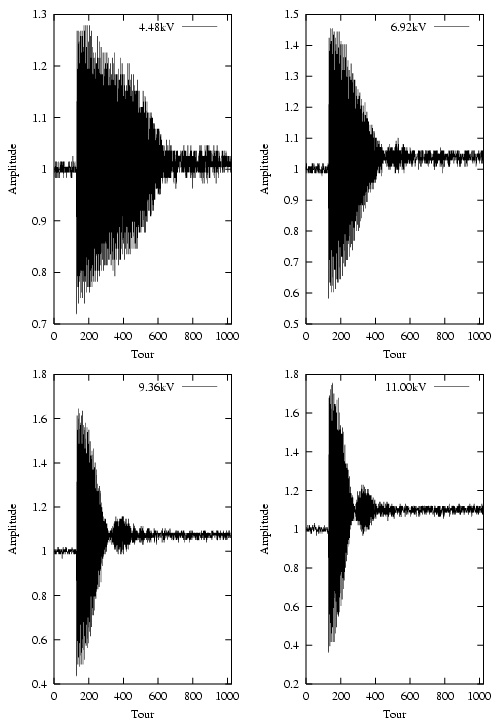
![[− 27, 25] × [− 19, 19]](these2257x.png) mm pour la machine
nominale (
mm pour la machine
nominale (![[− 11, 11] × [− 15, 15]](these2258x.png) mm, soit une réduction d’un facteur deux
horizontalement, ce qui est très proche de l’expérience.
mm, soit une réduction d’un facteur deux
horizontalement, ce qui est très proche de l’expérience. avec l’amplitude horizontale est
calculée pour différents modèles de Super-ACO et comparée avec l’expérience (cf.
Fig.
avec l’amplitude horizontale est
calculée pour différents modèles de Super-ACO et comparée avec l’expérience (cf.
Fig.  avec l’amplitude
avec l’amplitude
 est
est 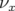 (comparer les courbes avec et
sans octupôles Fig.
(comparer les courbes avec et
sans octupôles Fig. 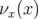 .
.
 )) suffisent
pour retrouver la bonne loi de variation
)) suffisent
pour retrouver la bonne loi de variation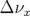 en fonction de l’amplitude (
en fonction de l’amplitude ( ) est très forte
) est très forte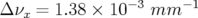 contre
contre  (réglage nominal).
(réglage nominal).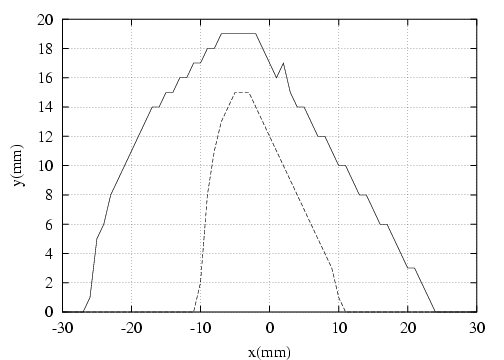

 avec l’amplitude horizontale. Modèles
de Super-ACO avec les chromaticités
expérimentales (triangles), les courants
hexapolaires mesurés (cercles). Seule
l’introduction de composante octupolaire
précédemment proposée (croix) permet de
retrouver la bonne loi de variation (carrés).
avec l’amplitude horizontale. Modèles
de Super-ACO avec les chromaticités
expérimentales (triangles), les courants
hexapolaires mesurés (cercles). Seule
l’introduction de composante octupolaire
précédemment proposée (croix) permet de
retrouver la bonne loi de variation (carrés). en fonction de
en fonction de  sans l’introduction d’une composante forte de
type octupolaire. Dans la présente étude, seuls les octupôles des quadripôles ont été
introduits. Cependant d’autres éléments magnétiques de l’anneau peuvent créer un
octupôle
sans l’introduction d’une composante forte de
type octupolaire. Dans la présente étude, seuls les octupôles des quadripôles ont été
introduits. Cependant d’autres éléments magnétiques de l’anneau peuvent créer un
octupôle , fonction de l’amplitude horizontale. Une tentative
d’introduction d’un hexapôle tourné dans les quadripôles ne permet pas de résoudre ce
problème.
, fonction de l’amplitude horizontale. Une tentative
d’introduction d’un hexapôle tourné dans les quadripôles ne permet pas de résoudre ce
problème.
 mm.
mm.
 . En
approximation
. En
approximation 
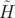 qui a été établie rigoureusement par
Zimmermann
qui a été établie rigoureusement par
Zimmermann

![{ ˜ -1 4 2 2 4
H1 ≈ 12(KQlQ )KQ [x + 6x y + y ]
˜H2 ≈ 152Δ2K2Q (KQlQ )[x4 − y4]](these2279x.png)
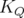 est le gradient du quadripôle et
est le gradient du quadripôle et  sa longueur effective.
sa longueur effective.
 et
et  , le
Hamiltonien moyenné devient en sommant sur tous les quadripôles de la machine (Zimmermann,
2000)
, le
Hamiltonien moyenné devient en sommant sur tous les quadripôles de la machine (Zimmermann,
2000)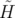


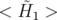 par rapport aux
actions
par rapport aux
actions 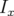 et
et 
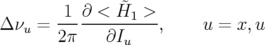
![1 ∑ 2 5 ∑ 2 2 2
Δ νx ≈ --- (KQlQ )KQ [βx,QIx + 2 βx,Q βy,QIy] + --- Δ KQ (KQlQ )βx,QIx
8 π Q 8π Q](these2291x.png)
![1 ∑ 5 ∑
Δ νy ≈ --- (KQlQ )KQ [β2y,QIy + 2 βx,Qβy,QIx] − --- Δ2K2Q (KQlQ )β2y,QIy
8 π Q 8π Q](these2292x.png)
 m,
m, 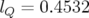 m et les valeurs expérimentales des gradients des quadripôles (cf.
Tab.
m et les valeurs expérimentales des gradients des quadripôles (cf.
Tab. 
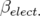 est l’expression de la fonction
est l’expression de la fonction 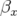 au niveau de l’électrode à 45 degrés.
La contribution des pseudo-octupôles des champs de fuite des quadripôles est tracée sur la
figure
au niveau de l’électrode à 45 degrés.
La contribution des pseudo-octupôles des champs de fuite des quadripôles est tracée sur la
figure 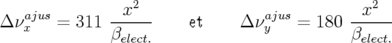
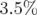 pour
pour 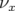 et
et 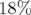 pour
pour 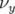 . Ces résultats sont compatibles avec l’incertitude sur les
valeurs expérimentales des fonctions
. Ces résultats sont compatibles avec l’incertitude sur les
valeurs expérimentales des fonctions 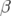 (perturbation de l’optique linéaire et couplage non
modélisés).
(perturbation de l’optique linéaire et couplage non
modélisés).

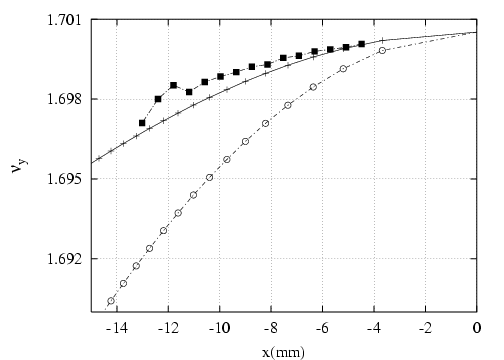
 et
et 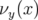 en fonction de l’amplitude
horizontale
en fonction de l’amplitude
horizontale  . Sans pseudo-octupôle, le désaccord (cercles) avec la mesure (carrés) est
important (sens de variation opposé pour
. Sans pseudo-octupôle, le désaccord (cercles) avec la mesure (carrés) est
important (sens de variation opposé pour 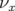 ). L’introduction du pseudo-octupôle (croix)
induit par les champs de fuite des quadripôles de Super-ACO permet de trouver des
glissements des nombres très proches de la mesure dans les deux plans. Glissements des
nombres d’ondes induits
). L’introduction du pseudo-octupôle (croix)
induit par les champs de fuite des quadripôles de Super-ACO permet de trouver des
glissements des nombres très proches de la mesure dans les deux plans. Glissements des
nombres d’ondes induits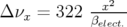 et
et 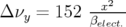 ).
).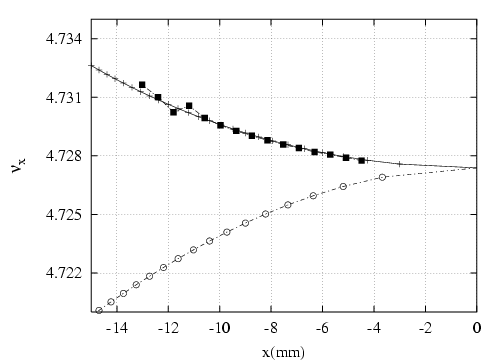

 et
et 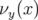 en
fonction de l’amplitude horizontale. Après ajustement des pseudo-octupôles de Super-ACO
(croix) sur la mesure (carrés), les accords sont excellents contrairement au modèle sans
pseudo-octupôle (cercles). Glissements des nombres d’ondes induits
en
fonction de l’amplitude horizontale. Après ajustement des pseudo-octupôles de Super-ACO
(croix) sur la mesure (carrés), les accords sont excellents contrairement au modèle sans
pseudo-octupôle (cercles). Glissements des nombres d’ondes induits et
et
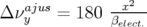 ).
).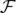 du champ de fuite, pour un quadripôle de gradient
du champ de fuite, pour un quadripôle de gradient  (voir aussi Forest,
1998)
(voir aussi Forest,
1998)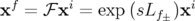
 .
.

 ,
,  et
et  les couples de variables canoniques.
les couples de variables canoniques.
 est le coin supérieur droit de
la carte. Le bord extérieur supérieur (resp. inférieur) correspond à la variation du
nombre d’ondes vertical avec
est le coin supérieur droit de
la carte. Le bord extérieur supérieur (resp. inférieur) correspond à la variation du
nombre d’ondes vertical avec 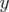 (resp. nombre d’ondes horizontal avec
(resp. nombre d’ondes horizontal avec  ). La carte
en fréquence est repliée sur elle-même. L’ouverture dynamique est réduite car les
chromaticités sont élevées dans les deux plans. La résonance
). La carte
en fréquence est repliée sur elle-même. L’ouverture dynamique est réduite car les
chromaticités sont élevées dans les deux plans. La résonance  est traversée à
grande amplitude,
est traversée à
grande amplitude, 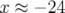 mm.
mm.
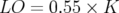 est introduite dans le modèle. Le sens de variation de
est introduite dans le modèle. Le sens de variation de 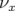 est inversé,
d’autres résonances apparaissent mais globalement leur coefficient d’excitation est assez
faible. Les dimensions de l’ouverture dynamique sont comparables au cas sans octupôle.
est inversé,
d’autres résonances apparaissent mais globalement leur coefficient d’excitation est assez
faible. Les dimensions de l’ouverture dynamique sont comparables au cas sans octupôle.


 , qui expérimentale détériore la
dynamique du faisceau n’est pas excitée.
L’ouverture dynamique (bas) associée
reste grande.
, qui expérimentale détériore la
dynamique du faisceau n’est pas excitée.
L’ouverture dynamique (bas) associée
reste grande.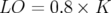 . Dans ce
cas, la dynamique est très fortement détériorée par l’excitation des différentes
résonances.
. Dans ce
cas, la dynamique est très fortement détériorée par l’excitation des différentes
résonances.
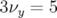 limite l’ouverture dynamique verticale
alors que la résonance
limite l’ouverture dynamique verticale
alors que la résonance  réduit son extension horizontale (voir aussi la
figure
réduit son extension horizontale (voir aussi la
figure 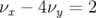 limitait expérimentalement la dynamique du faisceau, alors
l’ouverture dynamique serait réduite à
limitait expérimentalement la dynamique du faisceau, alors
l’ouverture dynamique serait réduite à 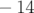 mm horizontalement et
mm horizontalement et  mm
verticalement.
mm
verticalement.
 , l’ouverture dynamique verticale
(bas) est réduite de près d’un facteur
deux (influence de
, l’ouverture dynamique verticale
(bas) est réduite de près d’un facteur
deux (influence de  ). L’ouverture
dynamique horizontale est trois fois plus
petite. Sur les deux figures, la diffusion
est plus importante au voisinage des
résonances.
). L’ouverture
dynamique horizontale est trois fois plus
petite. Sur les deux figures, la diffusion
est plus importante au voisinage des
résonances.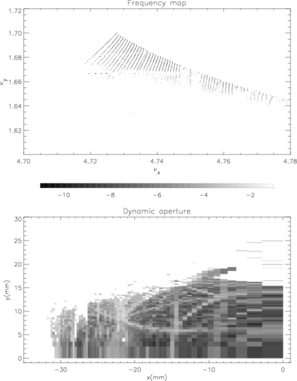
![[− 15, 0] × [0, 6]](these2339x.png) mm, ce qui
serait proche de l’expérience.
mm, ce qui
serait proche de l’expérience.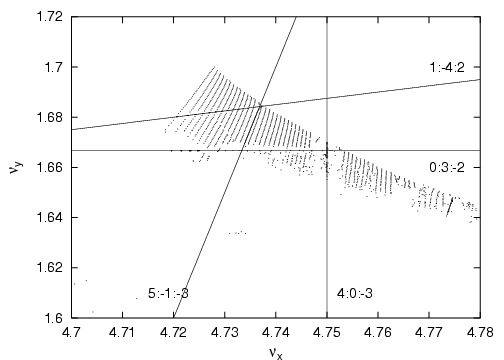
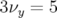 limite la dynamique dans le plan vertical
alors que la résonance
limite la dynamique dans le plan vertical
alors que la résonance  réduit son extension horizontale.
réduit son extension horizontale. et
et 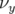 avec l’amplitude horizontale en utilisant l’Analyse en Fréquence
(Laskar, 1990). D’autre part, deux moniteurs de position sont utilisés pour réaliser les premières
mesures d’espaces des phases pour différentes configurations machine
avec l’amplitude horizontale en utilisant l’Analyse en Fréquence
(Laskar, 1990). D’autre part, deux moniteurs de position sont utilisés pour réaliser les premières
mesures d’espaces des phases pour différentes configurations machine mA dans un paquet. A la
suite d’un test avec le perturbateur P4 pour une tension de
mA dans un paquet. A la
suite d’un test avec le perturbateur P4 pour une tension de  kV, une grande partie
du faisceau a été perdue pour une raison inexpliquée. Pour cette expérience, il était
techniquement impossible d’injecter à nouveau du courant, on a donc continué de
travailler avec le courant
kV, une grande partie
du faisceau a été perdue pour une raison inexpliquée. Pour cette expérience, il était
techniquement impossible d’injecter à nouveau du courant, on a donc continué de
travailler avec le courant  mA.
mA.


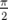 comme initialement désirée mais de
comme initialement désirée mais de 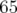 degrés (voir également le
synoptique de l’anneau Fig.
degrés (voir également le
synoptique de l’anneau Fig. 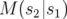 la matrice de transfert entre les deux
BPM, on peut alors écrire (Courant et Snyder, 1958)
la matrice de transfert entre les deux
BPM, on peut alors écrire (Courant et Snyder, 1958)
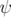 , la différence de phase entre les deux BPM et (
, la différence de phase entre les deux BPM et (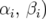 , les paramètres de Twiss en
, les paramètres de Twiss en
 . On en déduit immédiatement la relation
. On en déduit immédiatement la relation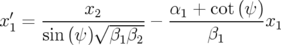
 où
où 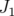 est l’action définie par
est l’action définie par 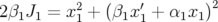 .
.
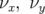
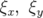
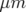 )
) 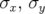



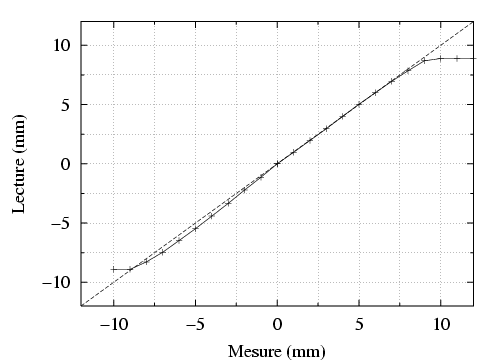

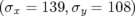
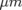

![A [mm ] = 5.224× S [mA −1]− 23.5](these2368x.png)
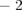



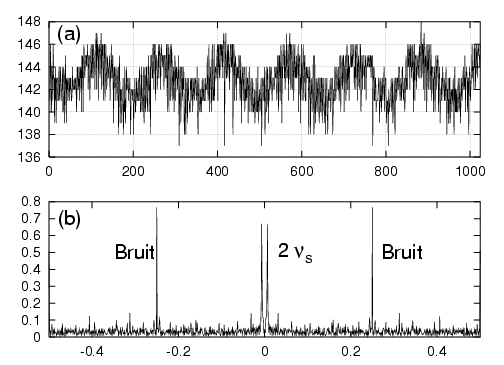
 est observée.
est observée.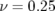


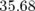


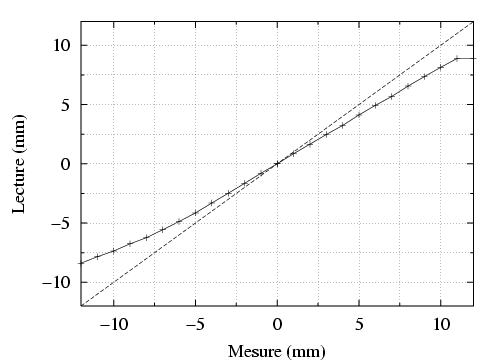
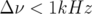 ).
).

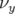
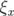
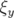

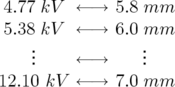

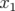 ) en fonction de celui lu sur le deuxième (
) en fonction de celui lu sur le deuxième (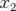 ). Un exemple de
pseudo-ellipse est représenté sur la figure
). Un exemple de
pseudo-ellipse est représenté sur la figure  (cf. Eq.
(cf. Eq. 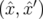 , l’ellipse d’émittance se transforme
en cercle
, l’ellipse d’émittance se transforme
en cercle
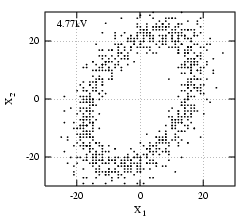
 ). L’épaississement de
l’ellipse est une conséquence de la faible
décohérence du faisceau (sur 1 000
tours, cf. Fig.
). L’épaississement de
l’ellipse est une conséquence de la faible
décohérence du faisceau (sur 1 000
tours, cf. Fig. 
 )
) . L’amplitude
est donnée dans le coin supérieur gauche
des figures.
. L’amplitude
est donnée dans le coin supérieur gauche
des figures.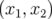 est très déformé pour
est très déformé pour  kV et surtout pour
kV et surtout pour
 kV. Aucun phénomène particulier (résonance, perturbations externes)
n’a pu être mis explicitement en évidence.
kV. Aucun phénomène particulier (résonance, perturbations externes)
n’a pu être mis explicitement en évidence.

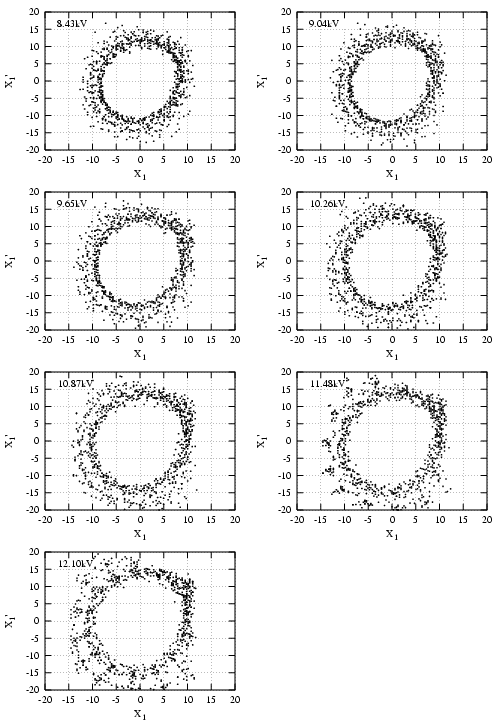
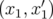 pour de grandes amplitudes
pour de grandes amplitudes peut être extrait du signal puisque le minimum de couplage
est réalisé.
peut être extrait du signal puisque le minimum de couplage
est réalisé.
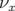 (Eq.
(Eq. 
 , la fonction
, la fonction  au niveau du moniteur de position.
au niveau du moniteur de position.
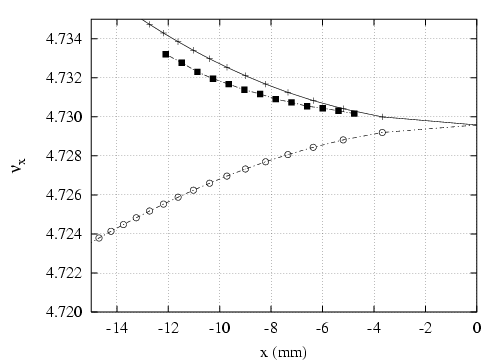
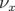 en fonction de l’amplitude horizontale. Comparaison
entre la mesure (carrés) et différentes modélisations de Super-ACO
en fonction de l’amplitude horizontale. Comparaison
entre la mesure (carrés) et différentes modélisations de Super-ACO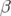 .
.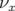
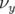

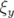
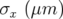
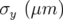
 (kHz)
(kHz) 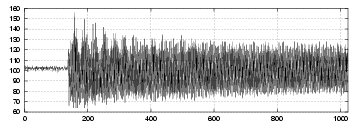
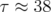 h) et 9.65 kV
(début de perte du faisceau,
h) et 9.65 kV
(début de perte du faisceau, 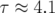 h), soit un total de 9 points de mesure pour les deux
BPM.
h), soit un total de 9 points de mesure pour les deux
BPM.
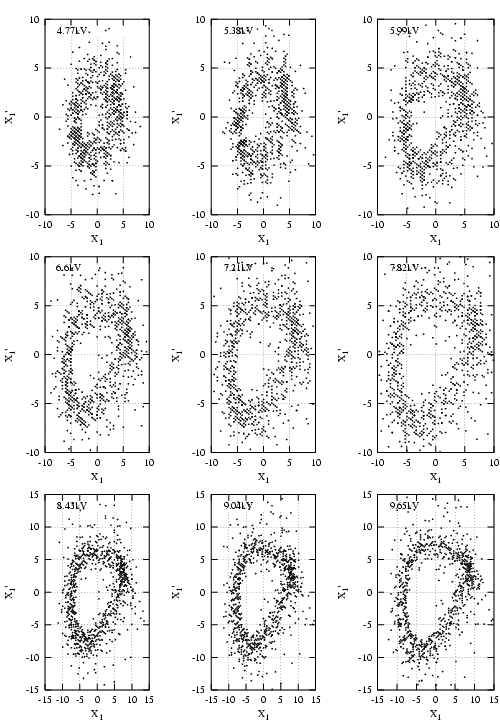
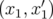 de Super-ACO pour le point de routine
de Super-ACO pour le point de routine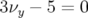 est mise en évidence.
est mise en évidence.

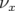 (à gauche) et
(à gauche) et 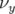 (à droite) en fonction de
l’amplitude horizontale. Comparaison entre la mesure (carrés) et différents modèles de
Super-ACO
(à droite) en fonction de
l’amplitude horizontale. Comparaison entre la mesure (carrés) et différents modèles de
Super-ACO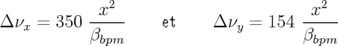
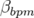 , la fonction
, la fonction 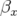 au niveau du moniteur de position. Il est remarquable de
trouver un excellent accord entre la mesure et notre modèle de Super-ACO (cf.
Fig.
au niveau du moniteur de position. Il est remarquable de
trouver un excellent accord entre la mesure et notre modèle de Super-ACO (cf.
Fig. 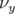 semble provenir d’un terme de couplage non
modélisé.
semble provenir d’un terme de couplage non
modélisé.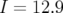 A (durée de vie
A (durée de vie h),
le minimum de couplage est réalisé (QT4 fort), les chromaticités sont élevées dans les
deux plans (cf. Tab.
h),
le minimum de couplage est réalisé (QT4 fort), les chromaticités sont élevées dans les
deux plans (cf. Tab. 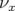
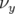
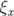
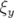
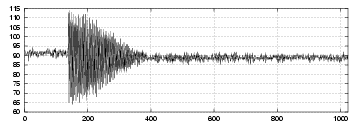
 kV, ne correspondent pas à des
résonances « dangereuses » mais traduisent simplement la rationalité du nombre d’ondes
(
kV, ne correspondent pas à des
résonances « dangereuses » mais traduisent simplement la rationalité du nombre d’ondes
( ).
).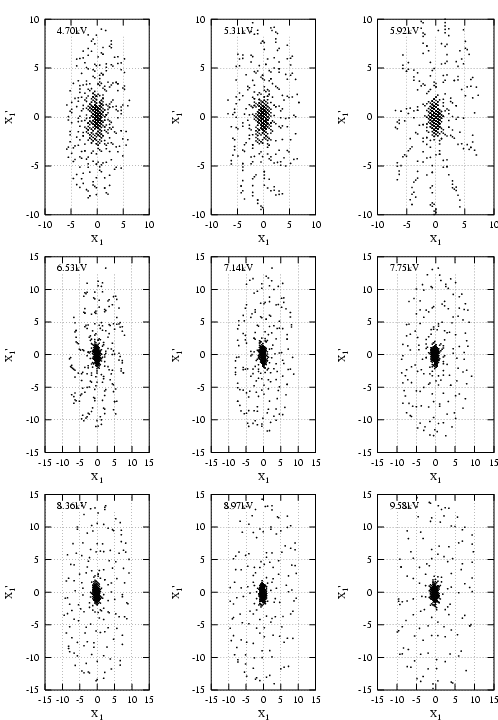
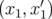 de Super-ACO lorsque les familles
hexapolaires H1 et H2 sont éteintes en réalisant le minimum de couplage
de Super-ACO lorsque les familles
hexapolaires H1 et H2 sont éteintes en réalisant le minimum de couplage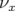 (Eq.
(Eq. 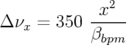
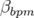 , la fonction
, la fonction  au niveau du moniteur de position. L’accord avec la mesure est
remarquable lorsque les pseudo-octupôles sont pris en compte dans le modèle de
Super-ACO.
au niveau du moniteur de position. L’accord avec la mesure est
remarquable lorsque les pseudo-octupôles sont pris en compte dans le modèle de
Super-ACO.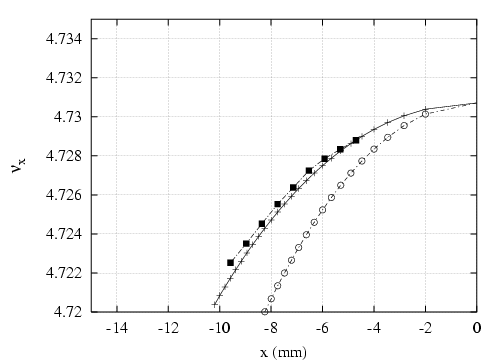
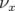 en fonction de l’amplitude horizontale
en fonction de l’amplitude horizontale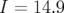 mA (durée de vie
mA (durée de vie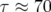 h) ont été
enregistrées, car l’ouverture dynamique est plus petite lorsque le minimum de couplage
n’est pas réalisé (cf. conditions expérimentales Tab.
h) ont été
enregistrées, car l’ouverture dynamique est plus petite lorsque le minimum de couplage
n’est pas réalisé (cf. conditions expérimentales Tab.  h).
h).
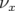

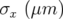
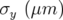
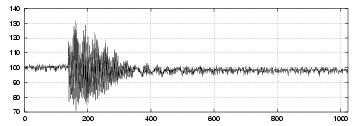
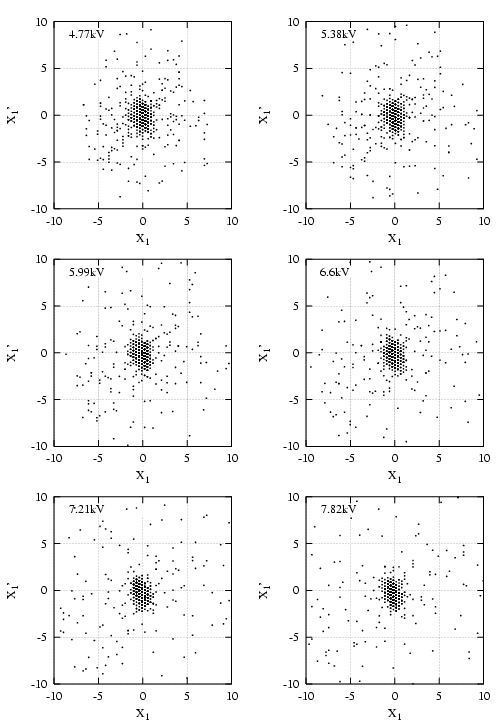
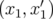 de Super-ACO lorsque les familles H1 et
H2 sont éteintes. La présence de couplage diminue les dimensions de l’ouverture dynamique
et accélère le phénomène de décohérence. L’amplitude initiale du signal est donnée dans le
coin supérieur gauche de chaque figure.
de Super-ACO lorsque les familles H1 et
H2 sont éteintes. La présence de couplage diminue les dimensions de l’ouverture dynamique
et accélère le phénomène de décohérence. L’amplitude initiale du signal est donnée dans le
coin supérieur gauche de chaque figure.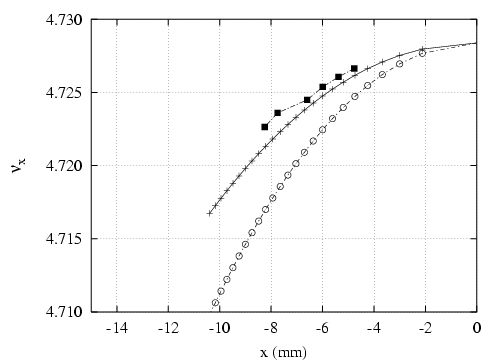
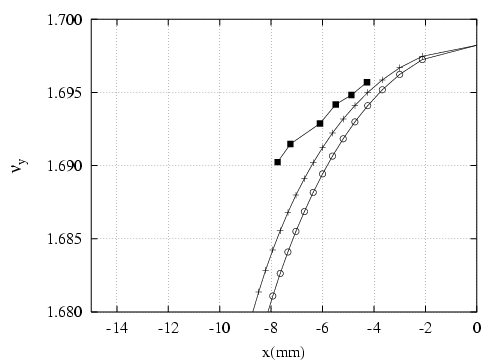
 (à gauche) et
(à gauche) et 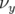 (à droite) en fonction
de l’amplitude horizontale
(à droite) en fonction
de l’amplitude horizontale
 , la fonction
, la fonction 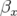 au niveau du moniteur de position.
au niveau du moniteur de position.


 est la fonction optique au point d’observation.
est la fonction optique au point d’observation.
 est liée à celle des quadripôles
est liée à celle des quadripôles 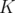 (Barthès
(Barthès 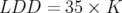
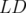 est
proportionnelle à la force hexapolaire
est
proportionnelle à la force hexapolaire  (Brunelle, 1999)
(Brunelle, 1999)