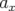 ,
i.e. :
,
i.e. :
Supposons que la fréquence transverse dépende quadratiquement de l’amplitude d’oscillation 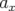 ,
i.e. :
,
i.e. :
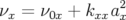 | (4.16) |
Alors le déphase au n-ième tour s’écrit :
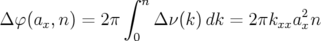 | (4.17) |
L’oscillation bétatron de la particule devient (cf. formule 1.60 p. § avec  ) :
) :
 | (4.18) |
et celle du centroïde de particules distribuées statistiquement selon  :
:
 | (4.19) |
Si 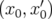 sont les variables de l’espace des phases transverse, alors on sait que l’invariant linéaire
est l’intégrale d’action (cf. définition de l’émittance p. §) :
sont les variables de l’espace des phases transverse, alors on sait que l’invariant linéaire
est l’intégrale d’action (cf. définition de l’émittance p. §) :
![1
Jx0 = ----[x20 + (αxx0 + βxx ′0)2]
2βx](these1691x.png) | (4.20) |
avec 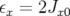 . En supposant des distributions gaussiennes, la fonction densité de probabilité
avant l’impulsion est alors donnée par :
. En supposant des distributions gaussiennes, la fonction densité de probabilité
avant l’impulsion est alors donnée par :
 | (4.21) |
avec  . La distribution dans les variables amplitude-phase
. La distribution dans les variables amplitude-phase 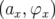 est
alors :
est
alors :
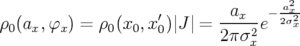 | (4.22) |
avec  et
et
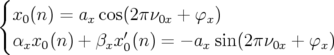 | (4.23) |
La distribution recherchée est celle obtenue immédiatement après que le faisceau a reçu une
impulsion  . On suppose ici que le faisceau est déplacé d’un bloc instantanément au temps
. On suppose ici que le faisceau est déplacé d’un bloc instantanément au temps
 . On déduit alors (cf. Eq. 4.22 et Fig. 4.3) :
. On déduit alors (cf. Eq. 4.22 et Fig. 4.3) :
 | (4.24) |
avec l’amplitude de l’impulsion transverse  .
.
Le mouvement du centroïde du paquet de particules se réécrit alors (Eq. 4.19 et 4.24) :
| < x(n) > | = ∫
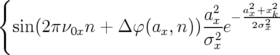 | ||
 dax dax | (4.25) | ||
| l’intégrale sur les cosinus étant nulle, | |||
| < x(n) > | = ∫
 e− e− 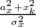 I1
I1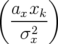 sin(2πν0xn + Δφ(ax,n)) dax sin(2πν0xn + Δφ(ax,n)) dax | (4.26) | |
| avec la fonction de Bessel modifiée I1(x) : | |||
| I1(x) | =  ∫
0π cos(θ)eix cos θ dθ ∫
0π cos(θ)eix cos θ dθ | (4.27) | |
| < x(n) > | = −xkFx sin  | (4.28) | |
| avec | Fx = 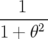 exp exp 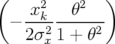 , θ = 4πkxxσx2n , θ = 4πkxxσx2n | ||
 .
.
La décohérence avec l’amplitude d’oscillation introduit le facteur de décohérence 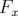 qui
est une gaussienne pour
qui
est une gaussienne pour 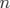 petit et tend asymptotiquement vers une loi en puissance
petit et tend asymptotiquement vers une loi en puissance
 . Le centroïde,
. Le centroïde, 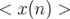 , de phase
, de phase 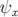 (Eq. 4.28), oscille à la fréquence
instantannée :
(Eq. 4.28), oscille à la fréquence
instantannée :
| νx | =   | (4.29) |
= ν0x + kxx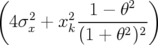 | (4.30) |
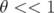 : le faisceau oscille
approximativement à la fréquence
: le faisceau oscille
approximativement à la fréquence 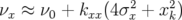 . Le second pour
. Le second pour  , la fréquence
devient
, la fréquence
devient  , ce qui correspond au cas où le faisceau a entièrement « décohéré » (son
amplitude d’oscillation moyenne est nulle).
, ce qui correspond au cas où le faisceau a entièrement « décohéré » (son
amplitude d’oscillation moyenne est nulle).