 et des ouvertures dynamiques à
et des ouvertures dynamiques à 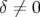 presque nulles
conduisent une durée de vie du faisceau très faible (cf. dynamique longitudinale, limitation par
l’acceptance en énergie).
presque nulles
conduisent une durée de vie du faisceau très faible (cf. dynamique longitudinale, limitation par
l’acceptance en énergie).
Les machines de rayonnement synchrotron de troisième génération sont construites sur des optiques à forte focalisation afin d’atteindre de performances toujours plus extrêmes : les petites émittances créées permettent d’obtenir les hautes brillances recherchées. Cependant, de telles contraintes impliquent l’utilisation de champs magnétiques de forte intensité qui eux-mêmes vont exciter de nombreuses résonances et risquent ainsi de détériorer la dynamique globale du faisceau et de conduire à une faible ouverture dynamique et une faible acceptance en énergie. Il en résulte une injection lente et une faible durée de vie. Ces effets indésirables doivent être minimisés tout en concervant une haute brillance. Une des tâches principales du physicien des accélérateurs se résume d’abord à déterminer la meilleure optique possible de la machine, ensuite à définir une modélisation aussi proche que possible de la réalité et enfin, à développer des méthodes susceptibles d’améliorer la stabilité de la dynamique du faisceau.
L’optique des sources de lumière de troisième génération est construite généralement sur une maille dite Chasman-Green ou double bend achromat1 (Super-ACO, SOLEIL, ESRF) ou une maille triple bend achromat2 (ALS). Les faibles émittances y sont créées en minimisant les fonctions bétatrons dans les dipôles, ce qui se traduit par l’utilisation de forts champs dans les quadripôles adjacents. Nous avons vu (chap. 1, p. § sqq.) que ces derniers créent alors une grande chromaticité naturelle dans les deux plans qui est compensée par l’introduction de lentilles hexapolaires : deux familles, dites chromatiques, suffisent. Cependant très souvent, d’autres familles d’hexapôles sont également introduites dans la maille pour minimiser les largeurs des résonances. La principale difficulté est de déterminer l’emplacement optimum de ces hexapôles autour de l’anneau ainsi que leur force. Seuls des choix judicieux permettent de réduire les nonlinéarités.
La dynamique des particules individuelles est une des causes principales de la limitation des performances des sources de lumière. Si les orbites sont instables aux grandes amplitudes, alors les électrons diffusés à ces grandes amplitudes lors de collisions avec les atomes du gaz résiduel ou avec d’autres électrons (effet Touschek) vont être perdus par le faisceau. Il en sera de même pour les particules injectées à grande amplitude (optimisation de l’injection).
A la connaissance de l’auteur, seule l’ouverture dynamique des particules d’énergie nominale est
optimisée3
pour réduire l’influence des phénomènes nonlinéaires ; ces derniers peuvent conduire à la divergence
rapide des trajectoires des particules et à une chute drastique des performances globales de la
machine. Les ouvertures dynamiques des particules off momentum ne sont que rarement optimisées
pour les sources de lumière. Ce point peut conduire à des situations paradoxales : par exemple, une
très grande ouverture dynamique à  et des ouvertures dynamiques à
et des ouvertures dynamiques à 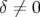 presque nulles
conduisent une durée de vie du faisceau très faible (cf. dynamique longitudinale, limitation par
l’acceptance en énergie).
presque nulles
conduisent une durée de vie du faisceau très faible (cf. dynamique longitudinale, limitation par
l’acceptance en énergie).
Cependant à l’heure actuelle, il n’existe pas de méthode analytique systématique pour arriver à
ces fins (même pour l’optimisation on momentum, i.e. pour  ), la difficulté provenant de la
détermination des amplitudes des résonances. Généralement, le schéma retenu consiste à utiliser
des familles d’hexapôles pour minimiser l’influence des résonances d’ordre trois, considérées comme
les plus néfastes pour la dynamique. Il est souvent admis, mais à tort, que seules les résonances
d’ordre faible sont à corriger (voir le rapport du CERN de Guignard, 1978 où l’auteur reformule
une théorie des perturbations du premier ordre). Pourtant les hexapôles excitent les
résonances de tout ordre (comme nous l’avons observé pour l’application d’Hénon, p. §
sqq.). La méthode utilisée pour Super-ACO ou SOLEIL repose sur le travail réalisé par
Audy (1989) : les coefficients analytiques des amplitudes des résonances d’ordre 3 sont
calculés puis minimisés par ajustement (c’est une méthode de perturbation du premier
ordre).
), la difficulté provenant de la
détermination des amplitudes des résonances. Généralement, le schéma retenu consiste à utiliser
des familles d’hexapôles pour minimiser l’influence des résonances d’ordre trois, considérées comme
les plus néfastes pour la dynamique. Il est souvent admis, mais à tort, que seules les résonances
d’ordre faible sont à corriger (voir le rapport du CERN de Guignard, 1978 où l’auteur reformule
une théorie des perturbations du premier ordre). Pourtant les hexapôles excitent les
résonances de tout ordre (comme nous l’avons observé pour l’application d’Hénon, p. §
sqq.). La méthode utilisée pour Super-ACO ou SOLEIL repose sur le travail réalisé par
Audy (1989) : les coefficients analytiques des amplitudes des résonances d’ordre 3 sont
calculés puis minimisés par ajustement (c’est une méthode de perturbation du premier
ordre).
Deux questions viennent tout de suite à l’esprit : (1) est-il possible de prédire quelles résonances sont susceptibles d’être excitées sur la machine réelle ? (2) est-il possible d’établir une méthode pour identifier facilement les résonances et d’estimer leurs amplitudes ?
Un début de réponse peut être apporté par l’utilisation de la théorie des perturbations en calculant des formes normales. Elles ont été introduites en Physique des Accélérateurs principalement par Dragt et Forest (Université de Maryland) et sont très utilisées au CERN. Bien que donnant de bons résultats (voir par exemple Todesco, Gemmi et Giovannozzi, 1997 et une application au LHC par Papaphilippou et Schmidt, 1998), cette méthode est assez lourde à mettre en œuvre. Des corrections locales sont possibles mais cette méthode dépend fortement de la modélisation et ne permet pas d’effectuer simplement des comparaisons directes entre le modèle et la machine en fonctionnement.
L’Analyse en Fréquence est au contraire une méthode numérique qui permet de manière assez intuitive et pratique d’identifier des résonances et d’estimer leur amplitude. Nous allons l’appliquer à quatre sources de lumière : le Projet SOLEIL, l’ESRF, Super-ACO et l’ALS. Pour chacune de ces machines, nous calculerons des cartes en fréquence ainsi que les ouvertures dynamiques associées. Les résultats seront présentés soit pour une modélisation purement théorique, soit pour une machine en fonctionnement (cf. résultats expérimentaux, chapitres sur l’ALS et Super-ACO). Nous montrerons la grande sensibilité de la dynamique aux réglages magnétiques.
Par soucis de clarification, je tiens à dire que ces deux approches sont complémentaires. La théorie des perturbations a été introduite à une époque où les gros ordinateurs n’existaient pas. Elle a permis et permet encore d’obtenir des formules analytiques relativement simples utilisées pour améliorer le réglage d’un accélérateur et comprendre sa dynamique (e.g. glissement des nombres d’ondes avec l’amplitude, déformation de l’espace des phases, largeur des résonances). Cette méthode ne fonctionne plus si le système est trop perturbé. Elle est moins précise que les intégrateurs numériques pour déterminer les équations du mouvement. La seconde approche repose sur les outils numériques. Elle permet une détermination précise de la trajectoire d’une particule (intégrateurs, codes de tracking) aussi bien pour un régime faiblement que fortement perturbé. Son inconvénient majeur est d’être une « boîte noire » qui fournit peu d’informations pour une compréhension théorique du mouvement nonlinéaire (approche qualitative).
Pour l’ensemble des résultats qui vont être présentés, nous ne prenons en compte que la
dynamique transverse en négligeant le mouvement longitudinal. Ce choix est justifié dans la mesure
où le nombre d’ondes longitudinal 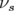 est très faible devant les nombres d’ondes transverses : par
exemple pour SOLEIL, la fréquence longitudinale est
est très faible devant les nombres d’ondes transverses : par
exemple pour SOLEIL, la fréquence longitudinale est  et les nombres d’ondes sont
et les nombres d’ondes sont
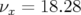 et
et 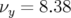 .
.
La majorité des cartes en noir et blanc du corps du mémoire sont reproduites en couleur en annexe B.