4.3 La décohérence ab ovo

Le modèle que nous allons présenter est inspiré de la publication de Lee (1992), donnée lors du Workshop on Nonlinear Problems In Accelerator Physics de Berlin. Ce modèle est bidimensionnel, les particules sont supposées distribuées transversalement et longitudinalement suivant une loi de Gauss et la variation des nombres d’ondes est supposée linéaire en l’écart en énergie et quadratique en l’amplitude, i.e.  :

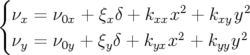(4.1)

D’autres papiers ont été également très instructifs, voir par exemple Meller et al. (1987) et Ian (1990), ainsi que pour une formulation en variables actions-angles Shi et Ohnuma (1993).

Pour la présente formulation de la décohérence, les phénomènes suivants sont négligés :

• le couplage transverse x-y,
• le couplage synchro-bétatron,
• les phénomènes d’amortissement, d’excitation quantique, de mutuelle interaction des particules.