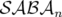 et
et 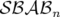 ont été programmés pour
ont été programmés pour  et
et 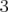 . Des
intégrateurs d’ordre plus élévé pourront sans difficulté être introduits par la suite. Pour
les comparaisons internes, l’intégrateur d’ordre 4 de Forest et Ruth a également été
programmé.
. Des
intégrateurs d’ordre plus élévé pourront sans difficulté être introduits par la suite. Pour
les comparaisons internes, l’intégrateur d’ordre 4 de Forest et Ruth a également été
programmé.
Un code d’intégration numérique a été écrit en langage FORTRAN90. Ce code prend en
compte l’ensemble des modèles d’éléments magnétiques précédemment présentés. Ce
programme est écrit de manière modulaire afin de pouvoir traiter les petites et grandes
machines ; il est possible d’introduire de nouveaux éléments magnétiques (e.g. les dispositifs
d’insertion) ; le code est dédié et optimisé pour le tracking. Les intégrateurs avec ou sans
correcteur de type 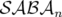 et
et 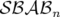 ont été programmés pour
ont été programmés pour  et
et  . Des
intégrateurs d’ordre plus élévé pourront sans difficulté être introduits par la suite. Pour
les comparaisons internes, l’intégrateur d’ordre 4 de Forest et Ruth a également été
programmé.
. Des
intégrateurs d’ordre plus élévé pourront sans difficulté être introduits par la suite. Pour
les comparaisons internes, l’intégrateur d’ordre 4 de Forest et Ruth a également été
programmé.
Différents types de comparaisons ont été effectués, en particulier avec les codes DESPOT et MAD respectivement sur une maille de l’ALS (grande machine) et de Super-ACO (petite machine). Les calculs ont été réalisés en double précision sur une station DIGITAL PWS 433 AU (EV56 à 433 MHz).
Précision : Nous avons vérifié la précision de l’intégration pour chaque élément magnétique modélisé. Le Hamiltonien est une intégrale première du mouvement. Nous présentons quelques résultats pour le dipôle combiné dans l’approximation des grandes machines. Son Hamiltonien est rappelé :
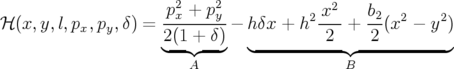 |
avec comme courbure 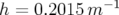 , gradient quadripolaire
, gradient quadripolaire 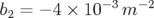 et longueur
et longueur
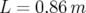 . Le dipôle est ainsi focalisant dans les deux plans.
. Le dipôle est ainsi focalisant dans les deux plans.
Tout d’abord, il est nécessaire de remarquer que le Hamiltonien s’apparente à celui de deux
oscillateurs. Les parties 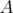 et
et 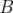 sont comparables i.e. le petit paramètre
sont comparables i.e. le petit paramètre  est voisin de
l’unité. Donc pour cet élément, il sera inutile de vouloir utiliser un intégrateur d’ordre
supérieur à 4 puisque la nouvelle classe d’intégrateurs n’a d’intérêt qui si
est voisin de
l’unité. Donc pour cet élément, il sera inutile de vouloir utiliser un intégrateur d’ordre
supérieur à 4 puisque la nouvelle classe d’intégrateurs n’a d’intérêt qui si  est un petit
paramètre.
est un petit
paramètre.
Les erreurs sur l’énergie du dipôle combiné sont calculées sur un temps d’intégration de 1 000
passages à travers l’aimant (Fig. 2.4). Pour l’intégration exacte (cf. annexe A.2.4, page §), l’erreur
est aléatoire avec une dérive numérique linéaire du nombre d’itérations comme attendu (la
précision machine est 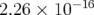 ).
).
Les trois schémas symplectiques choisis sont le schéma de Ruth et le schéma 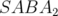 et
et
 avec correcteur. Le dipôle de longueur
avec correcteur. Le dipôle de longueur 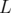 est intégré en trois étapes d’intégration
(
est intégré en trois étapes d’intégration
( ). La meilleure des méthodes est l’intégrateur
). La meilleure des méthodes est l’intégrateur 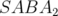 qui est plus d’un ordre de grandeur
plus précis que le schéma de Ruth (Fig. 2.4).
qui est plus d’un ordre de grandeur
plus précis que le schéma de Ruth (Fig. 2.4).
|
Une étude systématique de la précision des méthodes a également été réalisée. Les intégrateurs
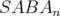 et
et 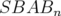 avec correcteur sont comparés à coût constant (i.e. à nombre égal
d’évaluations) avec le schéma de Ruth. L’erreur relative des intégrateurs symplectiques est
présentée pour
avec correcteur sont comparés à coût constant (i.e. à nombre égal
d’évaluations) avec le schéma de Ruth. L’erreur relative des intégrateurs symplectiques est
présentée pour  en fonction du nombre d’étapes d’intégration pour un aimant de longueur
en fonction du nombre d’étapes d’intégration pour un aimant de longueur
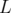 (Fig. 2.5). En échelle logarithmique, la pente des droites est 4, ce qui correspond à l’ordre des
méthodes utilisées. La méthode
(Fig. 2.5). En échelle logarithmique, la pente des droites est 4, ce qui correspond à l’ordre des
méthodes utilisées. La méthode 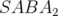 avec correcteur est plus précise que le schéma de Ruth
d’un ordre de grandeur.
avec correcteur est plus précise que le schéma de Ruth
d’un ordre de grandeur.
Ce résultat va pouvoir être utilisé pour diminuer, à précision constante, le temps d’intégration des élément magnétique, soit de réduire le temps de tracking. Généralement, une à deux étapes d’intégration sont gagnées par comparaison avec l’intégrateur de Forest et Ruth.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Un autre point remarquable de cette nouvelle classe d’intégrateurs est sa faible dérive en phase à
nombre égal d’itérations. En comparant la solution numérique obtenue par le schéma symplectique
par rapport à la solution exacte, on note que le déphasage introduit par la méthode 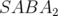 est
très faible par rapport à l’intégrateur de Ruth et Forest (voir Fig. 2.6 pour le dipôle
combiné et Fig. 2.7 pour une maille complète de l’ALS). Par exemple, le tableau 2.3
donne le nombre
est
très faible par rapport à l’intégrateur de Ruth et Forest (voir Fig. 2.6 pour le dipôle
combiné et Fig. 2.7 pour une maille complète de l’ALS). Par exemple, le tableau 2.3
donne le nombre  de tours de l’ALS pour obtenir un déphasage
de tours de l’ALS pour obtenir un déphasage  de
de  pour
différentes valeurs du nombre d’étapes
pour
différentes valeurs du nombre d’étapes 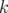 d’intégration des dipôles et des quadripôles de
l’anneau12.
Une loi d’échelle entre le temps d’intégration
d’intégration des dipôles et des quadripôles de
l’anneau12.
Une loi d’échelle entre le temps d’intégration 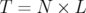 et le nombre d’étapes
et le nombre d’étapes 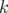 d’intégration
peut être établie. Si
d’intégration
peut être établie. Si 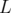 est la longueur de l’élément intégré
est la longueur de l’élément intégré  fois, et si
fois, et si 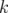 est le nombre
d’étapes pour intégrer l’aimant. Alors le pas de l’intégrateur pour chaque étape est
est le nombre
d’étapes pour intégrer l’aimant. Alors le pas de l’intégrateur pour chaque étape est 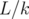 et on
établit :
et on
établit :
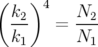 |
où 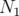 ,
, 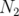 correspondent au nombre de fois qu’il faut intégrer l’aimant de longueur
correspondent au nombre de fois qu’il faut intégrer l’aimant de longueur 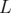 ,
respectivement en
,
respectivement en 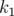 et
et 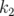 étapes, pour obtenir un déphasage
étapes, pour obtenir un déphasage  entre le schéma symplectique (
entre le schéma symplectique (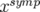 ) et exact (
) et exact (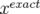 ). En effet, en se souvenant que
la méthode est d’ordre 4 et en ne gardant que les termes de plus bas degré, on peut
écrire :
). En effet, en se souvenant que
la méthode est d’ordre 4 et en ne gardant que les termes de plus bas degré, on peut
écrire :
 |
Notons que le déphasage n’est pas une grandeur fondamentale pour déterminer si un intégrateur numérique est meilleur qu’un autre. Nous avons vu précédemment qu’un intégrateur symplectique peut être vu comme un modèle d’un élément magnétique. Ainsi pour retrouver les bons nombres d’ondes, il suffirait d’ajuster les conditions initiales.
|
|
Jusqu’à présent, l’analyse de la précision des méthodes symplectiques n’a pas été
réalisée. Cependant, une remarque concernant la taille des pas d’intégration peut
être faite. Pour cela, décrivons succinctement le schéma d’intégration numérique
d’un élément de longueur  avec l’intégrateur
avec l’intégrateur  dont l’expression est
rappelée13 :
dont l’expression est
rappelée13 :
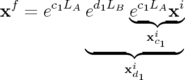 | (2.60) |
avec 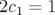 et
et  . Dans ce cas l’intégration est réalisée en deux pas suivant
. Dans ce cas l’intégration est réalisée en deux pas suivant 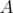 et un pas
suivant
et un pas
suivant 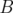 . Si l’intégration est réalisée en
. Si l’intégration est réalisée en 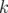 étapes, le schéma d’intégration 2.60 est composé
étapes, le schéma d’intégration 2.60 est composé 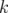 fois avec un pas
fois avec un pas 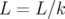 .
.
|
|
Ce processus est illustré pour les intégrateurs 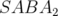 et de Forest et Ruth (schéma 2.8 pour
et de Forest et Ruth (schéma 2.8 pour
 ). Pour l’intégrateur
). Pour l’intégrateur 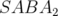 les pas, tous positifs, sont petits, plus fins sur les bords de
l’élément et plus grands en son centre (cf. condition 2.20). L’intégrateur de Forest et Ruth est
caractérisé par la présence de grandes valeurs de pas. Pour intégrer
les pas, tous positifs, sont petits, plus fins sur les bords de
l’élément et plus grands en son centre (cf. condition 2.20). L’intégrateur de Forest et Ruth est
caractérisé par la présence de grandes valeurs de pas. Pour intégrer 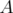 , on fait deux pas positifs
, on fait deux pas positifs
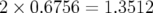 et deux pas négatifs
et deux pas négatifs 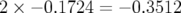 ; pour intégrer
; pour intégrer 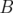 , deux pas
positifs
, deux pas
positifs 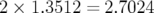 et un grand pas négatif
et un grand pas négatif 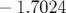 .
.
La valeur des pas d’intégration a probablement une incidence sur la taille du reste des méthodes symplectiques et donc sur leur précision et phase. Des études plus complètes pourront être entreprises pour préciser ces phénomènes.
Conclusion :
Dans les approximations réalisées, il est nécessaire de trouver un compromis entre la précision et
le temps de calcul. L’utilisateur peut selon les besoins modifier la précision de calcul en jouant sur le
nombre d’étapes d’intégration d’un élément de longueur 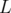 . La nouvelle classe d’intégrateurs
utilisée permet de d’obtenir un intégrateur plus efficace que le schéma classique de Forest et Ruth à
précision de calcul égale.
. La nouvelle classe d’intégrateurs
utilisée permet de d’obtenir un intégrateur plus efficace que le schéma classique de Forest et Ruth à
précision de calcul égale.