Vers un modèle plus réaliste (I)

3.4.3 Vers un modèle plus réaliste (I)

Une maille plus réaliste de l’ALS peut être modélisée en prenant en compte les erreurs de gradients déduites de l’analyse de la matrice-réponse²⁰ non couplée (Robin, Safranek et Decking, 1998 et 1999) en utilisant le programme LOCO (Safranek, 1997). Les matrices-réponse de l’anneau sont mesurées chaque semaine pour déterminer si l’optique de la machine a changé ou non de manière signiﬁcative. Les défauts mesurés sur les forces quadripolaires correspondent en moyenne à des variations de 0.36% rms des valeurs nominales pour les quadripôles défocalisants et 0.2% rms pour les quadripôles focalisant ; ces variations sont loin d’être négligeables et vont induire de profondes modiﬁcations de la dynamique.

Les nouvelles carte en fréquence et ouverture dynamique sont données par la ﬁgure 3.49 (voir aussi la carte en couleur B.13) : la dynamique globale est complètement modiﬁée, la 12-périodicité brisée, donc la condition de résonance est beaucoup moins sévère. En particulier la résonance entière $νx = 8$ est excitée par les défauts quadripolaires comme la théorie le prévoit (voir par exemple chap. II in Accelerator Physics, Lee, 1998) et toutes les orbites dans son voisinage et à plus grandes amplitudes sont instables (quelques centaines de tours).

Les nouvelles dimensions de l’ouverture dynamique sont maintenant $[0, 12] × [0, 8]$ mm. L’ouverture dynamique horizontale est maintenant plus petite que l’ouverture physique (cf. Tab. 3.15). En eﬀet dans le plan horizontal, elle est limitée par la résonance de couplage $νx − 2 νy + 2 = 0$ . Expérimentalement, en utilisant un scraper²¹ horizontal ou en déplaçant le faisceau, nous retrouvons une ouverture dynamique similaire (Decking et Robin, 1999).

pict

FIG. 3.49:

Carte en fréquence (a) et ouverture dynamique (b) de l’ALS : maille avec défauts quadripolaires mesurés pour un surface de section en $s=0$ ( $β = 11.3 m x$ et $β = 4.0m y$ ). La 12-périodicité de l’anneau est brisée, l’extension spatiale de la carte en fréquence est réduite d’un facteur 2 dans le plan vertical.

pict

FIG. 3.50:

Carte en fréquence (a) et ouverture dynamique (b) de l’ALS ( $βx=11.3 m$ et $βy = 4.0 m$ ) : inﬂuence d’un couplage eﬀectif de 1% ajusté à partir des quadripôles tournés. La diﬀusion est globalement plus élevée. Seule la région voisine du point de fonctionnement reste régulière.

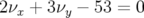L’extension de la carte en fréquence est réduite verticalement d’un facteur deux. Les résonances d’ordre 5 sont excitées : $4νx + νy − 65 = 0$ , $3νx + 2νy − 59 = 0$ et $2νx + 3νy − 53 = 0$ , ce sont des résonances non permises par la 12-périodicité (cf. Fig. 3.51).

De manière générale, la zone de stabilité est réduite au voisinage du point de fonctionnement. Toutes les particules ayant un indice de diﬀusion inférieur à moins six seront sans doute perdues si l’on intègre les trajectoires plus longtemps.

[next] [prev] [prev-tail] [front] [up]