1.2 Paquets circulant dans un anneau de stockage à une vitesse proche de la lumière
 , autour de l’orbite de référence. Au sein de chaque paquet, les
particules oscillent en longitude et en énergie (dynamique longitudinale) —
inspiré de Sands, 1970 —
, autour de l’orbite de référence. Au sein de chaque paquet, les
particules oscillent en longitude et en énergie (dynamique longitudinale) —
inspiré de Sands, 1970 — 1.3 Repère de Serret-Frenet
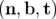 . Définition
des coordonnées curvilignes
. Définition
des coordonnées curvilignes 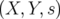 utilisées pour écrire les équations du
mouvement d’une particule autour de la trajectoire de référence.
utilisées pour écrire les équations du
mouvement d’une particule autour de la trajectoire de référence. 1.4 Plan d’antisymétrie pour un dipôle, un quadripôle et un hexapôle droits.
1.5 Ellipse invariante dans l’espace des phases (
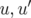 ). L’aire de l’ellipse est
). L’aire de l’ellipse est  ;
;
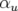 ,
, 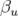 et
et 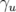 sont les fonctions de Twiss.
sont les fonctions de Twiss. 1.6 Diagramme des résonances jusqu’à l’ordre 8 avec (a) et sans (b) 12-périodicité (exemple de l’ALS). La symétrie interne d’un accélérateur est utilisée pour augmenter la stabilité globale de la dynamique. Le point de fonctionnement d’une machine est choisi dans une région du diagramme où il y a peu de résonances.
2.1 Schéma succinct d’un bloc rectiligne (a) et courbe (b) de longueur
 . Les axes
de coordonnées sont portés par les faces d’entrée et de sortie des blocs
— inspiré de Forest et Hirata (1992) —
. Les axes
de coordonnées sont portés par les faces d’entrée et de sortie des blocs
— inspiré de Forest et Hirata (1992) —2.2 Schéma d’un aimant secteur (a) et d’un aimant à faces parallèles (b). Les angles des coins d’entrée et de sortie sont ici égaux :
 .
.2.3 Schéma du profil magnétique longitudinal d’un aimant de longueur
 . En approximation hard-edge,
le champ magnétique est constant dans l’élément et nul à l’extérieur. En
réalité, le champ magnétique décroît jusqu’à une valeur nulle de part et
d’autre sur une longueur
. En approximation hard-edge,
le champ magnétique est constant dans l’élément et nul à l’extérieur. En
réalité, le champ magnétique décroît jusqu’à une valeur nulle de part et
d’autre sur une longueur 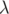 : on parle de champ de fuite.
: on parle de champ de fuite.2.4 Comparaison à coût constant des intégrateurs
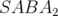 ,
, 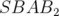 avec correcteur et
Ruth, pour un dipôle combiné. Erreur sur l’énergie
avec correcteur et
Ruth, pour un dipôle combiné. Erreur sur l’énergie 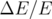 en fonction
du nombre
en fonction
du nombre  de passages dans l’aimant. Pour les schémas symplectiques
l’erreur est bornée et périodique.
de passages dans l’aimant. Pour les schémas symplectiques
l’erreur est bornée et périodique.2.5 Erreur relative sur l’énergie en échelle logarithmique en fonction de la taille du pas d’intégration
 . Les
intégrateurs
. Les
intégrateurs 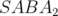 ,
, 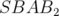 avec correcteur sont plus précis que
l’intégrateur de Forest et Ruth respectivement d’un ordre et d’un demi
ordre de grandeur.
avec correcteur sont plus précis que
l’intégrateur de Forest et Ruth respectivement d’un ordre et d’un demi
ordre de grandeur.2.6 Déphasage
 des solutions du dipôle combiné
introduit par les schémas
des solutions du dipôle combiné
introduit par les schémas 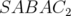 et de Ruth par rapport à la solution
« exacte ». Le déphasage est inférieur de deux ordres de grandeur pour
la nouvelle classe d’intégrateur.
et de Ruth par rapport à la solution
« exacte ». Le déphasage est inférieur de deux ordres de grandeur pour
la nouvelle classe d’intégrateur.2.7 Déphasage introduit par les schémas symplectiques pour l’intégration sur
 tours de l’ALS. Les quadripôles
et dipôles sont intégrés en
tours de l’ALS. Les quadripôles
et dipôles sont intégrés en  étapes. Dès 5 441 tours, le schéma de
Ruth introduit un déphasage complet (remarquer la différence d’échelle
verticale pour les deux méthodes).
étapes. Dès 5 441 tours, le schéma de
Ruth introduit un déphasage complet (remarquer la différence d’échelle
verticale pour les deux méthodes).2.8 Schéma pour l’intégration des parties
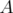 et
et  d’un Hamiltonien avec (a) l’intégrateur de Forest et
Ruth et (b) l’intégrateur
d’un Hamiltonien avec (a) l’intégrateur de Forest et
Ruth et (b) l’intégrateur  .
.2.9 Espace des phases d’un système à deux degrés de liberté en coordonnées actions-angles
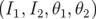 . Les
orbites (
. Les
orbites (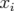 ) sont confinées sur des tores de dimension 2.
) sont confinées sur des tores de dimension 2.2.10 Section de Poincaré (a) : à chaque tour de l’accélérateur, la trajectoire discrète de la particule est enregistrée dans le plan
 . (b) Espace des phases
. (b) Espace des phases
 au temps (i).
au temps (i). 2.11 Diffusion pour un système à deux degrés de liberté (a), e.g. l’application d’Hénon (cf. infra) : la diffusion est confinée par les trajectoires régulières qui sont des points dans l’espace des fréquences. Pour trois degrés de liberté (b), e.g. la dynamique transverse d’un accélérateur, la diffusion n’est plus confinée par les trajectoires régulières ; la diffusion est cependant faible en leur voisinage (Laskar, 1994)
2.12 Espace des phases
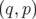 du pendule rigide
(a) et courbes en fréquence
du pendule rigide
(a) et courbes en fréquence 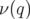 . Au voisinage du point hyperbolique
(b), la courbe en fréquence présente une singularité logarithmique. Au
voisinage du point elliptique (c), la courbe en fréquence est nulle (plateau).
Après échantillonnage en moment
. Au voisinage du point hyperbolique
(b), la courbe en fréquence présente une singularité logarithmique. Au
voisinage du point elliptique (c), la courbe en fréquence est nulle (plateau).
Après échantillonnage en moment 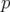 , les projections (d et e) des courbes en
fréquences sont identiques pour le régime de circulation.
, les projections (d et e) des courbes en
fréquences sont identiques pour le régime de circulation. 2.13 Perturbation d’un système : destruction d’un tore rationnel de fréquence
 en
quatre points fixes elliptiques et quatre points fixes hyperboliques. Les
tores irrationels sont faiblement déformés. Au voisinage de chaque point
elliptique, le raisonnement peut être réappliqué.
en
quatre points fixes elliptiques et quatre points fixes hyperboliques. Les
tores irrationels sont faiblement déformés. Au voisinage de chaque point
elliptique, le raisonnement peut être réappliqué. 2.14 Portraits de phase
 et courbes en fréquence associées
et courbes en fréquence associées 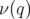 pour
pour  de l’application
d’Hénon. La fréquence linéaire
de l’application
d’Hénon. La fréquence linéaire 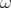 a été choisie dans chacun des cas
pour mettre en évidence des résonances d’ordre 4 (a,
a été choisie dans chacun des cas
pour mettre en évidence des résonances d’ordre 4 (a, 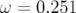 ), 5 (b,
), 5 (b,
 ), 6 (c,
), 6 (c,  ) et 7 (d,
) et 7 (d, 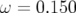 ). Des résonances d’ordre
plus élevé apparaissent et limitent l’ouverture dynamique.
). Des résonances d’ordre
plus élevé apparaissent et limitent l’ouverture dynamique. 2.15 Ouverture dynamique (
 ) associée à l’application d’Hénon en fonction de la
fréquence linéaire
) associée à l’application d’Hénon en fonction de la
fréquence linéaire 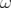 normalisée par
normalisée par 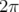 . L’ouverture dynamique est
limitée par la résonance entière pour
. L’ouverture dynamique est
limitée par la résonance entière pour  . Au-delà, elle est
contrainte par des résonances d’ordre plus élevé. L’ouverture dynamique
est nulle pour
. Au-delà, elle est
contrainte par des résonances d’ordre plus élevé. L’ouverture dynamique
est nulle pour  et
et 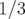 ; elle est infinie en
; elle est infinie en  .
. 2.16 Section de Poincaré en
 pour un accélérateur de particules et trajectoire de
phase
pour un accélérateur de particules et trajectoire de
phase 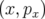 enregistrée aux temps discrets
enregistrée aux temps discrets  .
. 2.17 Carte en fréquence (a) et ouverture dynamique (b) calculées pour une maille parfaite de l’ALS pour la surface de section
 (
(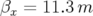 et
et  ). Trois
types de zones sont observés : zones régulières (A), les résonances (B) et
les régions chaotiques (C). Une résonance est révélée différemment suivant
qu’elle est traversée au voisinage des régions hyperboliques ou elliptiques.
La diffusion des orbites est codée suivant une échelle logarithmique en
niveaux de gris. L’échantillonnage dans l’ouverture dynamique suit une
loi en racine carrée de la distance à l’origine.
). Trois
types de zones sont observés : zones régulières (A), les résonances (B) et
les régions chaotiques (C). Une résonance est révélée différemment suivant
qu’elle est traversée au voisinage des régions hyperboliques ou elliptiques.
La diffusion des orbites est codée suivant une échelle logarithmique en
niveaux de gris. L’échantillonnage dans l’ouverture dynamique suit une
loi en racine carrée de la distance à l’origine.3.1 Fonctions optiques pour une maille de SOLEIL.
3.2 (a) : Glissement des nombres d’ondes avec l’amplitude. Dans chaque cas, une des positions
 ou
ou  est fixée à
est fixée à
 (quasi-absence de couplage entre les deux plans). Cette optique a
initialement été conçue pour contraindre les courbes en fréquence entre les
résonances d’ordre 7 et 9. (b) : Carte en fréquence de l’optique numéro 1 de
SOLEIL avec identification des principales résonances. La dynamique est
perturbée par la résonance 5:2:-2 et à grande amplitude par la résonance
entière d’ordre 9 (région chaotique). Le point de fonctionnement est à
l’intersection des deux droites en pointillés.
(quasi-absence de couplage entre les deux plans). Cette optique a
initialement été conçue pour contraindre les courbes en fréquence entre les
résonances d’ordre 7 et 9. (b) : Carte en fréquence de l’optique numéro 1 de
SOLEIL avec identification des principales résonances. La dynamique est
perturbée par la résonance 5:2:-2 et à grande amplitude par la résonance
entière d’ordre 9 (région chaotique). Le point de fonctionnement est à
l’intersection des deux droites en pointillés. 3.3 (a) Carte en fréquence et (b) ouverture dynamique de l’optique faible émittance numéro 1 de SOLEIL calculées pour une surface de Poincaré en
 (
( m
et
m
et  m). L’ouverture dynamique est grande. Elle est marquée par
les résonances ; en particulier, la protubérance observée vers
m). L’ouverture dynamique est grande. Elle est marquée par
les résonances ; en particulier, la protubérance observée vers  mm
correspond à la résonance d’ordre 9. La diffusion est codée en niveaux de
gris. Elle est plus importante au voisinage des résonances et sur le bord de
l’ouverture dynamique (grande amplitude).
mm
correspond à la résonance d’ordre 9. La diffusion est codée en niveaux de
gris. Elle est plus importante au voisinage des résonances et sur le bord de
l’ouverture dynamique (grande amplitude).3.4 Influence du déplacement d’un hexapôle sur la carte en fréquence de l’optique numéro 1 de SOLEIL : la résonance d’ordre 7, 5:2:-2 est fortement excitée. Toutes les orbites ayant des nombres d’ondes au-delà sont maintenant instables. L’extension de la carte en fréquence est réduite de plus d’un facteur deux selon
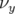 .
.
3.5 Diffusion à long terme (grossissement de la carte 3.2-b de SOLEIL). (O1) Orbite régulière. (O2) Diffusion transverse rapide et longitudinale lente par rapport à la résonance
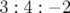 . (O3) Diffusion rapide dans
une région chaotique : la particule est perdue après 5 380 tours de machine.
. (O3) Diffusion rapide dans
une région chaotique : la particule est perdue après 5 380 tours de machine.
3.6 Optique 1 modifiée de SOLEIL (
 m et
m et 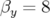 m) : Carte en
fréquence avec les principales résonances (surface de Poincaré en
m) : Carte en
fréquence avec les principales résonances (surface de Poincaré en  ).
La carte en fréquence est repliée sur elle-même, e.g. au voisinage du point
de fonctionnement qui est à l’intersection des deux droites en pointillés.
).
La carte en fréquence est repliée sur elle-même, e.g. au voisinage du point
de fonctionnement qui est à l’intersection des deux droites en pointillés.
3.7 Variation des nombres d’ondes avec l’amplitude à faible couplage (
 ) pour l’optique 1 modifiée de SOLEIL. La résonance d’ordre 7 est
traversée a faible et grande amplitude. Par contre la résonance d’ordre 9
n’est plus atteinte (comparer avec les courbes 3.2-a).
) pour l’optique 1 modifiée de SOLEIL. La résonance d’ordre 7 est
traversée a faible et grande amplitude. Par contre la résonance d’ordre 9
n’est plus atteinte (comparer avec les courbes 3.2-a).3.8 Variation des nombres d’ondes avec l’amplitude à faible couplage (
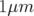 ) pour l’optique 2
de SOLEIL. Les hexapôles ont été réglés de manière à ne plus traverser
les résonances d’ordre 7 et 9 qui marquaient la dynamique (comparer avec
les courbes 3.2-a).
) pour l’optique 2
de SOLEIL. Les hexapôles ont été réglés de manière à ne plus traverser
les résonances d’ordre 7 et 9 qui marquaient la dynamique (comparer avec
les courbes 3.2-a).3.9 Carte en fréquence (a) et ouverture dynamique (b) pour une surface de Poincaré en
 (
( m et
m et  m) pour
l’optique 1 modifiée de SOLEIL. L’ouverture dynamique est presque aussi
grande que pour la première optique ; la carte en fréquence est repliée sur
elle-même : sa lecture en est rendue plus difficile. Son extension spatiale est
réduite, moins de résonances sont rencontrées. La diffusion des orbites est
globalement plus faible.
m) pour
l’optique 1 modifiée de SOLEIL. L’ouverture dynamique est presque aussi
grande que pour la première optique ; la carte en fréquence est repliée sur
elle-même : sa lecture en est rendue plus difficile. Son extension spatiale est
réduite, moins de résonances sont rencontrées. La diffusion des orbites est
globalement plus faible. 3.10 Carte en fréquence (a) et ouverture dynamique (b) pour une surface de Poincaré en
 (
( m et
m et 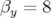 m)
l’optique 2 de SOLEIL. Les glissements des nombres d’onde sont faibles,
ce qui se traduit par une faible extension de la carte en fréquence, une
faible diffusion et une grande ouverture dynamique. La carte en fréquence
est repliée sur elle-même par deux fois.
m)
l’optique 2 de SOLEIL. Les glissements des nombres d’onde sont faibles,
ce qui se traduit par une faible extension de la carte en fréquence, une
faible diffusion et une grande ouverture dynamique. La carte en fréquence
est repliée sur elle-même par deux fois. 3.11 Synoptique de Super-ACO. L’anneau possède une symétrie 4. Ses 32 quadripôles sont répartis en 4 familles. Chacun des 8 dipôles courbe la trajectoire d’une particule d’un angle moyen de 45˚.
3.12 Une des 4 mailles de Super-ACO à symétrie centrale. La structure suit une schéma de Chasman-Green (deux dipôles). Les familles de quadripôles
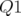 et
et  servent à ajuster les nombres d’ondes,
la fonction dispersion est réglée avec les deux autres familles.
servent à ajuster les nombres d’ondes,
la fonction dispersion est réglée avec les deux autres familles. 3.13 Schéma d’une coupe d’un demi-quadripôle de Super-ACO. L’hexapôle est créé par un mauvais dipôle. Deux bobines de corrections peuvent être utilisées pour la correction dipolaire ou quadripolaire (extrait de Barthès et al., 1990).
3.14 Schéma équivalent d’un quadripôle combiné de Super-ACO. L’hexapôle (H) et le décapôle (LD) sont modélisés par des lentilles minces.
3.15 Un exemple de non symplecticité : une particule test de conditions initiales
 cm et
cm et  est intégrée sur 5 000 tours au second
l’ordre avec le code BETA. Normalement, la trajectoire des phases devrait
être une ellipse passant par la condition initiale (le système est dans ce
cas à un degré de liberté). On observe au contraire une trajectoire spirale
vers le centre de l’espace des phases (x,x’) comme en présence d’un terme
d’amortissement. Les points de la trajectoire ne sont pas reliés par soucis de
lisibilité.
est intégrée sur 5 000 tours au second
l’ordre avec le code BETA. Normalement, la trajectoire des phases devrait
être une ellipse passant par la condition initiale (le système est dans ce
cas à un degré de liberté). On observe au contraire une trajectoire spirale
vers le centre de l’espace des phases (x,x’) comme en présence d’un terme
d’amortissement. Les points de la trajectoire ne sont pas reliés par soucis de
lisibilité.3.16 Comparaison des glissements des nombres d’ondes calculés à l’ordre scaling en mode QXZ, XZ de BETA et avec l’intégrateur LIE4 de MAD sur 1 000 tours de Super-ACO. Les calculs des décapôles ne sont pas corrects à grandes amplitudes (
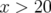 mm) avec le code BETA (cf.
faible rayon de courbure de l’anneau).
mm) avec le code BETA (cf.
faible rayon de courbure de l’anneau). 3.17 Fonctions optiques pour une des quatre super-périodes de Super-ACO : machine idéale.
3.18 Maille idéale de Super-ACO : Glissement des nombres d’ondes avec l’amplitude obtenus avec le programme MAD (LIE4) sur 1 000 tours (à couplage faible
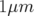 ).
).
3.19 Ouverture dynamique de Super-ACO (
 m et
m et  m)
obtenue avec les codes BETA (contour, calcul rapide) et MAD sur 1 000
tours (calcul long).
m)
obtenue avec les codes BETA (contour, calcul rapide) et MAD sur 1 000
tours (calcul long). 3.20 Cartes en fréquence (c et a) tracées pour le premier (
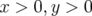 ) et second (
) et second ( ) quadrant de l’ouverture
dynamique (d et b). Super-ACO est modélisé comme machine idéale
(
) quadrant de l’ouverture
dynamique (d et b). Super-ACO est modélisé comme machine idéale
( m et
m et 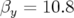 m). Le point de fonctionnement est le coin
supérieur droit de la carte. La dynamique est principalement dominée par la
résonance d’ordre 3
m). Le point de fonctionnement est le coin
supérieur droit de la carte. La dynamique est principalement dominée par la
résonance d’ordre 3 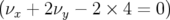 qui donne la limite verticale
de l’ouverture dynamique (
qui donne la limite verticale
de l’ouverture dynamique ( mm). Toute la partie
mm). Toute la partie 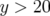 mm
sur l’ouverture dynamique (d) correspond à l’île de cette résonance. La
diffusion est codée en niveaux de gris suivant une échelle logarithmique.
mm
sur l’ouverture dynamique (d) correspond à l’île de cette résonance. La
diffusion est codée en niveaux de gris suivant une échelle logarithmique.
3.21 Résonances principales (traits pleins) et point de fonctionnement (traits pointillés) pour Super-ACO modélisée comme machine idéale. La carte en repliée sur elle-même pour
 .
. 3.22 (a) Ecart entre le gradient mesuré et nominal de chaque quadripôle normalisé par le gradient nominal du quadripôle 3 (mesures magnétiques aléatoires de l’ordre du pour mille, Barthès et al., 1990). (b) Carte en fréquence de Super-ACO et résonances (traits pleins) identifiées lorsque les défauts de gradients sont modélisés. Le point de fonctionnement est le coin supérieur droit de la carte.
3.23 Carte en fréquence (a) et ouverture dynamique (b) calculées en incluant dans le modèle les mesures magnétiques des quadripôles droits de Super-ACO (
 m et
m et  m). La diffusion est globalement
plus élevée, les largeurs de résonances plus grandes. L’influence des défauts
magnétiques reste faible (mêmes dimensions de l’ouverture dynamique).
m). La diffusion est globalement
plus élevée, les largeurs de résonances plus grandes. L’influence des défauts
magnétiques reste faible (mêmes dimensions de l’ouverture dynamique).
3.24 Fonctions optiques sur une super-période de Super-ACO : réglage nominal.
3.25 Glissement des nombres d’ondes
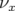 et
et 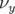 avec l’amplitude
: calculs effectué avec l’intégrateur LIE4 de MAD et l’ordre scaling de
BETA sur 1 000 tours de l’anneau Super-ACO. A grande amplitude
(
avec l’amplitude
: calculs effectué avec l’intégrateur LIE4 de MAD et l’ordre scaling de
BETA sur 1 000 tours de l’anneau Super-ACO. A grande amplitude
( mm), le désaccord est flagrant : les lentilles décapolaires ne
sont plus correctement prises en compte par le code BETA (la résonance
mm), le désaccord est flagrant : les lentilles décapolaires ne
sont plus correctement prises en compte par le code BETA (la résonance
 n’est donc pas observée).
n’est donc pas observée). 3.26 Super-ACO deuxième quadrant (
 ) : carte en fréquence et ouverture dynamique pour le point
de fonctionnement nominal (
) : carte en fréquence et ouverture dynamique pour le point
de fonctionnement nominal ( m et
m et  m). La carte en
fréquence est très compacte : peu de résonances sont rencontrées. Il est difficile
de comprendre avec cette modélisation les observations expérimentales.
m). La carte en
fréquence est très compacte : peu de résonances sont rencontrées. Il est difficile
de comprendre avec cette modélisation les observations expérimentales.
3.27 Fonctions optiques de l’ESRF
3.28 Ouverture dynamique de l’ESRF : premier jeu hexapolaire, section de Poincaré en
 (
(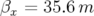 et
et
 ). Bien que très grande, elle est irrégulière, fortement marquée
par les résonances et dissymétrique.
). Bien que très grande, elle est irrégulière, fortement marquée
par les résonances et dissymétrique. 3.29 Carte en fréquence (a et c) et ouverture dynamique (b et d) de l’ESRF: premier jeu hexapolaire pour une surface de section en
 (
(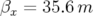 et
et  ). La dynamique
est dominée par la résonance de couplage 3:-2:0 et la résonance entière
). La dynamique
est dominée par la résonance de couplage 3:-2:0 et la résonance entière
 . Les zones elliptiques et hyperboliques associées sont nettement
identifiables sur l’ouverture dynamique (b).
. Les zones elliptiques et hyperboliques associées sont nettement
identifiables sur l’ouverture dynamique (b). 3.30 Carte en fréquence de l’ESRF séparée en deux parties (a et c) pour faciliter la lecture: premier jeu hexapolaire, pour
 , (
, (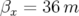 et
et  ). L’ouverture
physique représentée par un rectangle dans l’ouverture dynamique (b et d).
). L’ouverture
physique représentée par un rectangle dans l’ouverture dynamique (b et d).
3.31 Principales résonances pour la dynamique du premier jeu hexapolaire de l’ESRF. Le point de fonctionnement est à l’intersection des droites en pointillés. La dynamique est marquée par la résonance de couplage 3:-2:0 et la résonance entière
 .
. 3.32 (a): Variation de la partie fractionnaire des nombres d’ondes avec l’énergie
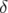 pour le premier réglage de l’ESRF.
(b) : Excursion du point de fonctionnement dans l’espace des fréquence
pour
pour le premier réglage de l’ESRF.
(b) : Excursion du point de fonctionnement dans l’espace des fréquence
pour 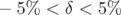 . Les résonances systématiques sont tracées
jusqu’à l’ordre 9.
. Les résonances systématiques sont tracées
jusqu’à l’ordre 9. 3.33 Dynamique off momentum pour le premier jeu hexapolaire de l’ESRF (Colonne 1 :
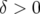 , colonne 2 :
, colonne 2 : 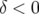 ). Les cartes
en fréquence sont profondément modifiées entre
). Les cartes
en fréquence sont profondément modifiées entre  et
et 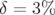 (extension spatiale, repliement, résonances). Le point de fonctionnement
se rapproche de la résonance entière qui détruit la dynamique pour
(extension spatiale, repliement, résonances). Le point de fonctionnement
se rapproche de la résonance entière qui détruit la dynamique pour 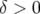 ,
alors que pour
,
alors que pour 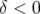 la dynamique est de plus en plus stable. L’ouverture
physique est représentée par un rectangle en traits pleins.
la dynamique est de plus en plus stable. L’ouverture
physique est représentée par un rectangle en traits pleins.3.34 Durée de vie Touschek (
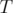 ) en fonction de la tension RF (
) en fonction de la tension RF (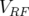 ) pour le premier
réglage de l’ESRF en mode multipaquets (a) et faible nombre de paquets
(b). Une saturation de la durée de vie est observée pour les calculs en mode
nonlinéaire (cercles) par rapport au calcul linéaire (carrés).
) pour le premier
réglage de l’ESRF en mode multipaquets (a) et faible nombre de paquets
(b). Une saturation de la durée de vie est observée pour les calculs en mode
nonlinéaire (cercles) par rapport au calcul linéaire (carrés). 3.35 Variation de l’ouverture dynamique horizontale (
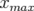 ) de l’ESRF avec l’énergie
(
) de l’ESRF avec l’énergie
(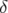 ) pour le premier réglage hexapolaire. Les dimensions (carrés) sont
données par rapport à l’orbite fermée. En supposant que la résonance
entière
) pour le premier réglage hexapolaire. Les dimensions (carrés) sont
données par rapport à l’orbite fermée. En supposant que la résonance
entière 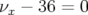 limite l’ouverture dynamique, les dimensions (cercles)
sont restreintes pour
limite l’ouverture dynamique, les dimensions (cercles)
sont restreintes pour 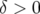 . Ces dimensions sont prises en compte pour
le calcul de la durée de vie Touschek en mode nonlinéaire.
. Ces dimensions sont prises en compte pour
le calcul de la durée de vie Touschek en mode nonlinéaire. 3.36 Ouverture dynamique : second jeu hexapolaire de l’ESRF pour
 , (
, ( et
et  ). Elle est toujours très dissymétrique mais plus régulière
que pour le premier jeu hexapolaire.
). Elle est toujours très dissymétrique mais plus régulière
que pour le premier jeu hexapolaire.3.37 Carte en fréquence et ouverture dynamique calculées pour le second réglage hexapolaire de l’ESRF pour une surface de section à
 (
( et
et  ). La dynamique est
dominée par la résonance d’ordre 5,
). La dynamique est
dominée par la résonance d’ordre 5,  . La diffusion
(niveaux de gris) est assez faible avec une grande ouverture dynamique.
. La diffusion
(niveaux de gris) est assez faible avec une grande ouverture dynamique.
3.38 Carte en fréquence de l’ESRF séparée en deux parties (a et c) pour faciliter la lecture: second réglage hexapolaire, pour
 , (
, (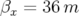 et
et 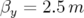 ). L’ouverture physique représentée par un rectangle dans
l’ouverture dynamique associée (b et d).
). L’ouverture physique représentée par un rectangle dans
l’ouverture dynamique associée (b et d).3.39 Principales résonances identifiées sur la carte en fréquence correspondant au second réglage hexapolaire de l’ESRF. Le point de fonctionnement est à l’intersection des deux droites en traits pointillés. La carte en fréquence est repliée sur elle-même (voir aussi Fig. 3.38).
3.40 Exemple de diffusion d’orbites (a) pour le second réglage de l’ESRF. La première orbite (O1) est intégrée sur 1 million de tours ; la particule oscille rapidement transversalement à la résonance
 et lentement longitudinalement. La seconde
orbite (O2) reste piégée 15 000 au voisinage de la résonance
et lentement longitudinalement. La seconde
orbite (O2) reste piégée 15 000 au voisinage de la résonance 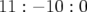 avant de diffuser rapidement dans la zone chaotique de la carte en fréquence.
La variation de ses nombres d’ondes avec le nombre de tours
avant de diffuser rapidement dans la zone chaotique de la carte en fréquence.
La variation de ses nombres d’ondes avec le nombre de tours  est
tracée (b) jusqu’à sa perte au bout de 38 000 tours.
est
tracée (b) jusqu’à sa perte au bout de 38 000 tours. 3.41 Dynamique off momentum pour le second jeu hexapolaire de l’ESRF (colonne 1 :
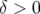 ,
colonne 2 :
,
colonne 2 : 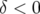 ). Les cartes en fréquence sont profondément modifiées
entre
). Les cartes en fréquence sont profondément modifiées
entre  et
et  (extension spatiale, repliement, résonances).
Pour
(extension spatiale, repliement, résonances).
Pour  , la dynamique est dominée par la résonance d’ordre 5,
, la dynamique est dominée par la résonance d’ordre 5,
 qui est atteinte à des amplitudes de plus en plus
faibles.
qui est atteinte à des amplitudes de plus en plus
faibles. 3.42 Second réglage hexapolaire de l’ESRF : variation de la partie fractionnaire des nombres d’ondes avec l’énergie
 .
. 3.43 Second réglage de l’ESRF : variation de l’ouverture dynamique horizontale avec l’énergie (
 ). Les dimensions sont données par rapport à l’orbite fermée. Elles
sont prises en compte pour le calcul de la durée de vie Touschek en mode
nonlinéaire.
). Les dimensions sont données par rapport à l’orbite fermée. Elles
sont prises en compte pour le calcul de la durée de vie Touschek en mode
nonlinéaire.3.44 Durée de vie Touschek pour le second réglage de l’ESRF en mode multipaquets (a) et faible nombre de paquets (b). Une saturation de la durée de vie est observée pour les calculs en mode nonlinéaire (cercles) par rapport au calcul linéaire (carrés) et donnent des résultats deux fois plus faibles à 12 MV.
3.45 Cartes en fréquence pour le point de fonctionnement historique de l’ESRF pour les deux réglages hexapolaires choisis (a et b). Le point de fonctionnement est beaucoup trop proche des résonances entières : la zone effective de stabilité est petite, l’injection est réalisée au voisinage de résonances et la diffusion des orbites est globalement très élevée.
3.46 Une des douze cellules TBA de l’ALS
3.47 Carte en fréquence (a) et ouverture dynamique (b) calculées pour une maille parfaite de l’ALS pour la surface de section
 (
(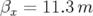 et
et 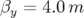 ). La
diffusion permet de nettement distinguer le réseau de résonance sur les deux
figures.
). La
diffusion permet de nettement distinguer le réseau de résonance sur les deux
figures. 3.48 Carte en fréquence de l’ALS sans défaut magnétique avec les principales résonances pour la surface de section
 (
(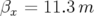 et
et
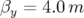 ). Le point de fonctionnement est à l’intersection des lignes en
traits pointillés. Les résonances les plus néfastes pour la dynamique sont
la résonance de couplage 1:-1:0 et la résonance entière
). Le point de fonctionnement est à l’intersection des lignes en
traits pointillés. Les résonances les plus néfastes pour la dynamique sont
la résonance de couplage 1:-1:0 et la résonance entière  qui ne sera
jamais traversée en pratique.
qui ne sera
jamais traversée en pratique. 3.49 Carte en fréquence (a) et ouverture dynamique (b) de l’ALS : maille avec défauts quadripolaires mesurés pour un surface de section en
 (
(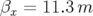 et
et 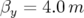 ).
La 12-périodicité de l’anneau est brisée, l’extension spatiale de la carte
en fréquence est réduite d’un facteur 2 dans le plan vertical.
).
La 12-périodicité de l’anneau est brisée, l’extension spatiale de la carte
en fréquence est réduite d’un facteur 2 dans le plan vertical. 3.50 Carte en fréquence (a) et ouverture dynamique (b) de l’ALS (
 et
et
 ) : influence d’un couplage effectif de 1% ajusté à partir des
quadripôles tournés. La diffusion est globalement plus élevée. Seule la
région voisine du point de fonctionnement reste régulière.
) : influence d’un couplage effectif de 1% ajusté à partir des
quadripôles tournés. La diffusion est globalement plus élevée. Seule la
région voisine du point de fonctionnement reste régulière. 3.51 Carte en fréquence de l’ALS avec les erreurs de gradients des quadripôles droits et tournés. Le point de fonctionnement est à l’intersection des lignes en traits pointillés. Des résonances d’ordre 5 non permise par la périodicité sont excitées par les défauts magnétiques, la diffusion est très élevée (cf. zones irrégulières).
3.52 (a) : Variation de la partie fractionnaire des nombres d’ondes de l’ALS en fonction de l’énergie (
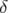 ). (b) : Déplacement du point
de fonctionnement dans le diagramme des résonances tracées jusqu’à l’ordre
7.
). (b) : Déplacement du point
de fonctionnement dans le diagramme des résonances tracées jusqu’à l’ordre
7.3.53 Dynamique off momentum (colonne 1
 , colonne 2
, colonne 2  )
de l’ALS considérée comme machine idéale. Pour
)
de l’ALS considérée comme machine idéale. Pour  la résonance de
couplage 1:-1:0 est atteinte pour des amplitudes de plus en plus faibles.
Ceci est bien confirmé expérimentalement. Les cartes en fréquence ne
présentent pas de repliement, car il n’y a que deux familles d’hexapôles
utilisées pour ajuster les chromaticités.
la résonance de
couplage 1:-1:0 est atteinte pour des amplitudes de plus en plus faibles.
Ceci est bien confirmé expérimentalement. Les cartes en fréquence ne
présentent pas de repliement, car il n’y a que deux familles d’hexapôles
utilisées pour ajuster les chromaticités. 4.1 Cartes en fréquence de l’ALS idéal (à gauche) et en incluant les défauts magnétiques (à droite) tracées pour une surface de Poincaré en
 (
(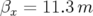 et
et  ).
Les défauts des quadripôles droits et tournés déduits des matrices-réponse
expérimentales brisent la symétrie 12 de l’anneau ; seule la région voisine du
point de fonctionnement reste régulière (Robin, Steier, Laskar et Nadolski,
2000).
).
Les défauts des quadripôles droits et tournés déduits des matrices-réponse
expérimentales brisent la symétrie 12 de l’anneau ; seule la région voisine du
point de fonctionnement reste régulière (Robin, Steier, Laskar et Nadolski,
2000).4.2 Schéma descriptif de la décohérence dans l’espace des phases
 . Au temps
. Au temps 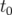 , le faisceau est amorti. Il est déplacé « d’un bloc »
(
, le faisceau est amorti. Il est déplacé « d’un bloc »
(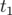 ). Puis, les particules commencent à se déphaser les unes par rapport
aux autres (
). Puis, les particules commencent à se déphaser les unes par rapport
aux autres (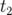 ). Au temps
). Au temps 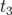 , le faisceau a entièrement « décohéré », les
particules sont répartie dans un anneau autour de la trajectoire de la particule
centrale. La position du centroïde du faisceau est alors nulle.
, le faisceau a entièrement « décohéré », les
particules sont répartie dans un anneau autour de la trajectoire de la particule
centrale. La position du centroïde du faisceau est alors nulle.4.3 Espace des phases (
 ) et schéma pour calculer la fonction de distribution des
particules juste après une impulsion (
) et schéma pour calculer la fonction de distribution des
particules juste après une impulsion ( ) donnée par l’aimant rapide. A
des fins de lisibilité, l’amplitude amortie
) donnée par l’aimant rapide. A
des fins de lisibilité, l’amplitude amortie 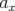 est exagérée.
est exagérée. 4.4 Schéma d’un BPM à quatre électrodes de l’ALS.
4.5 Exemple de signal à faible amplitude (gauche) et grande amplitude (droite) à l’ALS : la décohérence est très rapide, de 600 tours à 100 tours.
4.6 Amplitude du signal (unité arbitraire) en fonction de la tension (kV) sur l’aimant rapide horizontal de l’ALS. Une saturation des BPM et des nonlinéarités apparaissent à partir de 6 000 kV.
4.7 Comparaison d’une carte en fréquence expérimentale (a) avec un modèle numérique de l’ALS incluant les défauts magnétiques mesurés (b) (Robin, Steier, Laskar et Nadolski, 2000).
4.8 Espace des configurations (à gauche) et carte en fréquence expérimentale (à droite) pour le point de fonctionnement d’origine de l’ALS avec mesure expérimentale de la diffusion des orbites (Steier, Robin, Laskar, Nadolski, 2000). Les nœuds de résonances sont nettement observés avec une diffusion rapide à grande amplitude.
4.9 Cartes en fréquence expérimentale (à droite) et simulée (à gauche) de l’ALS pour un point de fonctionnement avec le wiggler W16 fermé. Les défauts de quadripôles droits et tournés sont inclus dans le modèle.
4.10 Cartes en fréquence de l’ALS prenant en compte le wiggler W16, les défauts quadripolaires mesurés et un couplage effectif de 1%.
5.1 Une des quatre mailles de Super-ACO. Les moniteurs de position (BPM) sont situés dans chaque doublet de quadripôles (Q1–Q2) et (Q3–Q4).
5.2 Schéma équivalent d’un quadripôle combiné de Super-ACO. Un quadripôle (
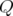 )
contient, en plus du gradient quadripolaire, une lentille décapolaire (
)
contient, en plus du gradient quadripolaire, une lentille décapolaire (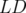 ),
un hexapôle (
),
un hexapôle ( ) et une bobine dipolaire appelée correcteur.
) et une bobine dipolaire appelée correcteur.5.3 Valeurs rms du bruit pour chacun des BPM
 de Super-ACO dans les plans vertical
et horizontal (précision :
de Super-ACO dans les plans vertical
et horizontal (précision : 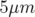 ). Les écarts entre les bruit pour 1 000 et
100 orbites peuvent s’expliquer par le fait que dans un cas les onduleurs sont
fermés et que le courant stocké est différent.
). Les écarts entre les bruit pour 1 000 et
100 orbites peuvent s’expliquer par le fait que dans un cas les onduleurs sont
fermés et que le courant stocké est différent. 5.4 Ecart absolu des dispersions horizontales théorique et mesurée dans les 16 BPM de Super-ACO — hexapôles éteints, onduleurs ouverts —.
5.5 Ecart relatif (en %) par rapport aux valeurs nominales des gradients pour chaque famille quadripolaire de Super-ACO: ces valeurs sont relativement faibles.
5.6 Fonctions
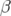 avant
(ligne) et après (étoile) l’ajustement en symétrie 4. L’expérience s’ajuste
parfaitement sur la théorie, car les variations de gradients sont faibles,
de l’ordre du pour mille.
avant
(ligne) et après (étoile) l’ajustement en symétrie 4. L’expérience s’ajuste
parfaitement sur la théorie, car les variations de gradients sont faibles,
de l’ordre du pour mille.5.7 Battement des fonctions
 en conservant
la symétrie 4 de Super-ACO.
en conservant
la symétrie 4 de Super-ACO.5.8 Gains et bruits des BPM et correcteurs de Super-ACO en symétrie 4. Pour un ajustement parfait, les bruits des BPM et correcteurs devraient être voisins de l’unité.
5.9 Ecart relatif (en %) des gradients par rapport aux valeurs nominales pour chacun des 32 quadripôles de Super-ACO. Ces écarts ne sont pas aléatoires : une variation importante du gradient est immédiatement rattrapée sur le quadripôle suivant (e.g. les quadripôles 4 et 5, 8 et 9, 20 et 21, 24 et 25, 27 et 29, 31 et 1).
5.10 Spectre des valeurs singulières obtenu par la méthode SVD. Un seuil apparaît nettement pour
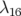 . Au-delà, les valeurs singulières sont
petites, du même ordre de grandeur ; elles correspondent à des paramètres
n’ayant pas un poids significatif dans l’ajustement de la matrice-réponse
de Super-ACO.
. Au-delà, les valeurs singulières sont
petites, du même ordre de grandeur ; elles correspondent à des paramètres
n’ayant pas un poids significatif dans l’ajustement de la matrice-réponse
de Super-ACO.5.11 Ecart relatif (en %) de chacun des gradients des 32 quadripôles de Super-ACO par rapport aux valeurs nominales. Les variations sont de l’ordre du pour mille.
5.12 Ecart relatif (en %) des gradients de chacun des 32 quadripôles de Super-ACO par rapport aux valeurs moyennes obtenues pour les familles. Les variations sont faibles et compatibles en amplitude avec les mesures magnétiques (Barthès et al., 1990).
5.13 Fonctions
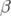 de Super-ACO avant (ligne) et après (étoile)
l’ajustement en brisant la symétrie 4. L’expérience s’ajuste parfaitement
sur la théorie, car les variations de gradients sont faibles, de l’ordre du
pour mille.
de Super-ACO avant (ligne) et après (étoile)
l’ajustement en brisant la symétrie 4. L’expérience s’ajuste parfaitement
sur la théorie, car les variations de gradients sont faibles, de l’ordre du
pour mille.5.14 Battement des fonctions
 en brisant la symétrie 4 de
Super-ACO. Ces variations sont faibles.
en brisant la symétrie 4 de
Super-ACO. Ces variations sont faibles. 5.15 Dispersion horizontale mesurée dans les BPM (carré), ajustée dans les correcteurs (croix) et prédite par LOCO (ligne). L’écart le plus significatif est dans les régions non dispersives de Super-ACO et peut être corrélé avec le facteur d’Amman.
5.16 Gains et bruits de BPM et correcteurs en brisant la symétrie 4 de Super-ACO — hexapôles éteints et onduleurs ouverts — Pour un ajustement parfait, les bruits des BPM et correcteurs devraient être voisins de l’unité.
5.17 Ecarts relatifs entre la fonction dispersion horizontale théorique et mesurée dans les 16 BPM de Super-ACO — hexapôles allumés —.
5.18 Ecarts relatifs des dispersions lorsque les hexapôles sont allumés par rapport au cas où ils sont éteints. Ces écarts relatifs (non tracés) sont plus significatifs dans les régions à faible dispersion de Super-ACO.
5.19 Variation (en %) des gradients quadripolaires de Super-ACO en symétrie 4.
5.20 Gradients quadripolaires créés par l’orbite fermée traversant les hexapôles de Super-ACO.
5.21 Battement des fonctions
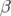 de Super-ACO en symétrie
4 avec hexapôles expérimentaux.
de Super-ACO en symétrie
4 avec hexapôles expérimentaux.5.22 Ecarts relatifs (en %) des gradients de Super-ACO — hexapôles allumés — Une structure 4-périodique semble exister : les variations de gradients sont plus significatives dans les régions dispersives.
5.23 Gradients induits par les hexapôles lorqu’ils ont traversés par une orbite fermée non nulle.
5.24 Orbite fermée (of) horizontale dans les hexapôles déduites des gradients induits par les hexapôles. Les valeurs ne sont pas aléatoires mais reflétent la symétrie 4 de Super-ACO (cf. fonctions
 Fig. 5.25). Il y a aussi une corrélation avec la fonction dispersion mesurée
dans les correcteurs.
Fig. 5.25). Il y a aussi une corrélation avec la fonction dispersion mesurée
dans les correcteurs.5.25 Fonctions
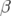 (à gauche) et leurs battements (à
droite) en brisant la symétrie 4 de Super-ACO. L’optique est globalement
peu perturbée.
(à gauche) et leurs battements (à
droite) en brisant la symétrie 4 de Super-ACO. L’optique est globalement
peu perturbée.5.26 Dispersion horizontale mesurée dans les BPM (croix) et ajustée dans les correcteurs (carrés) et prédite par LOCO. L’accord est bon compte tenu des erreurs dipolaires avec une erreur moyenne de 10%.
5.27 Gains et bruits de BPM et correcteurs de Super-ACO — hexapôles allumés, onduleurs ouverts — Pour un ajustement parfait, les bruits des BPM et correcteurs devraient être voisins de l’unité.
5.28 Synoptique de Super-ACO avec les onduleurs SU2, SU3, SU6, SU7 et SU8.
5.29 Ecart entre les dispersions horizontales mesurées dans les BPM de Super-ACO, hexapôles éteints et onduleurs ouverts par rapport au cas hexapôles allumés et onduleurs fermés.
5.30 Ecart entre les dispersions horizontales mesurées dans les BPM de Super-ACO, hexapôles allumés et onduleurs ouverts par rapport au cas hexapôles allumés et onduleurs fermés.
5.31 Valeurs des gradients pour chaque quadripôle, hexapôles allumés et onduleurs fermés. Ces valeurs sont élevées jusqu’à 6% mais on remarque que le code LOCO a compensé localement les glissements des nombres d’ondes induits par les onduleurs.
5.32 Fonctions
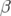 calculées pour une machine théorique avec
le logiciel BETA (ligne) et déduites l’ajustement avec les hexapôles et les
onduleurs fermés (étoile). On observe un bon accord qualitatif avec le modèle
(cf. Brunelle, 1992).
calculées pour une machine théorique avec
le logiciel BETA (ligne) et déduites l’ajustement avec les hexapôles et les
onduleurs fermés (étoile). On observe un bon accord qualitatif avec le modèle
(cf. Brunelle, 1992).5.33 Bump statique dans la section droite SD1 de Super-ACO. Les BPM sont situés dans chaque quadripôle.
5.34 Calibration de l’électrode à 45 degrés en utilisant un bump statique horizontal. L’amplitude effective (carrés) est l’amplitude réellement donnée au faisceau alors que la deuxième courbe (cercles) correspond au signal lu sur les BPM en salle de contrôle de Super-ACO.
5.35 Ecart entre l’amplitude effective et celle lue sur les BPM en salle de contrôle de Super-ACO ; aux grandes amplitudes, les BPM saturent.
5.36 Signal sur le perturbateur P4 entre les tours 125 et 140 pour plusieurs tensions. L’échantillonneur s’est déclenché un tour plus tôt pour les deux premières amplitudes. Un kick a en réalité lieu sur 4 tours de la machine Super-ACO.
5.37 Signal (u.a.) en fonction du nombre de tours pour un kick à x=4.48 mm (faible amplitude) et son spectre de Fourier. La décohérence est faible et le signal peu bruité.
5.38 Signal (u.a.) en fonction du nombre de tours pour un kick à
 kV (grande amplitude) et son spectre de Fourier. La
décohérence est faible et le signal peu bruité.
kV (grande amplitude) et son spectre de Fourier. La
décohérence est faible et le signal peu bruité.5.39 Variation expérimentale (carrés) des nombres d’ondes
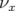 (à gauche) et
(à gauche) et  (à droite) avec
l’amplitude horizontale. Dans chacun des cas, la variation du nombre d’ondes
est quadratique avec l’amplitude.
(à droite) avec
l’amplitude horizontale. Dans chacun des cas, la variation du nombre d’ondes
est quadratique avec l’amplitude.5.40 Variation théorique des nombres d’ondes
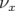 (à gauche) et
(à gauche) et  (à droite) avec l’amplitude horizontale pour
différents modèles de Super-ACO et comparaison à l’expérience (carrés)
: modèle avec les chromaticités expérimentales (triangles), influence des
décapôles (croix), modèle avec les courants mesurés des hexapôles (cercles).
Quelque soit le modèle utilisé, le sens de variation de
(à droite) avec l’amplitude horizontale pour
différents modèles de Super-ACO et comparaison à l’expérience (carrés)
: modèle avec les chromaticités expérimentales (triangles), influence des
décapôles (croix), modèle avec les courants mesurés des hexapôles (cercles).
Quelque soit le modèle utilisé, le sens de variation de  est opposée à
celui mesuré.
est opposée à
celui mesuré.5.41 Différence (étoiles) des nombres d’ondes
 (a) et
(a) et 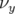 (b) mesurés et prédits par le modèle de Super-ACO. La loi ajustement
(ligne) est dans les deux cas quadratique avec l’amplitude horizontale.
(b) mesurés et prédits par le modèle de Super-ACO. La loi ajustement
(ligne) est dans les deux cas quadratique avec l’amplitude horizontale.
5.42 Variation des nombres d’ondes
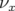 (à gauche) et
(à gauche) et 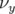 (à droite)
avec l’amplitude
(à droite)
avec l’amplitude  pour différents modèles de Super-ACO incluant une
composante octupolaire. La force des octupôles est proportionnelle à celle
des quadripôles : les facteurs de proportionnalité sont
pour différents modèles de Super-ACO incluant une
composante octupolaire. La force des octupôles est proportionnelle à celle
des quadripôles : les facteurs de proportionnalité sont 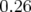 (losanges),
(losanges),
 (croix) et
(croix) et 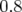 (triangles). Si l’octupôle permet de retrouver le bon
comportement pour
(triangles). Si l’octupôle permet de retrouver le bon
comportement pour 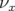 , le désaccord reste grand pour
, le désaccord reste grand pour 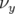 avec la mesure
(carrés).
avec la mesure
(carrés).5.43 Signal (u.a.) sur le perturbateur P6 de Super-ACO entre les tours 125 et 140. Le kick a lieu sur 3 tours consécutifs.
5.44 Comparaison des amplitudes (u.a.) des signaux lus sur les perturbateurs P4 (cercles) et P6 (carrés) en fonction de la tension appliquée. La réponse est dans les deux cas linéaire. Pour que les deux courbes se superposent, il est nécessaire d’introduire un décalage de 0.65 kV (lié à l’étalonnage de la réponse des perturbateur de Super-ACO).
5.45 Comparaison de la variation du nombre d’ondes horizontal expérimental en fonction de l’amplitude : perturbateurs P6 (carrés) et P4 (cercles) de Super-ACO.
5.46 Comparaison de la variation du nombre d’ondes horizontal expérimental en fonction de l’amplitude : perturbateurs P4 (cercles) et P6 (carrés) de Super-ACO avec nouvelle correction.
5.47 Signal (u.a.) sur le perturbateur P4 de Super-ACO entre les tours 125 et 140. L’échantillonneur se déclenche un tour plus tôt pour les trois premières amplitudes. La réponse du perturbateur est une fonction linéaire de la tension appliquée à ses bornes.
5.48 Décohérence du faisceau de Super-ACO en fonction du nombre de tours pour différentes valeurs de kick du perturbateur P4. Le signal (u.a.) présente une décohérence rapide : 500 tours à faible amplitude (4.48 kV) et 100 tours à grande amplitude (11 kV). Au-delà, le signal est noyé dans le bruit.
5.49 Influence des familles d’hexapôles H1 et H2 sur les dimensions de l’ouverture dynamique de Super-ACO — hexapôles allumés : trait continu, éteints : trait pointillé —. Les dimensions réduites d’un facteur deux sont proches de celles mesurées en expérience dans le plan horizontal.
5.50 Variation du nombre d’ondes horizontal
 avec l’amplitude horizontale. Modèles de
Super-ACO avec les chromaticités expérimentales (triangles), les courants
hexapolaires mesurés (cercles). Seule l’introduction de composante
octupolaire précédemment proposée (croix) permet de retrouver la bonne
loi de variation (carrés).
avec l’amplitude horizontale. Modèles de
Super-ACO avec les chromaticités expérimentales (triangles), les courants
hexapolaires mesurés (cercles). Seule l’introduction de composante
octupolaire précédemment proposée (croix) permet de retrouver la bonne
loi de variation (carrés).5.51 Schéma du profil magnétique longitudinal d’un aimant de longueur
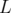 . En approximation hard-edge, le champ
magnétique est constant dans l’élément et nul à l’extérieur. En réalité, le
champ magnétique décroît jusqu’à une valeur nulle de part et d’autre sur
une longueur
. En approximation hard-edge, le champ
magnétique est constant dans l’élément et nul à l’extérieur. En réalité, le
champ magnétique décroît jusqu’à une valeur nulle de part et d’autre sur
une longueur  : on parle de champ de fuite.
: on parle de champ de fuite.5.52 Variation des nombres d’ondes
 et
et  en fonction de l’amplitude horizontale
en fonction de l’amplitude horizontale  . Sans
pseudo-octupôle, le désaccord (cercles) avec la mesure (carrés) est important
(sens de variation opposé pour
. Sans
pseudo-octupôle, le désaccord (cercles) avec la mesure (carrés) est important
(sens de variation opposé pour 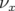 ). L’introduction du pseudo-octupôle
(croix) induit par les champs de fuite des quadripôles de Super-ACO permet
de trouver des glissements des nombres très proches de la mesure dans les
deux plans. Glissements des nombres d’ondes induits : (
). L’introduction du pseudo-octupôle
(croix) induit par les champs de fuite des quadripôles de Super-ACO permet
de trouver des glissements des nombres très proches de la mesure dans les
deux plans. Glissements des nombres d’ondes induits : (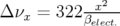 et
et
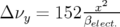 ).
).5.53 Comparaison de la variation des nombres d’ondes
 et
et  en fonction de l’amplitude horizontale. Après ajustement
des pseudo-octupôles de Super-ACO (croix) sur la mesure (carrés), les
accords sont excellents contrairement au modèle sans pseudo-octupôle
(cercles). Glissements des nombres d’ondes induits : (
en fonction de l’amplitude horizontale. Après ajustement
des pseudo-octupôles de Super-ACO (croix) sur la mesure (carrés), les
accords sont excellents contrairement au modèle sans pseudo-octupôle
(cercles). Glissements des nombres d’ondes induits : ( et
et
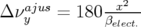 ).
).5.54 Sans composante octupolaire, la carte en fréquence (haut) du point de fonctionnement nominal de Super-ACO est repliée sur elle-même. La demi-ouverture dynamique (bas) associée est importante. La dynamique globale est peu marquée par les résonances, la diffusion est faible.
5.55 Lorsque la composante octupolaire de Super-ACO est modélisée, la dynamique est complètement modifiée : la carte en fréquence (haut) a une grande extension spatiale et présente une diffusion faible. La résonance
 , qui expérimentale détériore la dynamique du faisceau n’est pas
excitée. L’ouverture dynamique (bas) associée reste grande.
, qui expérimentale détériore la dynamique du faisceau n’est pas
excitée. L’ouverture dynamique (bas) associée reste grande.5.56 Lorsque les familles hexapolaires H1 et H2 sont éteintes, la dynamique de Super-ACO modélisé avec la composante octupolaire est altérée : la carte en fréquence modifiée (haut), de nombreuses résonance sont excitées en particulier la résonance
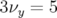 , l’ouverture dynamique verticale (bas) est réduite de
près d’un facteur deux (influence de
, l’ouverture dynamique verticale (bas) est réduite de
près d’un facteur deux (influence de 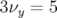 ). L’ouverture dynamique
horizontale est trois fois plus petite. Sur les deux figures, la diffusion est plus
importante au voisinage des résonances.
). L’ouverture dynamique
horizontale est trois fois plus petite. Sur les deux figures, la diffusion est plus
importante au voisinage des résonances.5.57 Pour simuler quelle pourrait être la dynamique réelle de la Super-ACO, la composante octupolaire a été volontairement augmentée pour le point de fonctionnement nominal. Il est frappant de voir combien la dynamique est altérée : carte en fréquence réduite (haut) avec une grande diffusion. L’ouverture dynamique (bas) est constellée de résonance. Une analyse plus détaillée suggère comme nouvelles dimensions :
![[− 15, 0] × [0, 6]](these3004x.png) mm, ce qui serait proche de
l’expérience.
mm, ce qui serait proche de
l’expérience.5.58 Identification des principales résonances de la carte en fréquence 5.57 de Super-ACO. La résonance hexapolaire
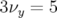 limite la
dynamique dans le plan vertical alors que la résonance
limite la
dynamique dans le plan vertical alors que la résonance  réduit son
extension horizontale.
réduit son
extension horizontale.5.59 Schéma succinct d’un BPM à quatre boutons. Le bouton Haut Extérieur (HE) est utilisé pour réaliser des mesures tour par tour.
5.60 Synoptique de Super-ACO : position des BPM 4 et 12 ainsi que du perturbateur P4.
5.61 Calibration de l’électrode HE du BPM4 de Super-ACO : amplitude du bump statique en fonction du signal normalisé par le courant stocké. Amplitude effective (carrés) et amplitude lues sur les BPM (il y a saturation aux grands amplitude).
5.62 Comparaison entre les valeurs lues en salle de contrôle et celles mesurées pour l’électrode HE du BPM4 de Super-ACO. On observe une caractérisation linéaire, mais aux grandes amplitudes les BPM saturent.
5.63 Exemple de signal (u.a.) en fonction du nombre de tours (a) avec son spectre de Fourier (b) : bump statique de 1 mm. Le niveau de bruit est élevé (pic à 0.25). La fréquence
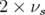 est observée.
est observée.5.64 Calibration de l’électrode HE du BPM12 de Super-ACO : amplitude du bump statique en fonction du signal normalisé par le courant.
5.65 Comparaison entre les valeurs lues en salle de contrôle et mesurées sur l’électrode HE du BPM12 de Super-ACO.
5.66 Signal collecté (u.a.) sur le bouton HE en fonction du nombre de tours pour un kick de 10.87 kV : la décohérence est faible.
5.67 Trajectoire dans le pseudo-espace des phases (
 ). L’épaississement de l’ellipse est
une conséquence de la faible décohérence du faisceau (sur 1 000 tours, cf.
Fig. 5.66).
). L’épaississement de l’ellipse est
une conséquence de la faible décohérence du faisceau (sur 1 000 tours, cf.
Fig. 5.66).5.68 Trajectoire dans l’espace des phases (
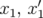 ) : la pente de
l’ellipse est directement reliée au fonctions de Twiss par le facteur
) : la pente de
l’ellipse est directement reliée au fonctions de Twiss par le facteur 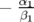 .
L’amplitude est donnée dans le coin supérieur gauche des figures.
.
L’amplitude est donnée dans le coin supérieur gauche des figures.5.69 Espace des phases normalisé pour de faibles amplitudes de kicks : l’épaississement des ellipses provient de la décohérence du faisceau. L’amplitude est donnée dans le coin supérieur gauche des figures.
5.70 Espace des phases normalisé
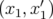 pour de grandes amplitudes : les ellipses sont déformées par les
nonlinéarités. L’amplitude est donnée dans le coin supérieur gauche des
figures.
pour de grandes amplitudes : les ellipses sont déformées par les
nonlinéarités. L’amplitude est donnée dans le coin supérieur gauche des
figures.5.71 Courbe en fréquence
 en fonction de l’amplitude horizontale.
Comparaison entre la mesure (carrés) et différentes modélisations de
Super-ACO : sans composante octupolaire (cercles) et avec pseudo-octupôles
(croix). L’écart subsistant peut être expliqué par l’incertitude sur les
fonctions
en fonction de l’amplitude horizontale.
Comparaison entre la mesure (carrés) et différentes modélisations de
Super-ACO : sans composante octupolaire (cercles) et avec pseudo-octupôles
(croix). L’écart subsistant peut être expliqué par l’incertitude sur les
fonctions  .
.5.72 Signal (u.a.) collecté en fonction du nombre de tours pour un kick de 9.04 kV : la décohérence est un peu plus importante que pour le minimum de couplage.
5.73 Espace des phases normalisé
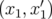 de
Super-ACO pour le point de routine : aux grandes amplitudes les trajectoires
sont fortement déformées par les nonlinéarités. Les ellipses de phases sont
moins nettes que précédemment : c’est la conséquence de l’augmentation
de la décohérence. L’amplitude est donnée dans le coin supérieur gauche de
chaque figure.
de
Super-ACO pour le point de routine : aux grandes amplitudes les trajectoires
sont fortement déformées par les nonlinéarités. Les ellipses de phases sont
moins nettes que précédemment : c’est la conséquence de l’augmentation
de la décohérence. L’amplitude est donnée dans le coin supérieur gauche de
chaque figure.5.74 Courbes en fréquence
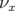 (à gauche) et
(à gauche) et 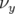 (à droite) en
fonction de l’amplitude horizontale. Comparaison entre la mesure (carrés)
et différents modèles de Super-ACO : sans composante octupolaire (cercles)
et avec pseudo-octupôles (croix). Le modèle avec les pseudo-octupôles
donne un bon accord avec la mesure.
(à droite) en
fonction de l’amplitude horizontale. Comparaison entre la mesure (carrés)
et différents modèles de Super-ACO : sans composante octupolaire (cercles)
et avec pseudo-octupôles (croix). Le modèle avec les pseudo-octupôles
donne un bon accord avec la mesure.5.75 Signal (u.a.) collecté en fonction du nombres de tours pour un kick de 6.53 kV : la décohérence a lieu sur 150 tours. Au-delà, le signal est noyé dans le bruit.
5.76 Espace des phases normalisé
 de Super-ACO lorsque les familles hexapolaires H1 et
H2 sont éteintes en réalisant le minimum de couplage : la décohérence est
d’autant plus rapide que la tension du perturbateur est élevé (trajectoires
de plus en plus spiralées dans l’espace des phases). L’amplitude initiale du
signal est donné dans le coin supérieur gauche de chaque figure.
de Super-ACO lorsque les familles hexapolaires H1 et
H2 sont éteintes en réalisant le minimum de couplage : la décohérence est
d’autant plus rapide que la tension du perturbateur est élevé (trajectoires
de plus en plus spiralées dans l’espace des phases). L’amplitude initiale du
signal est donné dans le coin supérieur gauche de chaque figure.5.77 Courbe en fréquence
 en fonction de l’amplitude horizontale : familles
hexapolaires H1 et H2 éteintes avec minimum de couplage. Comparaison
entre la mesure (carrés) et différentes modélisations de Super-ACO :
sans composante octupolaire (cercles) et avec pseudo-octupôles (croix).
Le modèle avec les pseudo-octupôles donne un accord remarquable avec
la mesure.
en fonction de l’amplitude horizontale : familles
hexapolaires H1 et H2 éteintes avec minimum de couplage. Comparaison
entre la mesure (carrés) et différentes modélisations de Super-ACO :
sans composante octupolaire (cercles) et avec pseudo-octupôles (croix).
Le modèle avec les pseudo-octupôles donne un accord remarquable avec
la mesure.5.78 Signal collecté pour un kick de 5.92 kV : la décohérence est très rapide (200 tours).
5.79 Espace des phases normalisé
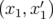 de Super-ACO lorsque les familles H1 et H2 sont éteintes. La présence de
couplage diminue les dimensions de l’ouverture dynamique et accélère le
phénomène de décohérence. L’amplitude initiale du signal est donnée dans
le coin supérieur gauche de chaque figure.
de Super-ACO lorsque les familles H1 et H2 sont éteintes. La présence de
couplage diminue les dimensions de l’ouverture dynamique et accélère le
phénomène de décohérence. L’amplitude initiale du signal est donnée dans
le coin supérieur gauche de chaque figure.5.80 Courbes en fréquence
 (à
gauche) et
(à
gauche) et 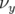 (à droite) en fonction de l’amplitude horizontale : familles
hexapolaires H1 et H2 éteintes sans minimum de couplage. Comparaison
entre la mesure (carrés) et différentes modélisations de Super-ACO :
sans composante octupolaire (cercles) et avec pseudo-octupôles (croix).
Le modèle avec les pseudo-octupôles donne un bon accord bon le nombre
d’ondes horizontal.
(à droite) en fonction de l’amplitude horizontale : familles
hexapolaires H1 et H2 éteintes sans minimum de couplage. Comparaison
entre la mesure (carrés) et différentes modélisations de Super-ACO :
sans composante octupolaire (cercles) et avec pseudo-octupôles (croix).
Le modèle avec les pseudo-octupôles donne un bon accord bon le nombre
d’ondes horizontal.A.1 Schéma illustrant la rotation d’un angle
 d’un
élément rectiligne — inspiré de Forest, 1998 —
d’un
élément rectiligne — inspiré de Forest, 1998 —B.1 Carte en fréquence (haut) et ouverture dynamique (bas) de l’optique faible émittance numéro 1 de SOLEIL (
 m et
m et  m). L’ouverture dynamique est
grande. Elle est marquée par les résonances ; en particulier, la protubérance
observée vers
m). L’ouverture dynamique est
grande. Elle est marquée par les résonances ; en particulier, la protubérance
observée vers  mm correspond à la résonance d’ordre 9. La
diffusion est faible au voisinage du point de fonctionnement (vert), plus
importante au voisinage des résonances et élevée sur le bord de l’ouverture
dynamique (rouge).
mm correspond à la résonance d’ordre 9. La
diffusion est faible au voisinage du point de fonctionnement (vert), plus
importante au voisinage des résonances et élevée sur le bord de l’ouverture
dynamique (rouge).B.2 Carte en fréquence et ouverture dynamique pour une surface de Poincaré en
 (
( m et
m et 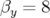 m) pour
l’optique 1 modifiée de SOLEIL. L’ouverture dynamique est presque aussi
grande que pour la première optique ; la carte en fréquence est repliée sur
elle-même : sa lecture en est rendue plus difficile. Son extension spatiale
est réduite, moins de résonances sont rencontrées. La diffusion des
orbites est globalement plus faible.
m) pour
l’optique 1 modifiée de SOLEIL. L’ouverture dynamique est presque aussi
grande que pour la première optique ; la carte en fréquence est repliée sur
elle-même : sa lecture en est rendue plus difficile. Son extension spatiale
est réduite, moins de résonances sont rencontrées. La diffusion des
orbites est globalement plus faible. B.3 Haut : Carte en fréquence tracée pour le premier (
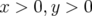 ) et second (
) et second ( ) quadrant de
l’ouverture dynamique. Super-ACO est modélisé comme machine idéale.
Bas : Ouverture dynamique associée (
) quadrant de
l’ouverture dynamique. Super-ACO est modélisé comme machine idéale.
Bas : Ouverture dynamique associée ( m et
m et 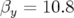 m). Le
point de fonctionnement est le coin supérieur droit de la carte (origine de
l’ouverture dynamique). La dynamique est principalement dominée par la
résonance d’ordre 3
m). Le
point de fonctionnement est le coin supérieur droit de la carte (origine de
l’ouverture dynamique). La dynamique est principalement dominée par la
résonance d’ordre 3  qui donne la limite verticale
de l’ouverture dynamique (
qui donne la limite verticale
de l’ouverture dynamique ( mm). Toute la partie
mm). Toute la partie 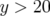 mm sur
l’ouverture dynamique correspond à l’île de cette résonance : au centre la
diffusion est faible (vert), car les particules sont capturée par la résonance
et y restent ; sur les bords (régions hyperboliques)la diffusion est élevée
(orange-rouge).
mm sur
l’ouverture dynamique correspond à l’île de cette résonance : au centre la
diffusion est faible (vert), car les particules sont capturée par la résonance
et y restent ; sur les bords (régions hyperboliques)la diffusion est élevée
(orange-rouge). B.4 Carte en fréquence (haut) et ouverture dynamique (bas) calculées en incluant dans le modèle de Super-ACO les mesures magnétiques des quadripôles droits (
 m et
m et  m). La diffusion est
globalement plus élevée, les largeurs de résonances plus grandes. L’influence
des défauts magnétiques reste faible (mêmes dimensions de l’ouverture
dynamique).
m). La diffusion est
globalement plus élevée, les largeurs de résonances plus grandes. L’influence
des défauts magnétiques reste faible (mêmes dimensions de l’ouverture
dynamique). B.5 Super-ACO deuxième quadrant (
 ) : carte en
fréquence et ouverture dynamique pour le point de fonctionnement nominal
(
) : carte en
fréquence et ouverture dynamique pour le point de fonctionnement nominal
( m et
m et 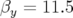 m). La carte en fréquence est très compacte
: peu de résonances sont rencontrées. Il est difficile de comprendre avec
cette modélisation les observations expérimentales.
m). La carte en fréquence est très compacte
: peu de résonances sont rencontrées. Il est difficile de comprendre avec
cette modélisation les observations expérimentales. B.6 Sans composante octupolaire, la carte en fréquence de Super-ACO (haut) est repliée sur elle-même. L’ouverture dynamique (bas) est grande, la dynamique est peu marquée par les résonances.
B.7 Avec composante octupolaire, la dynamique de Super-ACO est complètement modifiée : grande extension spatiale de la carte en fréquence (haut) mais ouverture dynamique (bas) plus grande.
B.8 Avec composante octupolaire, familles hexapolaires H1 et H2 éteintes : la dynamique de Super-ACO est altérée : carte en fréquence modifiée (haut), ouverture dynamique verticale (bas) réduite de près d’un facteur deux (cf. Fig. B.7).
B.9 Composante octupolaire surestimée : la dynamique de Super-ACO est fortement altérée, carte en fréquence tronquée (haut) avec une grande diffusion et l’ouverture dynamique (bas) réduite dans les deux plans (cf. Fig. B.7).
B.10 Carte en fréquence (haut) et ouverture dynamique (bas) : premier jeu hexapolaire de l’ESRF pour une surface de section en
 (
(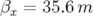 et
et  ). La
dynamique est dominée par la résonance de couplage 3:-2:0 et la résonance
entière
). La
dynamique est dominée par la résonance de couplage 3:-2:0 et la résonance
entière  . Les zones elliptiques et hyperboliques associées sont
nettement identifiables sur l’ouverture dynamique.
. Les zones elliptiques et hyperboliques associées sont
nettement identifiables sur l’ouverture dynamique. B.11 Carte en fréquence et ouverture dynamique pour le second réglage de l’ESRF hexapolaire calculée pour une surface de section à
 (
(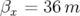 et
et 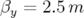 ).
La dynamique est dominée par la résonance
).
La dynamique est dominée par la résonance  atteinte à grande amplitude.
atteinte à grande amplitude. B.12 Carte en fréquence (haut) et ouverture dynamique (bas) calculées pour une maille parfaite de l’ALS pour une surface de Poincaré en
 (
( et
et  ). La diffusion
permet de nettement distinguer le réseau de résonance sur les deux figures.
). La diffusion
permet de nettement distinguer le réseau de résonance sur les deux figures.
B.13 Carte en fréquence et ouverture dynamique : maille avec défauts quadripolaires mesurés pour un surface de section en
 (
( et
et 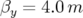 ). La 12-périodicité de l’ALS est brisée, l’extension spatiale
de la carte en fréquence est réduite d’un facteur 2 dans le plan vertical.
). La 12-périodicité de l’ALS est brisée, l’extension spatiale
de la carte en fréquence est réduite d’un facteur 2 dans le plan vertical.
B.14 Carte en fréquence (a) et ouverture dynamique (b) de l’ALS (
 et
et 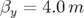 ) : influence du couplage de 1% ajusté à partir
d’une distribution de quadripôles tournés. La diffusion est globalement plus
élevée. Seule la région voisine du point de fonctionnement reste régulière.
) : influence du couplage de 1% ajusté à partir
d’une distribution de quadripôles tournés. La diffusion est globalement plus
élevée. Seule la région voisine du point de fonctionnement reste régulière.
B.15 Espace des configurations et carte en fréquence expérimentale pour un point de fonctionnement antérieur avec mesure expérimentale de la diffusion des orbites (Steier, Robin, Laskar, Nadolski, 2000).